1 #include<iostream>
2 #include <cstdlib>
3 #include <ctime>
4 #include <string>
5 using namespace std;
6 /*
7 *对于多项式的,我们可以用一个二进制数来表示进行减法
8 *例如:x^3+x+1 可以以二进制数1011来表示,即十进制数的11
9 *本题给定既约多项式 x^8+x^4+x^3+x+1 可以通过用二进制数100011011来表示
10 *即十进制数283
11 *因此其生成的有限域GF(2^8)/(x^8+x^4+x^3+x+1),共有2^8=256个元素
12 */
13
14 //定义一些常量
15 const int M = 283; //x^8+x^4+x^3+x+1
16 const int p = 2; //模2
17 const int N = 256; //有限域内的元素个数
18
19 int a,b; //在有限域内选取的两个元素
20
21 int remainvalue; //余数式
22 int x,y;
23
24 class GFpn
25 {
26 public:
27 //在有限域内部随机选取两个元素
28 void random_element();
29
30 //返回一个十进制数的二进制数的最高位
31 int index_of_binary_max(int value);
32
33 //将一个十进制数转化为对应的多项式字符串
34 string value_into_polynomial(int value);
35
36 //求一个数的2次幂,即返回2^value.
37 int power_of_value(int value);
38
39 //返回多项式的除法,remainvalue为余数
40 int divide(int a,int b,int &remainvalue);
41
42 //相当于ax - q * bx 在多项式异或的范畴下
43 //三元组运算
44 int Tx(int ax,int q,int bx);
45
46 //扩展的欧几里得算法
47 //其中x返回的是b mod m的多项式的乘法逆元
48 //所对应的的十进制数表达式
49 int extent_gcd(int m,int b,int &x,int &y);
50
51 //定义多项式有限域内的加法运算
52 //实际上是两个数的异或
53 int polynomial_add(int a,int b);
54
55 //定义多项式有限域内的减法运算
56 //实际上也是两个数的异或
57 int polynomial_sub(int a,int b);
58
59 //定义多项式有限域内的乘法运算
60 //通过移位,来实现逐位异或
61 int polynomial_mul(int a,int b);
62
63 //定义多项式的除法运算
64 //实质上也是乘以多项式在有限域的逆元
65 int polynomial_div(int a,int b);
66 };
67
68 //在有限域中随机选取两个元素
69 //等价为在0——N-1中随机选取两个数
70 void GFpn::random_element()
71 {
72 a = rand() % N;
73 b = rand() % N;
74 }
75
76
77 //求数的二进制数的最高位
78 int GFpn::index_of_binary_max(int value)
79 {
80 int tmp = 1;
81 int count = 0;
82 int i;
83 for(i = 0;i < sizeof(int) * 8;i++)
84 {
85 if(value & tmp)
86 count = i;
87 tmp = tmp * 2;
88 }
89 return count;
90 }
91
92 //将一个数转化为多项式
93 //如:11——>1011——>x^3+x+1
94 string GFpn::value_into_polynomial(int value)
95 {
96 string result;
97 int i;
98 int tmp = 1;
99 int flag = 0;
100 int c = index_of_binary_max(value);
101 for(i = 0;i < sizeof(int) * 8;i++)
102 {
103 if(value & tmp)
104 {
105 if(i == 0)
106 {
107 result += "1";
108 }
109 else if(i == 1)
110 {
111 result += "x";
112 }
113 else
114 {
115 result += "x^";
116 result += '0'+ i;
117 }
118 flag = 1;
119 if(i < c)
120 result += "+";
121 }
122 tmp = tmp * 2;
123 }
124 if(flag == 0)
125 result += "0";
126 return result;
127 }
128
129 //求一个数的2次幂,即返回2^value.
130 int GFpn::power_of_value(int value)
131 {
132 return 1 << (value);
133 }
134
135
136 //返回多项式的除法,remainvalue为余数
137 int GFpn::divide(int a,int b,int &remainvalue)
138 {
139 int aindex = index_of_binary_max(a);
140 int bindex = index_of_binary_max(b);
141 if(aindex < bindex)
142 {
143 remainvalue = a;
144 return 0;
145 }
146 int c = aindex - bindex;
147 int tmp = b;
148 tmp = tmp << c;
149 a = a ^ tmp;
150 return power_of_value(c) | divide(a,b,remainvalue);
151 }
152
153
154 //相当于ax - q * bx 在多项式异或的范畴下
155 //三元组运算
156 int GFpn::Tx(int ax,int q,int bx)
157 {
158 int tmp = 1;
159 int value = 0;
160 int i;
161 for(i = 0;i < sizeof(int) * 8;i++)
162 {
163 if(q & tmp)
164 {
165 value = value ^ (bx << i);
166 }
167 tmp = tmp * 2;
168 }
169 return ax ^ value;
170 }
171
172
173 //扩展的欧几里得算法
174 int GFpn::extent_gcd(int m,int b,int &x,int &y)
175 {
176 //先定义(a1,a2,a3)三元组
177 int a1 = 1,a2 = 0,a3 = m;
178 //再定义(b1,b2,b3)三元组
179 int b1 = 0,b2 = 1,b3 = b;
180 int remainvalue=0;
181 while(1)
182 {
183 if(b3==0)
184 return a3;
185 if(b3==1)
186 return b3;
187 int q = divide(a3,b3,remainvalue);
188 //分别定义(t1,t2,t3)三元组
189 int t1 = Tx(a1,q,b1); //q = a3 / b3;(多项式范畴下)
190 int t2 = Tx(a2,q,b2); //t1<——a1 - q * b1
191 int t3 = remainvalue; //t2<——a2 - q * b2
192 //迭代过程
193 //(a1,a2,a3)<——(b1,b2,b3)
194 a1 = b1;a2 = b2;a3 = b3;
195 //(b1,b2,b3)<——(t1,t2,t3)
196 b1 = t1;b2 = t2;b3 = t3;
197 x = b2;
198 y = b3;
199 }
200 }
201
202 //定义多项式有限域内的加法运算
203 //实际上是两个数的异或
204 int GFpn::polynomial_add(int a,int b)
205 {
206 int result;
207 result = a ^ b;
208 return result;
209 }
210
211 //定义多项式有限域内的减法运算
212 //实际上也是两个数的异或
213 int GFpn::polynomial_sub(int a,int b)
214 {
215 int result;
216 result = a ^ b;
217 return result;
218 }
219
220 //定义多项式有限域内的乘法运算
221 //通过移位,来实现逐位异或
222 int GFpn::polynomial_mul(int a,int b)
223 {
224 int result = 0;
225 int remain = 0;
226 int num = index_of_binary_max(b);
227 int i;
228 for(i = 0;i < num;i++)
229 {
230 if(b & 1)
231 {
232 result ^= a;
233 }
234 a <<= 1;
235 b >>= 1;
236 }
237 result ^= a;
238 result = divide(result,M,remain);
239 return remain;
240 }
241
242 //定义多项式的除法运算
243 //实质上也是乘以多项式在有限域的逆元
244 int GFpn::polynomial_div(int a,int b)
245 {
246 int result;
247 int aa = 0,bb = 0;
248 int div_result = extent_gcd(M,b,aa,bb);
249 result = polynomial_mul(a,aa);
250 return result;
251 }
252
253 int main()
254 {
255 GFpn gg;
256 //srand()函数产生一个以当前时间开始的随机种子.以保证每次产生的随机数矩阵都不相同
257 srand((unsigned)time(0));
258 cout << "给定多项式: " << gg.value_into_polynomial(M) << endl;
259 cout << endl << "生成有限域......" << endl;
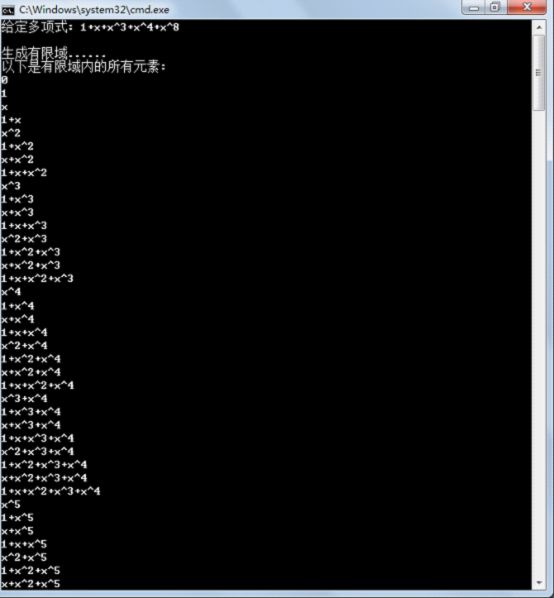
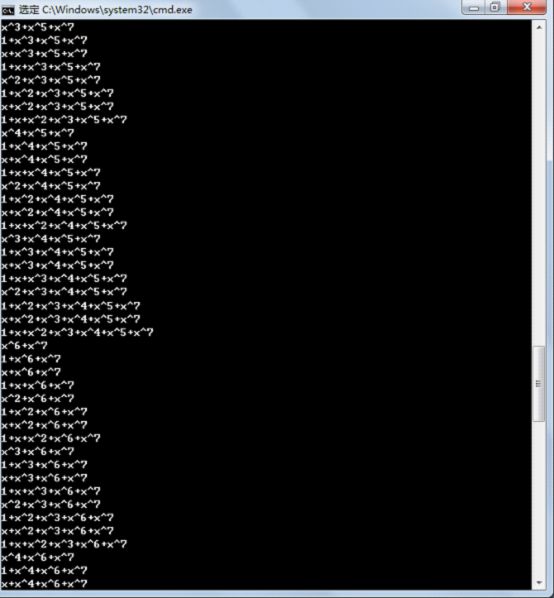
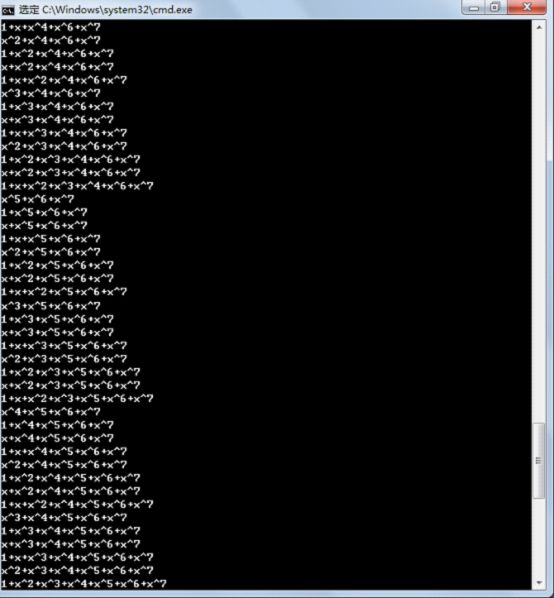
260 cout << "以下是有限域内的所有元素:"<< endl;
261 int i;
262 for(i = 0;i < N;i++)
263 cout << gg.value_into_polynomial(i) << endl;
264 cout << endl;
265 cout << "先从所构造的有限域中随机选取两个元素,分别为:" << endl;
266 gg.random_element();
267 cout << gg.value_into_polynomial(a) << " 和 " << gg.value_into_polynomial(b) << endl;
268 cout << endl << "分别进行加减乘除运算:" << endl;
269 cout << "加:" << "(" << gg.value_into_polynomial(a) << ") + (" << gg.value_into_polynomial(b) << ") = "
270 << gg.value_into_polynomial(gg.polynomial_add(a,b)) << endl;
271 cout << endl;
272 cout << "减:" << "(" << gg.value_into_polynomial(a) << ") - (" << gg.value_into_polynomial(b) << ") = "
273 << gg.value_into_polynomial(gg.polynomial_sub(a,b)) << endl;
274 cout << endl;
275 cout << "乘:" << "(" << gg.value_into_polynomial(a) << ") * (" << gg.value_into_polynomial(b) << ") = "
276 << gg.value_into_polynomial(gg.polynomial_mul(a,b)) << endl;
277 cout << endl;
278 cout << "除:" << "(" << gg.value_into_polynomial(a) << ") / (" << gg.value_into_polynomial(b) << ") = "
279 << gg.value_into_polynomial(gg.polynomial_div(a,b)) << endl;
280 cout << endl;
281 int a;
282 cout << "是否还要继续:(按1退出)(按2继续)?" << endl;
283
284 while(cin >> a && a != 1)
285 {
286 cout << "先从所构造的有限域中随机选取两个元素,分别为:" << endl;
287 gg.random_element();
288 cout << gg.value_into_polynomial(a) << " 和 " << gg.value_into_polynomial(b) << endl;
289 cout << endl << "分别进行加减乘除运算:" << endl;
290 cout << "加:" << "(" << gg.value_into_polynomial(a) << ") + (" << gg.value_into_polynomial(b) << ") = "
291 << gg.value_into_polynomial(gg.polynomial_add(a,b)) << endl;
292 cout << endl;
293 cout << "减:" << "(" << gg.value_into_polynomial(a) << ") - (" << gg.value_into_polynomial(b) << ") = "
294 << gg.value_into_polynomial(gg.polynomial_sub(a,b)) << endl;
295 cout << endl;
296 cout << "乘:" << "(" << gg.value_into_polynomial(a) << ") * (" << gg.value_into_polynomial(b) << ") = "
297 << gg.value_into_polynomial(gg.polynomial_mul(a,b)) << endl;
298 cout << endl;
299 cout << "除:" << "(" << gg.value_into_polynomial(a) << ") / (" << gg.value_into_polynomial(b) << ") = "
300 << gg.value_into_polynomial(gg.polynomial_div(a,b)) << endl;
301 cout << endl;
302 cout << "是否还要继续:(按1退出)(按2继续)?" << endl;
303 }
304 return 0;
305 }