codeforces A. Distance and Axis

题目

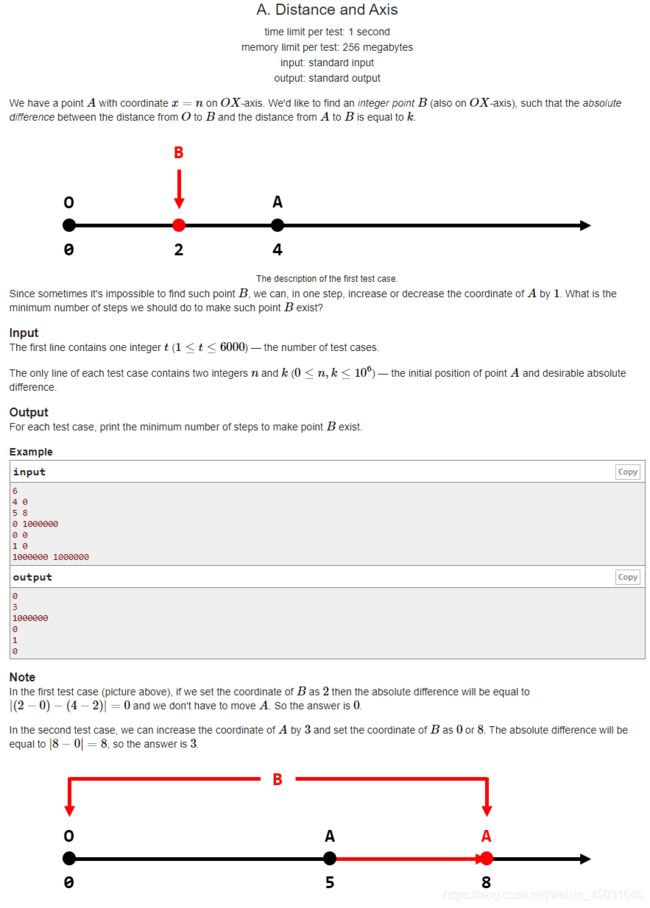
题意：

给你两个整数$n,k$，其中$A$点刚开始的坐标为$n$，现在你要保证$|(B-0)-(A-B)|=k$，问$B$的坐标是多少。

思路：

我们将公式化简一下可以得到$|2\ast B-A|=k$，我们假设$A\ge 2\ast B$，那么就有$(A-k)/2=B$即$(n-k)/2=B$，所以当$n<k$时，$B$为负数，这是不允许的，所以$ans=k-n$，当$(n-k)\%2\ne 0$的时候，那么我们只要$n+1$就可以满足$(n-k)\%2=0$

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
typedef long long ll;
typedef vector<int> veci;
typedef vector<ll> vecl;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
template <class T>
inline void read(T &ret) {
    char c;
    int sgn;
    if (c = getchar(), c == EOF) return ;
    while (c != '-' && (c < '0' || c > '9')) c = getchar();
    sgn = (c == '-') ? -1:1;
    ret = (c == '-') ? 0:(c - '0');
    while (c = getchar(), c >= '0' && c <= '9') ret = ret * 10 + (c - '0');
    ret *= sgn;
    return ;
}
inline void outi(int x) {if (x > 9) outi(x / 10);putchar(x % 10 + '0');}
inline void outl(ll x) {if (x > 9) outl(x / 10);putchar(x % 10 + '0');}
int main() {
    int t; read(t); while (t--) {
        int n, k; read(n), read(k);
        if (n < k) printf("%d\n", k - n);
        else if ((n - k) % 2 == 0) printf("0\n");
        else printf("1\n");
    }
    return 0;
}