fft 最终版
FFT 快速傅里叶变换
这是求多项式乘积系数的算法:
例如:
F(x) = a0+a1x+a2x2;
G(x) = b0+b1x+b2x2;
T(x) = F(x)*G(x) = c0+c1x+c2x2;
我们求的就是T(x) 的系数
这里引入了点值表示法和系数表示法
因为2个点可以确定1元二次方程
同理n个点就可以确定1元n此方程
FFT 就是做的就是快速的做到
系数表示法转点值表示法 and 点值表示法转系数表示法
当我们求出了f(x) 对应的n个点和同样x 的n个G(x)
相乘就可以的出n个T(x) 的点值
具体学习可以看这里
单位根的一些性质
推FFT的过程中需要用到ω的一些性质
ωnk=ω 2n2k
ωn^k+ 2n^ =−ωnk
复数模板
struct co {
double x, y;
co(){}
co (double xx, double yy):x(xx),y(yy) {}
co operator+(const co &a) const {
return co(x+a.x, y+a.y);
}
co operator-(const co &a) const {
return co(x-a.x, y-a.y);
}
co operator*(const co &a) const {
return co(x*a.x-y*a.y, x*a.y+a.x*y);
}
} a[mx], b[mx];
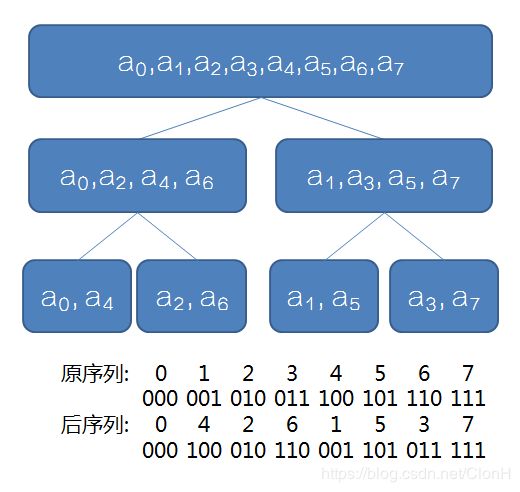
递归版
void Fft(co *a, int n, int type) { ///递归版
if (n == 1) return;
int n1 = n>>1;
co a1[n1], a2[n1];
for (int i = 0; i < n1; ++i)
a1[i] = a[i<<1], a2[i] = a[i<<1|1];
Fft(a1, n1, type);
Fft(a2, n1, type);
co wn(cos(2.0*pi/n), type*sin(2.0*pi/n)), w(1, 0);
for (int i = 0; i < n1; ++i, w = w*wn) {
co t = w*a2[i];
a[i] = a1[i]+t, a[i+n1] = a1[i]-t;
/// A[w i/n] = A1[w i/n/2]+w i/n A2[w i/n/2]; -w i/n A2[w i/n/2];
}
return;
}
迭代版
int r[mx];
void fft(co *a, int n, int type) {
for (int i = 0; i < n; ++i) if (i < r[i]) swap(a[i], a[r[i]]);
for (int i = 2; i <= n; i<<=1) {
co wn(cos(2*pi/i), type*sin(2*pi/i));
for (int j = 0; j < n; j += i) {
co w(1, 0);
int mit = i>>1;
for (int z = 0; z < mit; ++z, w = w*wn) {
co x = a[j+z], y = w*a[j+mit+z];
a[j+z] = x+y;
a[j+mit+z] = x-y;
}
}
}
return;
}
main()
while (as<=n+m) as<<=1, l++;
for (int i = 0; i < as; ++i)
r[i] = ( r[i >> 1] >> 1 ) | ( (i & 1) << (l - 1));
int main() {
int n, m, as = 1;
int l = 0;
n = read(), m = read();
while (as<=n+m) as<<=1, l++;
for (int i = 0; i < as; ++i)
r[i] = ( r[i >> 1] >> 1 ) | ( (i & 1) << (l - 1));
for (int i = 0; i <= n; ++i) a[i].x = read();
for (int i = 0; i <= m; ++i) b[i].x = read();
fft(a, as, 1); fft(b, as, 1);
for (int i = 0; i <= as; ++i)
a[i] = a[i]*b[i];
fft(a, as, -1);
for (int i = 0; i <= n+m; ++i)
printf("%d ", (int)(a[i].x/as+0.5));
}