数据的处理与分析-正态分布,and so on!
1 satas包的介绍
- 分布的密度分布函数,累计分布函数,残存函数,分位点函数,逆残存函数
- 分布的统计量:均值,方差,峰度,偏度,矩
- 分布的线性变换生成
- 数据的分布拟合
- 分布构造
- 描述统计
- t检验,ks检验,卡方检验,正态性检,同分布检验
- 核密度估计(从样本估计概率密度分布函数)
-
from scipy import stats # 有关统计的包
from scipy import optimize
import numpy as np #数据生成处理
import random
import matplotlib.pyplot as plt #画图
import seaborn as sns
2 start
x = np.array([0,1]) # 新建一个向量
print(np.mean(x))
print(np.min(x))
print(np.max(x))
print(np.var(x))
print(np.std(x))
print('sample var',x.var(ddof=1))#样本方差 /n-1
print(x.std(ddof=1))#样本标准差
random.seed(123456789) #设置一个随机种子,使得每次生成的数字相同。
random.random()#产生一个在0-1之间的数字
random.randint(0,10)#【0-10)之间生成一个整数
np.random.randint(low=10,high=20,size=(1,2)) 【10,20)之间产生一个一行两列的数组。
#rand 生成均匀分布的伪随机数。分布在(0~1)之间
np.random.rand(1,2,3)
#randn 生成标准正态分布的伪随机数(均值为0,方差为1)
np.random.randn(2,3)
3 图示分析
sns.set(style="whitegrid")
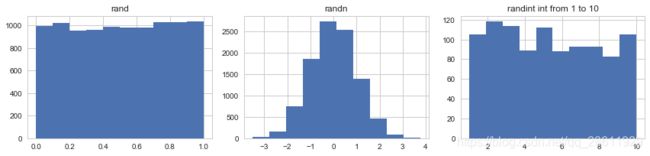
fig,axes = plt.subplots(1,3,figsize=(12,3))#一行三列
axes[0].hist(np.random.rand(10000))
axes[0].set_title('rand')
axes[1].hist(np.random.randn(10000))
axes[1].set_title('randn')
axes[2].hist(np.random.randint(1,11,1000))
axes[2].set_title('randint int from 1 to 10')
fig.tight_layout()
prng = np.random.RandomState(123456789) # 定义局部种子
prng.rand(2, 4)#正太分布
prng.chisquare(2,size=(2,2))#卡方分布
prng.standard_t(1, size=(2, 3)) # t 分布
prng.f(5, 2, size=(2, 4)) # F 分布
prng.binomial(10, 0.5, size=10) # 二项分布
prng.poisson(5, size=10) # 泊松分布
X = stats.norm(1, 0.5) # 定义一个正态分布,期望是 1,标准差是 0.5
print(type(X)) # 可以看出 X 其实是个分布
print(X.mean()) # 期望
print(X.median()) # 中位数
print(X.std()) # 标准差
print(X.var()) # 方差
print([X.moment(n) for n in range(5)]) # 计算各阶中心矩,下面会详细介绍
print(X.stats()) # 打印统计量
print(X.pdf([0, 1, 2])) # 概率密度函数 pdf,给定 x 值,给出密度函数的 y 值
print(X.cdf([0, 1, 2])) # 累积概率函数,其实是 pdf 积分,也就是密度曲线下的面积,整个的面积为 1
print(X.rvs(10))# 用于生成随机数,跟前面 random 模块功能类似
print(X.interval(0.95)) # 整个函数比较有用,计算曲线下面积为 0.95 时对应的两个 x 值
print(X.dist)
1.0
1.0
0.5
0.25
[1.0, 1.0, 1.25, 1.75, 2.6875]
(array(1.), array(0.25))
[0.10798193 0.79788456 0.10798193]
[0.02275013 0.5 0.97724987]
[1.15981261 0.72885402 0.76682503 1.18474284 0.83671076 1.56853954
0.13431861 0.37365665 0.99048727 1.4256104 ]
(0.020018007729972975, 1.979981992270027)
4检验以及画图
- 在这,np帮助我们随机生成一个正太分布,LOOK!import numpy as np
from matplotlib.pyplot as plt
np.random.seed(123456789)
mu, sigma = 0, 1
X = stats.norm(mu-0.2, sigma)
n = 1000
X_samples = X.rvs(n)
plt.hist(X_samples)
在这里呢,我们介绍一下T检验!
小插曲,开始。
均值比较T,方差比较F.
一是正态性、二是方差齐性。
T检验的条件:要比较的数据必须是计量数据(连续)而非计数数据(离散),组别为2组,2组以上则是做方差分析。
t检验通常需要做一个方差齐性检验。
方差齐性检验(test for homogeneity of variance),假设检验的一种。关于两个或两个以上总体的方差是否相等的统计检验。根据情况不同,有不同的检验方法。在两个总体相互独立且服从正态时,可用F检验;在k个(k>2)总体相互独立且服从正态时,可用Bartlett检验。
单一T检验:数据的均值与一个数据有误差异。
配对T检验:一组数据在处理前后有误差异。(有米有服药前后的差异性)
独立样本t检验:用来看两组数据的平均值有无差异性。
1 单一T检验
stats.ttest_1samp(X_samples, mu)
Ttest_1sampResult(statistic=-0.5105076928402886, pvalue=0.6098086085372822)p>0.05,不能拒绝原假设H0,无差异。
2 配对T检验:
mu1, mu2 = np.random.rand(2) # 随机产生两个不同的参数
print(mu1,mu2)
X1 = stats.norm(mu1, sigma) # 标准差一样
X1_sample = X1.rvs(n) # 生成第 1 组数据
X2 = stats.norm(mu2, sigma)
X2_sample = X2.rvs(n) # 生成第 2 组数据
t, p = stats.ttest_ind(X1_sample, X2_sample) # 两样本 T 检验
print(t)
print(p)# p 值太小,可以拒绝原假设
0.9260949986224181 0.32866025468899795
13.486620740890883
9.716360485026744e-40X1 = stats.norm(0.1, sigma) # 标准差一样
X1_sample = X1.rvs(n) # 生成第 1 组数据
X2 = stats.norm(0.15, sigma)
X2_sample = X2.rvs(n) # 生成第 2 组数据
t, p = stats.ttest_ind(X1_sample, X2_sample) # 两样本 T 检验
print(t)
print(p)#
-1.654618194962103
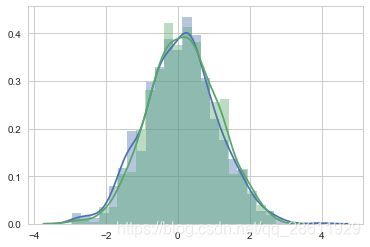
0.09815903489253375 大致相同,不能拒绝原假设。sns.distplot(X1_sample);
sns.distplot(X2_sample);