Manthan, Codefest 19 (open for everyone, rated, Div. 1 + Div. 2)F. Bits And Pieces

多亏了橘子猫的博客，让我明白了，橘子猫NB，这里贴一手他的博客链接
https://blog.csdn.net/ccsu_cat/article/details/100076916

题目链接：https://codeforces.com/contest/1208/problem/F

题意：给你 n 个数，求 $\max (a_i|(a_j\&a_k))$，i

思路：很容易想到枚举 i ,然后贪心，再然后就不知道该怎么写…

从后往前枚举 i ，然后对 $a_i$ 没有的高位有1加1，然后从这个1的集合一直贪下去。这样子就需要维护一个个集合，集合 $S(m)$ 代表满足 $a_j\in m$ 的数量，如果这个集合数量>=2，则 $a_i$ 肯定顺着 集合 S 走下去。

举个例子：
4
2 8 4 7

1. 当前为7 ，但是 i >=n-1 ,ai不能取;7的二进制为111，则S(7)=1; S(6)=1;S(5)=1;S(4)=1;S(3)=1;S(2)=1;S(1)=1;S(0)=1
2. 当前为4 ，但是 i >=n-1,ai不能取;4的二进制位100，则S(4) = 2
3. 当前为8，a2=8,其二进制位1000，前面还有更多高位，这里不予考虑了，，，倒数第四位自己为1，不需要跟着集合S走，拿走自己1，倒数第三位为0，集合S(1<<2) = 2,则这位拿走S的一个1，倒数第三位为0，需要参考S，由于之前拿走了一个，所以S((1<<2) +(1<<1)）= 1,拿不了。。。后面都拿不了了，则当前答案最大值为：8+4=12.
   4…

看了上面的过程，很容易一个ai 做的贡献就是给所有ai的子集+1，这就很容易想到枚举子集的操作了。

for(int i=S;i;i=(i-1)&S)
	dp[i]++;

但是由于题目数据太大，肯定会超时，所以必要要优化。很明显，题目数据 ai<=2e6,并且我们dp[i]只需要取值为0,1或者>=2就行了，所以状态数<=6e6，然而具体怎么实现呢。
举个例子, 设 $int$ $S,i$，并且 $i\&S=i,<==>i\in S（就是i是S的儿子）$，如果dp[i]>=2,但是我们当前在更新S，还需不需要继续往下更新 i 呢，仔细思考发现是没必要的。然后该怎么枚举呢。
很容易想到一个方法，枚举需要修改的低位1，画个图表示一下。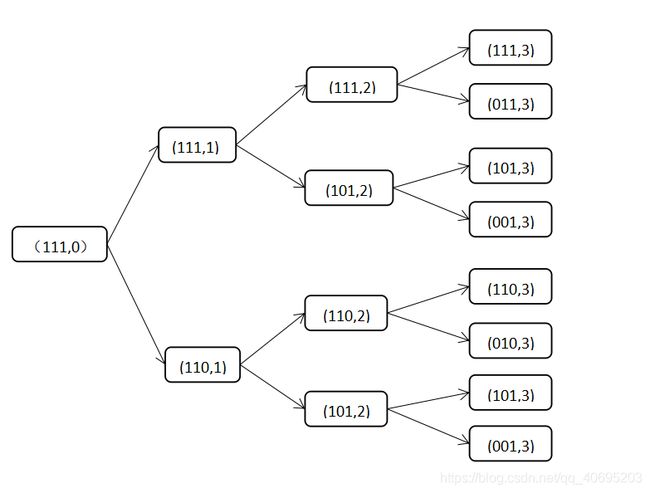

然后可以直接递归下去。
然后没啥好BB的，具体方式怎么写都行，就是防止一个点和他的儿子被一直加下去。

#include 
const int N=4e6+5;
const int M=21;
#define LL long long
using namespace std;
int a[N],n,dp[N];
void add(int x,int k,bool flag){
     
    if(k>=M||dp[x]>=2)return;
    add(x,k+1,1);
    if(!flag)dp[x]++;   //注意，这个flag是为了标记，每个x只会+一次
    if(x&(1<<k))
        add(x^(1<<k),k,0);
}
int main(){
     
    cin>>n;
    for(int i=1;i<=n;i++)
        scanf("%d",a+i);
    int ma=0;
    for(int i=n;i>=1;i--){
     
        int ans=0,x=0;
        for(int j=M-1;j>=0;j--)
            if(a[i]&(1<<j))
                ans=(ans<<1)+1;
            else if(dp[x|(1<<j)]>=2)
                ans=(ans<<1)+1,x|=(1<<j);
            else
                ans=(ans<<1);
        if(i<=n-2)
            ma=max(ma,ans);
        add(a[i],0,0);
    }
    cout<<ma;

   return 0;
}