题目链接:Codeforces Round #548 (Div. 2) D. Steps to One
题目大意:一个数列,一开始是空的,每次往他最后一个位置随机的加上一个[1,m]范围内的数字,然后对当前数列所有的数字求gcd,如果gcd不为1,那么就继续添加,否则停止。问最后这个数列期望的长度。
思路:拿到题目首先明白一定是道期望dp。我们考虑dp[x]为此时序列gcd为x,到序列gcd为1时(结束)的长度。由全期望公式![E[x]=\sum p[y]\cdot E[x\left | y].](http://img.e-com-net.com/image/info8/9a1154cd97e248c1b5cd103472c61efd.gif) 得
得
![dp[x]=1+\frac{\sum_{1}^{m}dp[gcd(x,i)]}{m}.](http://img.e-com-net.com/image/info8/092cb1360beb4151a0d0e9f30b594a58.gif)
由此我们得到了一个 的解法,显然复杂度时不够的 (1≤m≤100000).
的解法,显然复杂度时不够的 (1≤m≤100000).
因此我们考虑对每一个 来说
来说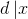 ,因此我们可以将枚举的复杂度降为
,因此我们可以将枚举的复杂度降为 ,令f(d)表示
,令f(d)表示![\sum_{1}^{m}\left [ gcd(x,i)==d \right ]](http://img.e-com-net.com/image/info8/7f92b754f92642d2a8b7b1773ace40b4.gif)
则上述状态转移可化为
![dp[x]=1+\frac{\sum dp[d]\cdot f(d) }{m}](http://img.e-com-net.com/image/info8/987dbdd37e7644deaa5bfb26d2352056.gif) ,其中
,其中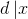
(可对f(d)反演,稍后再说)
现在来计算f(d):
对于集合
![\left \{ i \right|i\in \left [ 1,m\right ],gcd(x,i)=d}](http://img.e-com-net.com/image/info8/469e222fc64c4c2e83342051ce3dc77d.gif) ,令
,令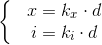 ,即
,即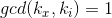 ,得到
,得到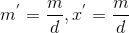 ,集合
,集合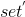 元素个数与原集合元素个数相同,该子问题转化为求在
元素个数与原集合元素个数相同,该子问题转化为求在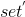 内有多少与x互质的元素。设n为
内有多少与x互质的元素。设n为 的质因子数量,则子问题复杂度为
的质因子数量,则子问题复杂度为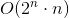 .
.
总时间复杂度为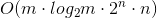
代码(注释有很多细节):
#include
#include
#include
#include
#include
#include
这道题的代码有很多值得学习的地方:
- 在线性筛的同时处理每个数的质因子。
- 因数分解的预处理。
- 取模的常数优化。
- 在计算f(n)的时候应用的容斥原理(原因是会有gcd(x,i)==x(

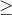
 ))),同时移项的时候也要注意!!!!!!(这一条其他题目也应用的非常多)
))),同时移项的时候也要注意!!!!!!(这一条其他题目也应用的非常多)
-
ll cnt=m/i;
dp[i]=rhs*m%mod*pow_mod(m-cnt,mod-2,mod)%mod;//移相结果
该部分代码为移项后的化简结果。
反演的方法日后再补。
![]() 得
得![]() 的解法,显然复杂度时不够的 (1≤m≤100000).
的解法,显然复杂度时不够的 (1≤m≤100000).![]() 来说
来说![]() ,因此我们可以将枚举的复杂度降为
,因此我们可以将枚举的复杂度降为![]() ,令f(d)表示
,令f(d)表示![\sum_{1}^{m}\left [ gcd(x,i)==d \right ]](http://img.e-com-net.com/image/info8/7f92b754f92642d2a8b7b1773ace40b4.gif)
![]()
![]() ,令
,令![]() ,即
,即![]() ,得到
,得到![]() ,集合
,集合![]() 元素个数与原集合元素个数相同,该子问题转化为求在
元素个数与原集合元素个数相同,该子问题转化为求在![]() 内有多少与x互质的元素。设n为
内有多少与x互质的元素。设n为![]() 的质因子数量,则子问题复杂度为
的质因子数量,则子问题复杂度为![]() .
.![]()

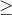
 ))),同时移项的时候也要注意!!!!!!(这一条其他题目也应用的非常多)
))),同时移项的时候也要注意!!!!!!(这一条其他题目也应用的非常多)