Codeforces 819 E. Mister B and Flight to the Moon

题意：

给定n 个点的完全图，用三元环和四元环去覆盖整张图。构造一个方案使得每条边被覆盖两次。

数据范围：

3 ≤ n ≤ 300

算法：

容易想到是要根据奇偶分别判断情况。

对于较为简单奇数：

• 将其中一个点拿出，在这里为了方便就暂时不考虑1号点。
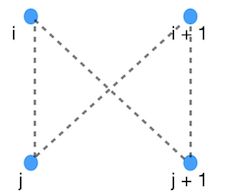
• 每两个点为一组，组与组之间没有重复点，如四个点为A,B,C,D A≠B≠C≠D
• 组与组之间连边是非常简单的，在下面提供了一种方案：
• 
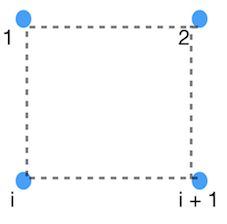
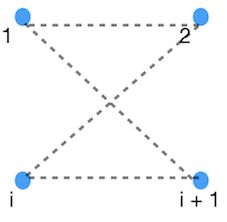
• 那么现在的问题就是组内点与点之间的连边，考虑刚才拿出的1号点：
• 。
• 将这些方案每个连两次，即满足题目要求。

对于偶数：

• 类比奇数的方法，拿出两个点，为了方便暂时不考虑1，2号点。
• 同样是分组，组与组之间的连边参照奇数的方案。
• 连完组之间的边后，没有覆盖的边只有1和2之间还有1，2点和各组内的边。
• 先考虑1和2之间的边覆盖（下图中i皆为3）：
  
  
  这样处理以后覆盖了1和2之间的连边还有1，2和第一组还有第一组内的边。
• 考虑最后剩下的组与1，2点之间的边，类似处理1和2点之间的边： (5 ≤ i ≤ 300)
  
  至此解决了题目中所有的情况。

代码：

#include 

using namespace std;

int main() {
    int n; scanf("%d", &n);
    printf("%d\n", (n & 1) ? (n - 1) + (n - 1) * ((n - 3) / 2) / 2: (n - 2) * (n - 2) / 4 + (n - 2));
    if (n & 1) {
        for (int i = 2; i <= n; i += 2) {
            printf("%d %d %d %d\n", 3, 1, i, i + 1);
            printf("%d %d %d %d\n", 3, 1, i, i + 1);
            for (int j = 2; j < i; j += 2) {
                printf("%d %d %d %d %d\n", 4, i, j, i + 1, j + 1);
                printf("%d %d %d %d %d\n", 4, i, j, i + 1, j + 1);
            }
        }
    }
    else {
        puts("4 1 2 3 4"), puts("4 1 3 4 2"), puts("4 1 4 2 3");
        for (int i = 5; i <= n; i += 2) {
            printf("%d %d %d %d \n", 3, 1, i, i + 1);
            printf("%d %d %d %d \n", 3, 2, i, i + 1);
            printf("%d %d %d %d %d\n", 4, 1, i, 2, i + 1);
            for (int j = 3; j < i; j += 2) {
                printf("%d %d %d %d %d\n", 4, i, j, i + 1, j + 1);
                printf("%d %d %d %d %d\n", 4, i, j, i + 1, j + 1);
            }
        }
    }
    return 0;
}