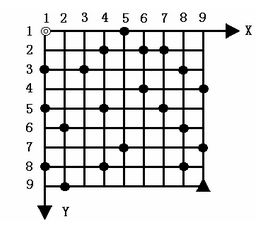
线性规划与网络流24题：《汽车加油行驶问题》

基于分层思想的最短路问题，将一维问题转化为多维空间中的问题解决！

分层思想很重要，一定要牢记啊！

它的优势就是在于把限制条件中的变量扩充，这样就解决了好多不确定的问题！可以建图的时候就方便多了！

算法思想：说到这个题目,应该说是刚开始的时候被他给吓到了，只是想着如何去把所有的条件构造起来，然后使用网络流的方式来解决问题！但是，如果真的是很冷静下来好好地思考这道题目，就会发现如果没有那些限制条件，就是一个求解最长路的题目，这样就可以直接使用ＳＰＦＡ来解决这个问题！关键就是在于这个每次最多只能走Ｋ个网格边，这样就是限制了活动的范围，使得有的边无法扩展！因此可以考虑使用这个分层思想的最短路问题！就是通过将每一个点进行拆分，这样，就是相当于一种分类讨论的方式！而分类讨论了之后，就知道哪些边是可以扩展的，哪些边是不能扩展的！关键点就是在于该如何选取变量来分层，这就是因情况而异了！像这道题目之中，就是通过油量的多少来扩展边的！分层思想，说穿了其实就是相当于这个动态规划之中的增加变量的方式来确定状态一样，他们的实质其实都是一样的！

本题之所以出现了比较多的问题：

总结下来，其实是有两点的啊！一点，就是这个距离刚开始在初始化的时候，没有看清楚ｓ的范围，导致初始化的时候出现了一些问题！还有，就是一点，那就是这个理解题意出错了！！把这个加油理解成了经过这个点的时候，可以加上，也可以不加，但是，其实，题目的意思是一定要加上的啊！这一点搞得我花了好长的时间调试啊！

感觉自己最近有进步了不少啊！

粘贴代码：

#include
#include
#include
#include
using namespace std;

#define maxN 110000
#define maxE 2000000
#define maxsize 1000000
#define INF 1<<30

struct Edge{
 int u,v,w,next;
};
Edge edge[maxE];
int cnt=0;
int q[maxsize];

bool mat[110][110];
int N,A,B,C,K;
int c[2]={0,0};
int s,t;

const int dx[]={-1,0,1,0};
const int dy[]={0,-1,0,1};

int index(int k,int x,int y){
 return k*N*N+N*x+y;
}

int head[maxN],d[maxN];
bool vis[maxN];

void addedge(int u,int v,int w){
 edge[cnt].u=u;
 edge[cnt].v=v;
 edge[cnt].w=w;
 edge[cnt].next=head[u];
 head[u]=cnt++;
}

void SPFA(){
 memset(vis,0,sizeof(vis));
 for(int i=0;i<=t;i++)
  d[i]=INF;
 d[s]=0;
 vis[s]=true;
 int l=0,r=0;
 q[r++]=s;
 while(l=1 && x<=N && y>=1 && y<=N){
       if(dir<=1){
        if(mat[x][y])    addedge(temp,index(K,x,y),B+A);
        else addedge(temp,index(k-1,x,y),B);
       }
       else{
        if(mat[x][y])   addedge(temp,index(K,x,y),A);
        else addedge(temp,index(k-1,x,y),0);
       }
      }
     }
     if(k!=K)   addedge(temp,index(K,i,j),A+c[mat[i][j]]);
    }
   }   
 SPFA();
 int ans=INF;
 for(k=0;k<=K;k++){ 
  if(d[index(k,N,N)]