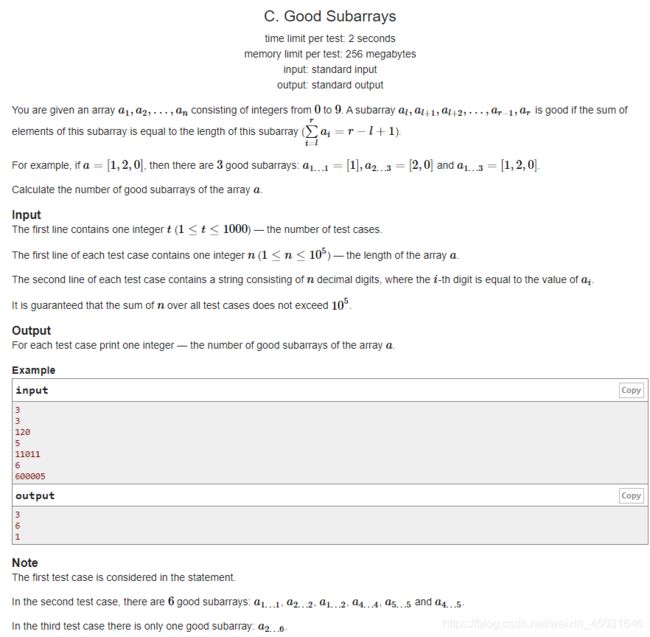
codeforces C. Good Subarrays

题目

题意：

在一个序列中，我们需要求出有多少个区间满足${\sum }_{i=l}^r{a}_i=r-l+1$。

思路：

在这题之前我们应该可以想到一个类似的一题，就是有多少个区间满足${\sum }_{i=l}^r{a}_i=0$，这个就是计算前缀和，如果某两个前缀和相等，那么也就是说明$cn{t}_{y+x}-cn{t}_x=0$满足${\sum }_{i=x}^{x+y}{a}_i=0$，所以这个区间就是一个满足条件的区间，所以就是求满足有多少个相等的前缀和。
本题的话就是求满足$$\begin{gathered} \sum _{i=x}^{x+y}{a}_i=x+y-x+1\to \sum _{i=x}^{x+y}{a}_i=\sum _{i=x}^{x+y}1 \\ \to \sum _{i=x}^{x+y}{a}_i-\sum _{i=x}^{x+y}1=0\to \sum _{i=x}^{x+y}{a}_i-1=0 \end{gathered}$$
这就和之前说的${\sum }_{i=x}^{x+y}{a}_i=0$的情况类似了。

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
typedef long long ll;
typedef vector<int> veci;
typedef vector<ll> vecl;
typedef pair<int, int> pii;
template <class T>
inline void read(T &ret) {
    char c;
    int sgn;
    if (c = getchar(), c == EOF) return ;
    while (c != '-' && (c < '0' || c > '9')) c = getchar();
    sgn = (c == '-') ? -1:1;
    ret = (c == '-') ? 0:(c - '0');
    while (c = getchar(), c >= '0' && c <= '9') ret = ret * 10 + (c - '0');
    ret *= sgn;
    return ;
}
inline void outi(int x) {if (x > 9) outi(x / 10);putchar(x % 10 + '0');}
inline void outl(ll x) {if (x > 9) outl(x / 10);putchar(x % 10 + '0');}
const int maxn = 1e5 + 10;
map<int, int> mp;
int main() {
    int t; read(t); while (t--) {
        mp.clear();
        int n; read(n);
        ll sum = 0, ans = 0;
        int x;
        mp[0]++;
        for (int i = 0; i < n; i++) scanf("%1d", &x), sum += x - 1, ans += mp[sum], mp[sum]++;
        printf("%lld\n", ans);
    }
    return 0;
}