codeforces D2. Prefix-Suffix Palindrome (Hard version)

题目

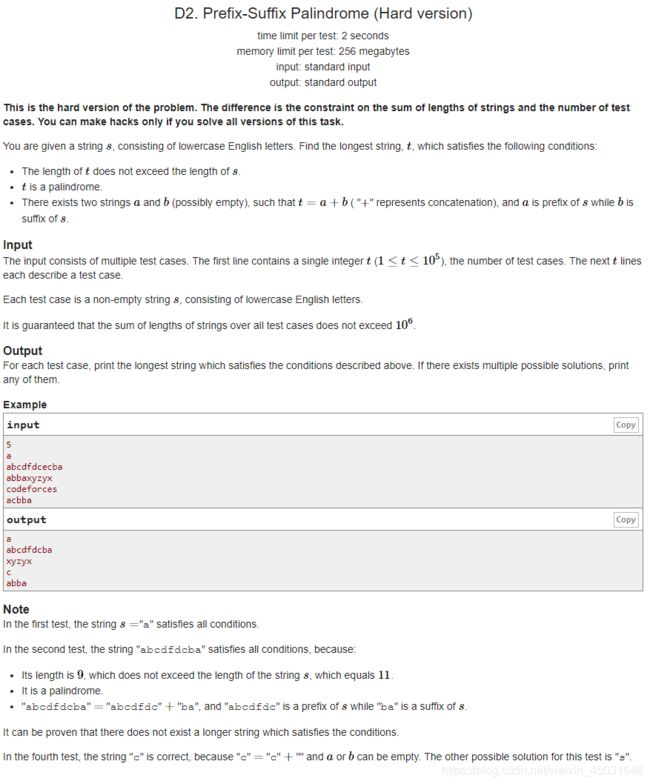
题意：

你有一个序列$s$，还有一个序列$t$，$t$的组成是有$s$的前缀和后缀组成的，但是要保证$t$最后是个回文串，前缀或者后缀可以为空字符串。

思路：

数据大了之后，主要的地方在于如何找到前缀和后缀中间的最长回文，一个回文也就是前缀=后缀，所以我们把前缀和后缀放到一起，变成一个新的字符串（中间要分隔开），然后也就是前缀要尽可能等于后缀，举个例子吧，假如从k开始的s要开始找到最长回文，那么新字符串是0开始的$S[0]....S[P]$是最长回文的话，那么新字符串中是不是有$S[S.size()-1-P].....S[S.size()-1]$也是最长回文，是不是突然发现了什么？没错，$KMP$算法（$kmp$这里就不说了），然后写一个模板就能过了。

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
typedef long long ll;
typedef vector<int> vec;
typedef pair<int, int> pii;
template <class T>
inline void read(T &ret) {
    char c;
    int sgn;
    if (c = getchar(), c == EOF) return ;
    while (c != '-' && (c < '0' || c > '9')) c = getchar();
    sgn = (c == '-') ? -1:1;
    ret = (c == '-') ? 0:(c - '0');
    while (c = getchar(), c >= '0' && c <= '9') ret = ret * 10 + (c - '0');
    ret *= sgn;
    return ;
}
inline void out(int x) {
    if (x > 9) out(x / 10);
    putchar(x % 10 + '0');
}
const int maxn = 1e6 + 10;
int nextn[maxn << 1];
string s, str;
int t, x;
string solve(string str) {
    s = str;
    reverse(s.begin(), s.end());
    s = str + '$' + s;
    nextn[0] = -1;
    int j = -1, i = 0;
    while (i < s.size()) {
        while (j != -1 && s[j] != s[i]) j = nextn[j];
        nextn[++i] = ++j;
    }
    return s.substr(0, j);
}
int main() {
    ios::sync_with_stdio(false);
    cin >> t;
    while (t--) {
        int k = 0;
        cin >> str;
        for (int i = 0; i < str.size(); i++) {
            if (str[i] == str[str.size() - i - 1]) k++;
            else break;
        }
        if (k + 1 > str.size()) {
            cout << str << endl;
            continue;
        }
        int cnt = 1;
        string ss = str.substr(k, str.size() - 2 * k);
        string x = solve(ss);
        reverse(ss.begin(), ss.end());
        string xx = solve(ss);
        for (int i = 0; i < k; i++) cout << str[i];
        if (xx.size() > x.size()) cout << xx;
        else cout << x;
        for (int i = k - 1; i >= 0; i--) cout << str[i];
        cout << endl;
    }
    return 0;
}