快速傅里叶变换FFT的C语言算法彻底研究
一、彻底理解傅里叶变换
快速傅里叶变换（Fast Fourier Transform)是离散傅里叶变换的一种快速算法，简称FFT，通过FFT可以将一个信号从时域变换到频域。
模拟信号经过A/D转换变为数字信号的过程称为采样。为保证采样后信号的频谱形状不失真，采样频率必须大于信号中最高频率成分的2倍，这称之为采样定理。
假设采样频率为fs，采样点数为N，那么FFT结果就是一个N点的复数，每一个点就对应着一个频率点，某一点n(n从1开始)表示的频率为：fn=(n-1)*fs/N。
举例说明：用1kHz的采样频率采样128点，则FFT结果的128个数据即对应的频率点分别是0，1k/128，2k/128，3k/128，…，127k/128 Hz。
这个频率点的幅值为：该点复数的模值除以N/2（n=1时是直流分量，其幅值是该点的模值除以N）。
二、傅里叶变换的C语言编程
1、对于快速傅里叶变换FFT，第一个要解决的问题就是码位倒序。
假设一个N点的输入序列，那么它的序号二进制数位数就是t=log2N.
码位倒序要解决两个问题：①将t位二进制数倒序；②将倒序后的两个存储单元进行交换。
如果输入序列的自然顺序号i用二进制数表示，例如若最大序号为15，即用4位就可表示n3n2n1n0，则其倒序后j对应的二进制数就是n0n1n2n3，那么怎样才能实现倒序呢？利用C语言的移位功能！
程序如下，我不多说，看不懂者智商一定在180以下！
复数类型定义及其运算
#define N 64 //64点
#define log2N 6 //log2N=6
/*复数类型*/
typedef struct
{
float real;
float img;
}complex;
complex xdata x[N]; //输入序列
/*复数加法*/
complex add(complex a,complex b)
{
complex c;
c.real=a.real+b.real;
c.img=a.img+b.img;
return c;
}
/*复数减法*/
complex sub(complex a,complex b)
{
complex c;
c.real=a.real-b.real;
c.img=a.img-b.img;
return c;
}
/*复数乘法*/
complex mul(complex a,complex b)
{
complex c;
c.real=a.real*b.real - a.img*b.img;
c.img=a.real*b.img + a.img*b.real;
return c;
}
/***码位倒序函数***/
void Reverse(void)
{
unsigned int i,j,k;
unsigned int t;
complex temp;//临时交换变量
for(i=0;i
{
k=i;//当前第i个序号
j=0;//存储倒序后的序号，先初始化为0
for(t=0;t
{
j<<=1;
j|=(k&1);//j左移一位然后加上k的最低位
k>>=1;//k右移一位，次低位变为最低位
}
if(j>i)//如果倒序后大于原序数，就将两个存储单元进行交换（判断j>i是为了防止重复交换）
{
temp=x[i];
x[i]=x[j];
x[j]=temp;
}
}
}
①第1级（第1列）每个蝶形的两节点“距离”为1，第2级每个蝶形的两节点“距离”为2，第3级每个蝶形的两节点“距离”为4，第4级每个蝶形的两节点“距离”为8。由此推得，
②对于16点的FFT，第1级有16组蝶形，每组有1个蝶形；第2级有4组蝶形，每组有2个蝶形；第3级有2组蝶形，每组有4个蝶形；第4级有1组蝶形，每组有8个蝶形。由此可推出，
③旋转因子
的确定
以16点FFT为例，第m级第k个旋转因子为
，其中k=0～2m-1-1，即第m级共有2m-1个旋转因子，根据旋转因子的可约性，
，所以第m级第k个旋转因子为
，其中k=0～2m-1-1。
为提高FFT的运算速度，我们可以事先建立一个旋转因子数组，然后通过查表法来实现。
complex code WN[N]=//旋转因子数组
{ //为节省CPU计算时间，旋转因子采用查表处理
//★根据实际FFT的点数N，该表数据需自行修改
//以下结果通过Excel自动生成
// WN[k].real=cos(2*PI/N*k);
// WN[k].img=-sin(2*PI/N*k);
{1.00000,0.00000},{0.99518,-0.09802},{0.98079,-0.19509},{0.95694,-0.29028},
{0.92388,-0.38268},{0.88192,-0.47140},{0.83147,-0.55557},{0.77301,-0.63439},
{0.70711,-0.70711},{0.63439,-0.77301},{0.55557,-0.83147},{0.47140,-0.88192},
{0.38268,-0.92388},{0.29028,-0.95694},{0.19509,-0.98079},{0.09802,-0.99518},
{0.00000,-1.00000},{-0.09802,-0.99518},{-0.19509,-0.98079},{-0.29028,-0.95694},
{-0.38268,-0.92388},{-0.47140,-0.88192},{-0.55557,-0.83147},{-0.63439,-0.77301},
{-0.70711,-0.70711},{-0.77301,-0.63439},{-0.83147,-0.55557},{-0.88192,-0.47140},
{-0.92388,-0.38268},{-0.95694,-0.29028},{-0.98079,-0.19509},{-0.99518,-0.09802},
{-1.00000,0.00000},{-0.99518,0.09802},{-0.98079,0.19509},{-0.95694,0.29028},
{-0.92388,0.38268},{-0.88192,0.47140},{-0.83147,0.55557},{-0.77301,0.63439},
{-0.70711,0.70711},{-0.63439,0.77301},{-0.55557,0.83147},{-0.47140,0.88192},
{-0.38268,0.92388},{-0.29028,0.95694},{-0.19509,0.98079},{-0.09802,0.99518},
{0.00000,1.00000},{0.09802,0.99518},{0.19509,0.98079},{0.29028,0.95694},
{0.38268,0.92388},{0.47140,0.88192},{0.55557,0.83147},{0.63439,0.77301},
{0.70711,0.70711},{0.77301,0.63439},{0.83147,0.55557},{0.88192,0.47140},
{0.92388,0.38268},{0.95694,0.29028},{0.98079,0.19509},{0.99518,0.09802}
};
3、算法实现
我们已经知道，N点FFT从左到右共有log2N级蝶形，每级有N/2L组，每组有L个。所以FFT的C语言编程只需用3层循环即可实现：最外层循环完成每一级的蝶形运算（整个FFT共log2N级），中间层循环完成每一组的蝶形运算（每一级有N/2L组），最内层循环完成单独1个蝶形运算（每一组有L个）。
/***【快速傅里叶变换】***/
void FFT(void)
{
unsigned int i,j,k,l;
complex top,bottom,xW;
Reverse(); //码位倒序
for(i=0;i
{ //一级蝶形运算
l=1<
for(j=0;j
{ //一组蝶形运算
for(k=0;k
{ //一个蝶形运算
xW=mul(x[j+k+l],WN[N/(2*l)*k]);//碟间距为l
top=add(x[j+k],xW);//每组的第k个蝶形
bottom=sub(x[j+k],xW);
x[j+k]=top;
x[j+k+l]=bottom;
}
}
}
}
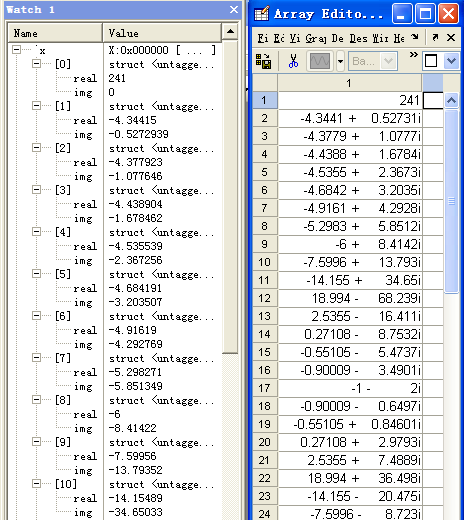
三、FFT计算结果验证
随便输入一个64点序列，例如
x[N]={{1,0},{3,0},{2,0},{5,0},{8,0},{4,0},{1,0},{3,0},{2,0},{5,0},{8,0},{4,0},{1,0},{3,0},{2,0},{5,0},{8,0},{4,0},{1,0},{3,0},{2,0},{5,0},{8,0},{4,0},{1,0},{3,0},{2,0},{5,0},{8,0},{4,0},{1,0},{3,0},{2,0},{5,0},{8,0},{4,0},{1,0},{3,0},{2,0},{5,0},{8,0},{4,0},{1,0},{3,0},{2,0},{5,0},{8,0},{4,0},{1,0},{3,0},{2,0},{5,0},{8,0},{4,0},{1,0},{3,0},{2,0},{5,0},{8,0},{4,0},{1,0},{3,0},{2,0},{5,0}};
在Keil中Debug查看数组变量x的FFT计算结果并与MATLAB计算结果进行比对，可以发现非常准确，说明程序编写正确！
