HDU 4576 Robot （概率 & 期望）

Robot

Time Limit: 8000/4000 MS (Java/Others)    Memory Limit: 102400/102400 K (Java/Others)
Total Submission(s): 779    Accepted Submission(s): 304

Problem Description

Michael has a telecontrol robot. One day he put the robot on a loop with n cells. The cells are numbered from 1 to n clockwise.



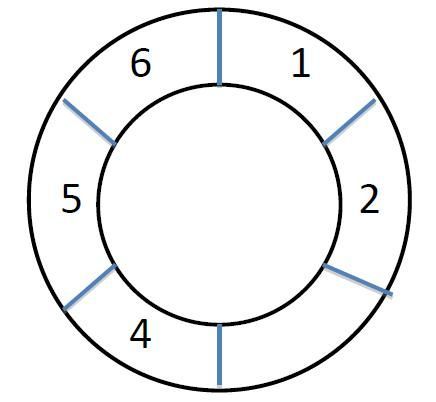
At first the robot is in cell 1. Then Michael uses a remote control to send m commands to the robot. A command will make the robot walk some distance. Unfortunately the direction part on the remote control is broken, so for every command the robot will chose a direction(clockwise or anticlockwise) randomly with equal possibility, and then walk w cells forward.
Michael wants to know the possibility of the robot stopping in the cell that cell number >= l and <= r after m commands.

 

 

Input

There are multiple test cases. 
Each test case contains several lines.
The first line contains four integers: above mentioned n(1≤n≤200) ,m(0≤m≤1,000,000),l,r(1≤l≤r≤n).
Then m lines follow, each representing a command. A command is a integer w(1≤w≤100) representing the cell length the robot will walk for this command.  
The input end with n=0,m=0,l=0,r=0. You should not process this test case.

 

 

Output

For each test case in the input, you should output a line with the expected possibility. Output should be round to 4 digits after decimal points.

 

 

Sample Input

3 1 1 2 1 5 2 4 4 1 2 0 0 0 0

 

 

Sample Output

0.5000 0.2500

 

 

Source

2013ACM-ICPC杭州赛区全国邀请赛

 

 题意：给你一个n，m，l，r。n个格子围成一个圈，一个机器人从第一个格子开始，经过m个步，每个步知道走几格，但是不知道方向，问你最后在l到r之间的概率。

#include<iostream>

#include<cstdio>

#include<cstring>



using namespace std;



const int N=220;



int n,m,l,r;

double dp[2][N];



int main(){



    //freopen("input.txt","r",stdin);



    while(~scanf("%d%d%d%d",&n,&m,&l,&r)){

        if(n==0 && m==0 && l==0 && r==0)

            break;

        for(int i=0;i<=n;i++)

            dp[0][i]=0;

        dp[0][0]=1;

        int x,cur=0;

        while(m--){

            scanf("%d",&x);

            for(int i=0;i<n;i++)

                dp[cur^1][i]=0;

            for(int i=0;i<n;i++){

                if(dp[cur][i]==0)

                    continue;

                dp[cur^1][((i-x)%n+n)%n]+=0.5*dp[cur][i];

                dp[cur^1][(i+x)%n]+=0.5*dp[cur][i];

            }

            cur^=1;

        }

        double ans=0;

        for(int i=l-1;i<r;i++)  //注意这里的范围

            ans+=dp[cur][i];

        printf("%.4lf\n",ans);

    }

    return 0;

}