Machine Learning入门笔记

machine learning的方式有两种

• 监督学习
• 无监督学习

事件问题分为两种：

• 回归问题
• 分类问题

线性回归代价函数

线性回归中代价函数为：
$$J=\frac{1}{2m}\sum _{i=1}^m(h_{(\theta )}(x^{(i)})-y^{(i)}{)}^2$$
说明：m为training set(训练集)内数据个数
疑问:为什么是除以2m，不应该除以m吗？
因为这里无论除以2m还是m，代价函数最优化的结果θ都是相同的。利用梯度下降法对JJ求导，如果是2m，求导结果为：
$$\frac{\partial j}{\partial {\theta }_i}=\frac{1}{m}\sum _{i=1}^m(h_{(\theta )}(x^{(i)})-y^{(i)})\frac{\partial h_{(\theta )}(x^{(i)})}{\partial \theta }$$
这里正好除以m，便于计算。

梯度下降算法

梯度下降算法：用于找到代价函数的最小值。
Batch梯度下降算法（梯度下降算法中的一种）：每一步下降都需要使用训练集全集。
也有其他梯度下降算法只需要使用到训练集子集的。

梯度下降算法的技巧：

特征缩放法：确保不同的特征都处于一个相近的范围内，这样梯度下降法就会更快地收敛。
举个例子
假如假设函数为$h(\theta )={\theta }_1{x}_1+{\theta }_2{x}_2$，$x_1$的取值范围是[1,2000]，而$x_2$的取值范围是[1，5]，这样子的代价函数如下图：
登高线都是很扁的椭圆，使用梯度下降的过程中会反复震荡，下降时间会十分漫长。

技巧一

将每一个特征值进行特征收缩，及每一个特征值都除以特征值的取值范围。$$x_1=\frac{size(0-2000)}{2000}$$$$x_2=\frac{numberofbedroom(1-5)}{5}$$确保$x_1$、$x_2$都在相近的取值范围中，这样子的代价函数图像图下：

变得比较圆了，使用梯度下降算法的速度也会十分快。

技巧二

在特征缩放中，也可以使用均值归一的方法
$$x_i=\frac{x_i-u_i}{s_i}$$其中$u_i$为平均值，$s_i$可以是标准差，
也可以是训练集中x的最大值减去最小值。
使用均值归一的方法可以使得特征值的平均值为0。

注意

确保特征值在相近的范围即可以了，不需要保持他们的范围是一样的。如下图：

学习率α

α取值过大，会导致代价函数J(θ)的值上下跳动或者越来越大。α取值过小，会导致梯度下降算法过慢。一般取α的值都是3倍递增地取。(…、0.001、0.03、0.1、0.3、1、3、10、…)

正规方程

正规方程：用于找到代价函数J(θ)的最小值。
$$\theta =(X^{T}X{)}^{-1}{X}^{T}y$$Octave:pinv$(X^{\prime }\ast X)\ast X^{\prime }\ast y$
此处的θ就是最优值

$(X^{T}X)$不可逆情况分析

说明，这种情况很少发生，就算$(X^{T}X)$不可逆，使用Octave的pinv函数依然能够正常运算
发生$(X^{T}X)$不可逆的情况有以下原因：

• 存在多余的特征
  （这种情况只要删除多余特征即可以）
• 特征个数大于训练集中数据个数
  （这种情况可以通过删除一些不重要的特征或者只用正则化的方法来解决）

梯度下降算法、正规方程比较

正规方程的优/缺点

优点

• 不需要选择α
• 不需要迭代

缺点

• 需要计算$(X^{T}X{)}^{-1}$，计算矩阵的逆的时间复杂度为O($n^3$)，当n(n为特征量的个数)十分大的时候，运算速度会十分的慢
• 不能用于那些更复杂的学习算法，但是能用于线性回归模型中

梯度下降算法的优/缺点

优点

• 能用在很多复杂的学习算法中
• n(n为特征量个数)很大的时候工作得很好

缺点

• 需要选择α(α为学习率)
• 需要多次迭代

怎么选择这两种算法

• 复杂的算法只能用梯度下降法
• 在线性回归模型中，n(特征量)为上百万的时候，使用梯度下降法；n为10000以内使用正规方程。

逻辑回归

逻辑回归是一种分类算法，用于2元分类两种情况，也可以使用‘一对余’的思想来实现多元分类

sigmoid function、logistic function

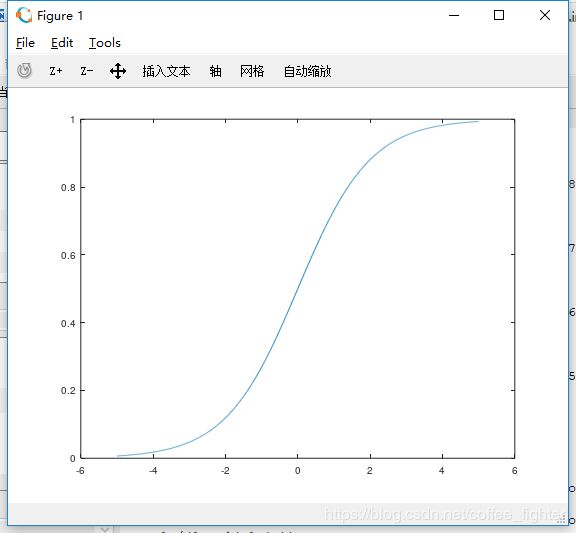
sigmoid function、logistic function都是同一种函数，如下：
$$y=\frac{1}{1+e^{-x}}$$
函数值范围在(0,1)，图像如下：

假设函数

$$h_{\theta }(x)=\frac{1}{1+e^{-F_{\theta }(x)}}$$
说明

• $h_{\theta }(x)$表示条件概率P(y=1|x;θ)（给定参数θ，具有x特征的条件下发生y=1的概率）
• $F_{\theta }(x)=0$为决策边界，决策边界就是区分y=0、1这两种情况的边界。
  如下图：
  
  $-1+x_1^2+x_2^2=1$为区分o和x的决策边界。该决策边界以外的是y=1的情况，以内是y=0的情况。
  注意，决策边界是假设函数及其参数的一个属性，不是训练集的属性。
  逻辑回归的单样本代价函数
  $$cost(h_{\theta }(x),y)=\{\begin{array}{l}-log(h_{\theta }(x)),y=1\\ -log(1-h_{\theta }(x)),y=0\end{array}$$
  可以合并成$cost(h_{\theta }(x),y)=-ylog(h_{\theta }(x))-(1-y)log(1-h_{\theta }(x))$
  整体代价函数
  $$J(\theta )=\frac{1}{m}cost(h_{\theta }(x),y)$$

过拟合

训练样本太少，无法约束过多的变量，导致过度拟合，对于训练集中的样本预测代价为0或者接近于0，这种模型泛化到新样本中（泛化：一个假设模型应用到新样本的能力）。

解决方法

1. 减少变量
2. 正则化

正则化

代价函数：
$$J(\theta )=\frac{1}{2m}[\sum _{i=1}^m(h_{(\theta )}(x^{(i)})-y^{(i)}{)}^2+\lambda \sum _{i=1}^m{\theta }_i^2]$$
其中，$\lambda {\sum }_{i=1}^m{\theta }_i^2$为正则化项，λ为拟合参数，过大的λ会导致所有θ都很小。
则这样子的代价函数就有两个作用：

1. ${\sum }_{i=1}^m(h_{(\theta )}(x^{(i)})-y^{(i)}{)}^2$可以使得参数拟合样本。
2. $\lambda {\sum }_{i=1}^m{\theta }_i^2$会尽可能地降低所有θ的值。

总的作用就是会使得相关性效地变量对应的θ值降低

逻辑回归的优化

优化有两种算法：

1. 梯度下降法
2. 正规方程法

正规方程法：
$$\theta =(x^{T}x+\lambda \left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& ...& :\\ 0& 0& ...& 1\end{array}\right]{)}^{-1}{x}^{T}y$$
说明：

• 因为加上了该矩阵，不存在矩阵不可逆这种情况（证明：阅读统计学相关知识，难，所以暂时略）
• 式子中的矩阵为n+1维方阵

梯度验证

梯度验证是一个用于验证代码是否有误的方法，一般用用于验证反向传播中的算法代码是否书写正确。
$$\frac{\partial J(\theta )}{\partial ({\theta }_1)}\approx \frac{J({\theta }_1+\epsilon ,{\theta }_2,...,{\theta }_n)-J({\theta }_1-\epsilon ,{\theta }_2,...,{\theta }_n)}{2\ast \epsilon }$$
$$\frac{\partial J(\theta )}{\partial ({\theta }_2)}\approx \frac{J({\theta }_1,{\theta }_2+\epsilon ,...,{\theta }_n)-J({\theta }_1,{\theta }_2-\epsilon ,...,{\theta }_n)}{2\ast \epsilon }$$
$$\frac{\partial J(\theta )}{\partial ({\theta }_n)}\approx \frac{J({\theta }_1,{\theta }_2,...,{\theta }_n+\epsilon )-J({\theta }_1,{\theta }_2,...,{\theta }_n-\epsilon )}{2\ast \epsilon }$$
其中ε一般取$10^{-4}$，如果上面的约等式子成立，说明代码没有错误。
注意，在真正训练神经网络模型的时候，记得要关闭梯度验证，因为梯度验证运行速度很慢。

神经网络算法θ随机初始化

在非神经网络算法中，如果权重的初始值都选为0，对结果没有影响，但是在圣经网络算法中，如果权重的初始值都选为0，则会造成特征的高度冗余。
所以初始化权重的时候，都调用
$${\theta }^n=rand(n,m)\ast 2\epsilon -\epsilon$$来确保每一个θ的初始化值在[-ε,ε)。

神经网络模型的选择

只有一个隐藏层的是最常用的，多个隐藏层的时候，每一层的单元个数最好都要相等。同时，每一层的单元个数越多越好，但是计算量会越来越大。

训练神经网络步骤：

1. 参数的随机初始化
2. 利用正向传播方法计算所有的ℎ()
3. 编写计算代价函数 的代码
4. 利用反向传播方法计算所有偏导数
5. 利用数值检验方法这些偏导
6. 使用优化算法来最小代价函数

算法诊断

发现训练的假设模型不理想的时候，通常是有两种原因造成的：

1. 高偏差（欠拟合）
2. 高方差（过拟合）

训练集、验证集（交叉验证集）、测试集

通常，会将全部样本随机分成训练集、验证集（交叉验证集）、测试集，它们的比例分别是3：1：1。
训练误差、验证误差、测试误差的计算公式都是：
$$J(\theta )=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x_i)-y_i)$$
这些集合的作用：

• 在多个预准备好的模型中，通过训练集拟合各个模型下的θ，通过验证集找出验证误差最小的一个模型，然后通过测试集来检验该模型的对新样本的泛化能力。
• 用训练集训练模型后，通过验证误差来查看该模型的好坏程度。
  举个例子:
  
  以上有10个预先准备好的模型，用训练集训练这10个模型，然后分别用验证集去计算这10个模型对应的验证误差，找去验证误差最小的模型，该模型就是10个模型中最适合的模型，并且可以通过测试误差来得出这个模型对新样本的泛化能力。

高偏差、高方差

高偏差：训练误差大、验证误差大
例子：用一个一次函数去拟合具有二次函数特性的样本
高方差：训练误差几乎为0，然而验证误差大
例子：用一个100次函数去拟合具有二次函数特性的样本

解决方案

高方差：

• 增加训练样本
• 减少特征
• 增大正则式子中的λ的值，加大对相关性不大的特征的惩罚力度

高偏差：

• 增加特性
• 增加多项式特征
• 减小正则式子中的λ的值。

偏斜类

什么是偏斜类？
假如在逻辑回归问题中，y=1占了99.5%，y=0占了0.5%，这种事件为偏斜类。

偏斜类遇到的问题

在偏斜类中，如果使用普通的验证误差来判断算法的好坏，容易被算法欺骗。因为在上面例子中，假设算法永恒输出都是y=1，则准确率已经到达了99.5%了，但是显然永恒输出y=1这个算法是很不合理的，这是我们就是被算法欺骗了。那在偏斜类的问题中，就不能使用验证误差来判断算法好坏。需要使用查准率、召回率来判断算法的好坏。

查准率、召回率

	实际值1	实际值0
预测值1	true positive	false positive
预测值0	false negative	true negative

查准率：$$P=\frac{truepostive}{truepostive+falsepostive}$$
召回率：$$R=\frac{truepostive}{truepostive+falsenegative}$$
查准率：预测正确中，实际为正确的比率
召回率：实际正确中，预测为正确的比率
$$F_1=\frac{2BP}{B+P}$$
那在偏斜类的问题中，就不能使用验证误差来判断算法好坏。需要使用F1判断算法的好坏，F1越高，说明该算法越好。同时，在逻辑回归问题中，使用F1来自动获取判定分界。（一般情况下，判断边界都为0.5）

SVM

（别问我为什么不继续更，因为我懒）