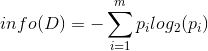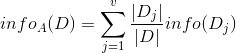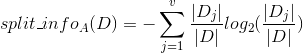决策树类的机器学习算法——决策树、Bagging、随机森林、Boosting、AdaBoost、GBDT、XGBoost
之所以将这几个算法记录在一起,是因为这些算法都是以决策树为基础!
1、决策树
决策树(decision tree)是一个树结构(可以是二叉树或非二叉树)。其每个非叶节点表示一个特征属性上的判定,每个分支代表这个特征属性在其值域上的输出,而每个叶节点存放一个类别。使用决策树进行决策的过程就是从根节点开始,测试待分类项中相应的特征属性,并按照其值选择输出分支,直到到达叶子节点,将叶子节点存放的类别作为决策结果。
决策树的构造过程不依赖领域知识,决策树的构造就是根据计算公式(信息增益比)来确定优先选择哪个特征属性对训练数据进行划分,依次类推,直到叶子节点(叶子节点中的数据都属于同一个类别)。究竟优先选择哪个特征属性?其评价标准是让各个分裂子集尽可能地“纯”,尽可能“纯”就是尽量让一个分裂子集中待分类项属于同一类别,而这个任务就交给数学公式——信息增益比——来确定!
分裂属性分为三种不同的情况:
1、属性是离散值且不要求生成二叉决策树。此时用属性的每一个划分作为一个分支。
2、属性是离散值且要求生成二叉决策树。此时使用属性划分的一个子集进行测试,按照“属于此子集”和“不属于此子集”分成两个分支。
3、属性是连续值。此时确定一个值作为分裂点split_point,按照>split_point和<=split_point生成两个分支。
属性选择度量算法有很多,一般使用自顶向下递归分治法,并采用不回溯的贪心策略。这里介绍ID3和C4.5两种常用算法。
1.1、ID3算法
先介绍几个概念,摘录自知乎:
熵:表示随机变量的不确定性。
条件熵:在一个条件下,随机变量的不确定性。
信息增益:熵 - 条件熵(在一个条件下,信息不确定性减少的程度!)
例如:
通俗地讲,X(明天下雨)是一个随机变量,X的熵可以算出来, Y(明天阴天)也是随机变量,在阴天情况下下雨的信息熵(即条件熵)我们如果也知道的话。两者相减就是信息增益!原来明天下雨例如信息熵是2,条件熵是0.01(因为如果是阴天就下雨的概率很大,信息就少了),这样相减后为1.99,在获得阴天这个信息后,下雨信息不确定性减少了1.99!是很多的!所以信息增益大!也就是说,阴天这个信息对下雨来说是很重要的!即这个特征属性很重要!所以在特征选择的时候常常用信息增益,如果IG(信息增益)大的话那么这个特征对于分类来说很关键~~ 决策树就是这样来找特征的!
从信息论知识中我们知道,期望信息越小(条件熵),信息增益(熵减去条件熵)越大,从而纯度越高。所以ID3算法的核心思想就是以——信息增益——度量属性选择,选择分裂后信息增益最大的属性进行分裂。下面先定义几个要用到的概念。
设D为用类别(公式中m为类别的总数)对训练元组进行的划分(划分为m个类),则D的熵(entropy)表示为:
其中pi表示第i个类别在整个训练元组中出现的概率,m表示类别的总数,可以用属于此类别元素的数量除以训练元组元素总数量作为估计。熵的实际意义表示是D中元组的类标号所需要的平均信息量。
现在我们假设将训练元组D按特征属性A进行划分,则A对D划分的期望信息为(即条件熵,在特征属性A分类的基础上):
Dj表示按特征属性A的一个分类,v表示特征属性A取值的种类个数。
信息增益即为两者的差值:
![]()
具体例子:
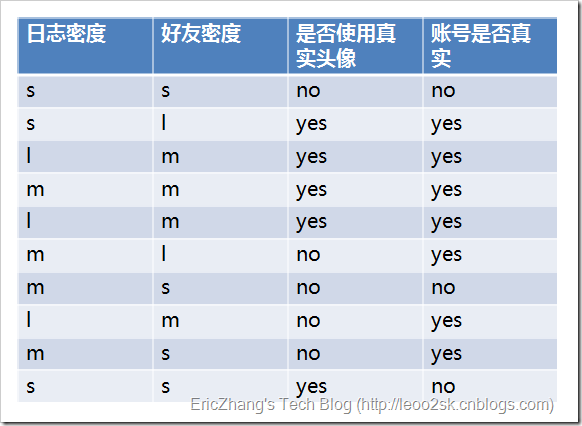
ID3算法就是在每次需要分裂时,计算每个属性的增益率,然后选择增益率最大的属性进行分裂。下面我们用SNS社区中不真实账号检测的例子说明如何使用ID3算法构造决策树。为了简单起见,我们假设训练集合包含10个元素:
其中s、m和l分别表示小、中和大。
设L、F、H和R表示日志密度、好友密度、是否使用真实头像和账号是否真实,下面计算各属性的信息增益。
![]()
![]()
因此日志密度的信息增益是0.276。
用同样方法得到H和F的信息增益分别为0.033和0.553。
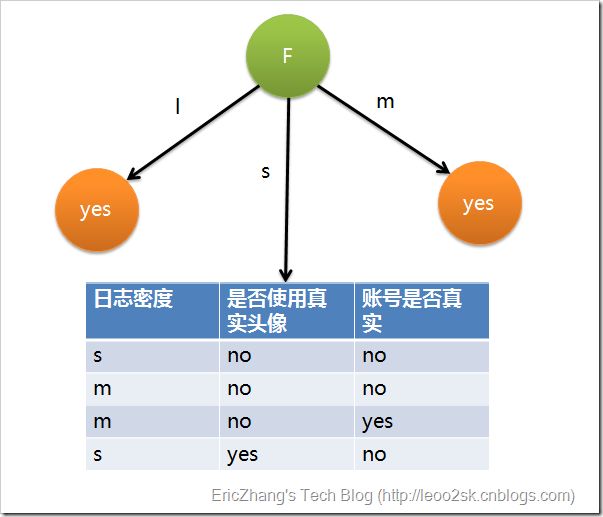
因为F具有最大的信息增益,所以第一次分裂选择F为分裂属性,分裂后的结果如下图表示:
在上图的基础上,再递归使用这个方法计算子节点的分裂属性,最终就可以得到整个决策树。
重要:
上面为了简便,将特征属性离散化了,其实日志密度和好友密度都是连续的属性。对于特征属性为连续值,可以如此使用ID3算法:先将D中元素按照特征属性排序,则每两个相邻元素的中间点可以看做潜在分裂点,从第一个潜在分裂点开始,分裂D并计算两个集合的期望信息,具有最小期望信息的点称为这个属性的最佳分裂点,其信息期望作为此属性的信息期望。
1.2、C4.5算法
ID3算法存在一个问题,就是偏向于多值属性,例如,如果存在唯一标识属性ID,则ID3会选择它作为分裂属性,这样虽然使得划分充分纯净,但这种划分对分类几乎毫无用处。ID3的后继算法C4.5使用增益率(gain ratio)的信息增益扩充,试图克服这个偏倚。
C4.5算法首先定义了“分裂信息”,其定义可以表示成:
其中各符号意义与ID3算法相同,然后,增益率被定义为:
C4.5选择具有最大增益率的属性作为分裂属性,其具体应用与ID3类似,不再赘述。
1.3、如果属性用完了怎么办
在决策树构造过程中可能会出现这种情况:所有属性都作为分裂属性用光了,但有的子集还不是纯净集,即集合内的元素不属于同一类别。在这种情况下,由于没有更多信息可以使用了,一般对这些子集进行“多数表决”,即使用此子集中出现次数最多的类别作为此节点类别,然后将此节点作为叶子节点。
1.4、关于剪枝
在实际构造决策树时,通常要进行剪枝,这时为了处理由于数据中的噪声和离群点导致的过分拟合问题。剪枝有两种:
先剪枝——在构造过程中,当某个节点满足剪枝条件,则直接停止此分支的构造。
后剪枝——先构造完成完整的决策树,再通过某些条件遍历树进行剪枝。
关于剪枝的具体算法这里不再详述,有兴趣的可以参考相关文献。
以上内容转载自: http://www.cnblogs.com/leoo2sk/archive/2010/09/19/decision-tree.html;略加补充,还需要继续加工,写的更加简明易懂。
2、Bagging
Bagging的策略:
(1)从样本集中重采样(有重复的)选出n个样本;
(2)在所有属性上,对这n个样本建立分类器(ID3、C4.5、CART、SVM、Logistic回归等);
(3)重复以上两步m次,即获得了m个分类器;
(4)将数据放在这m个分类器上,最后根据这m个分类器的投票结果,决定数据属于哪一类。
疑问1:n的值如何选择?
疑问2:m的值如何选择?——选择奇数个分类器即可。
注:与其将Bagging理解为一个算法,不如将其理解为一种思想,即综合多个弱分类器的结果得到一个强分类器的思想!
随机森林在bagging基础上做了修改。基本思路是:
(1)从样本集中用Bootstrap采样(有放回的采样)选出n个样本(重采样);
(2)从所有属性中随机选择k个属性,选择最佳分割属性作为节点建立CART决策树;
(3)重复以上两步m次,即建立了m棵CART决策树
(4)这m个CART形成随机森林,通过投票表决结果,决定数据属于哪一类
3.1、随机森林、Bagging和决策树的关系
目前的理解Bagging和随机森林的却别如红色字体标注所示;Bagging方法选用所有特征属性,随机森林选用所有特征属性中的k个特征属性(特征属性的一个子集)。
当然可以使用决策树作为基本分类器,但也可以使用SVM、Logistic回归等其它分类器,习惯上,这些分类器组成的“总分类器”,仍然叫做随机森林。以上参见自:http://blog.csdn.net/american199062/article/details/51314968
3.2、随机森林详述
决策树相当于一个大师,通过自己在数据集中学到的知识对于新的数据进行分类。但是俗话说得好,一个诸葛亮,玩不过三个臭皮匠。随机森林就是希望构建多个臭皮匠,希望最终的分类效果能够超过单个大师的一种算法。
那随机森林具体如何构建呢?有两个方面:数据的随机性选取,以及待选特征的随机选取。
3.2.1、数据的随机选取:
下图中,蓝色的方块代表所有可以被选择的特征,也就是目前的待选特征。黄色的方块是分裂特征。左边是一棵决策树的特征选取过程,通过在待选特征中选取最优的分裂特征(别忘了前文提到的ID3算法,C4.5算法,CART算法等等),完成分裂。右边是一个随机森林中的子树的特征选取过程。
4、Boosting
Boosting方法和Bagging类似,与其将其理解为一个算法,不如将其理解为一类算法的思想。即:通过m次的迭代,每次迭代训练出不同的弱分类器,然后将这m个弱分类器进行组合,形成一个强分类器。Adaboost就是这类算法中最具代表性的一个算法。
5、Adaboost
待补充
6、Boosting Tree
待补充
7、GBDT
待补充
8、XGBoost
待添加