Machine Learning 学习笔记Week3

本周主要涉及的内容是分类算法logistic regression algorithm。

有很多地方涉及到分类，例如判断一个邮件是否为垃圾邮件，判断一个肿瘤是否为恶性肿瘤。通常我们使用对于这种二值分类使用{0，1}来表示，不是0就是1，对于垃圾邮件是用0还是1代替是随意的。

logistic regression algorithm

那么我们如何根据以往的数据来判定一个新给定的数据的类别呢？如下图，假设0代表肿瘤为良性的，1代表肿瘤为恶性的。

（x1的点对应y的值为0.5）

假如我们按照线性回归的方式来求解的话，

则会得到以下hypothesis function:，最终不难得到一条直线。并且我们会最终得到以下结论：

（1）如果输入值下x>=x1,此时y>0.5,那么证明其输出值为1，为恶性肿瘤；

（2）如果输入值下x<x1,此时y<0.5,那么证明其输出值为0，为良性肿瘤。

这样看起来似乎没什么问题，一切都运行的很好，但是一旦训练集如下图分布：

可以看到对应y=0.5的横坐标的值由于某些点而右移了，但是显然大家应该想到对于那些y=1而x过大的点不应导致y=0.5时对应x的值的变化。

显然我们需要找到一种方法，使得

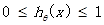
最后设计成这样的hypothesis function：

这个函数的图像如下图：

这个函数的名字叫做sigmoid function也称做logistic function。

因此此分类算法也就叫做logistic regression fucntion.

那么如何理解这个hypothesis function 的含义呢？

的值就是其预测对于某个输入x,其输出y=1的概率。

数学上的表达式就是：

Decision Boundary（决策边界）

决策边界的 概念很简单，顾名思义，就是能够将数据进行分类的函数。它是的固有属性，与数据集无关。

例如:

图中决策边界方程为

cost function

确定了hypothesis function之后，接下来就像linear regression中一样，如何确定hypothesis function中的参数值。

假如按照linear regression中一样，那样的话就是：

cost function：然后代入最后得到的是一个关于的函数。这个

是一个非凸函数(non-convex)。其图像如下：

从上图可以看出，有很多局部最优解，这样在运用梯度下降法时，很难收敛到全局最优解。

因此，我们侵向于找到这样一种cost function：

（1）对于某一输入x，

,并且正确的分类就是y=1，那么此时cost应该为0；反之若正确的为0，那么cost应该为无穷大；

（1）对于某一输入x，

,并且正确的分类就是y=0，那么此时cost应该为0；反之若正确的为1，那么cost应该为无穷大；

符合此条件的函数联想到了log函数。

最终设计的cost函数如下：

其中函数是将样本预测为1的概率大小。

把这个函数简写成一个数学表达式就是：

接下来就是运用梯度下降法来最小化costFunction.

方法如在线性回归中运用的一样：

想要最小化,

（同时更新所有的参数值）

求解其偏导数后得到：

Advanced Optimization

在上面计算的过程中我们需要计算:

这两项，

其实当我们计算完这两项后，我们完全有更好更高级的算法来优化，而不仅仅是使用梯度下降算法。

例如：共轭梯度算法，BFGS，L-BFGS等算法，这些算法相对于梯度下降算法有很好的优势，就是我们不需要人工选择学习速率,算法会自动选择，并且收敛速度很快；缺点便是这些算法使用和理解起来更复杂。

所以很多时候我们会用这些高级算法，但是这些高级算法的代码并不是自己写的，而是别人提供的第三方库。例如matlab 中提供的fminunc函数。

Multiclass Classfication

讲完{0，1}分类后，接下来便是多类别分类的情况，大致情况基本相似。我们只需要不停的重复二值分类的方法即可。

例如：下图是个3中类别的分类：

为了预测对于一个新的输入时属于{1，2，3}中的哪一类，我们需要先将2和3看成一类，1单独看成一类，如下图，求出hypothesis function；依次类推，取其中一类单独作为一类，剩余的类别作为一类，分别求出hypothesis function。然后对于这个新的输入分别代入这些hypothesis function中，求出其属于某一类别的概率；最后取这些概率的最大值，相应的类别就是我们预测的它属于的类别。

例如：对于新输入的x，我们有：,那我们就可以得出这个新的输入属于第一类的概率最大，它属于第一类。