基于MATLAB代码DWA算法的移动车路径规划

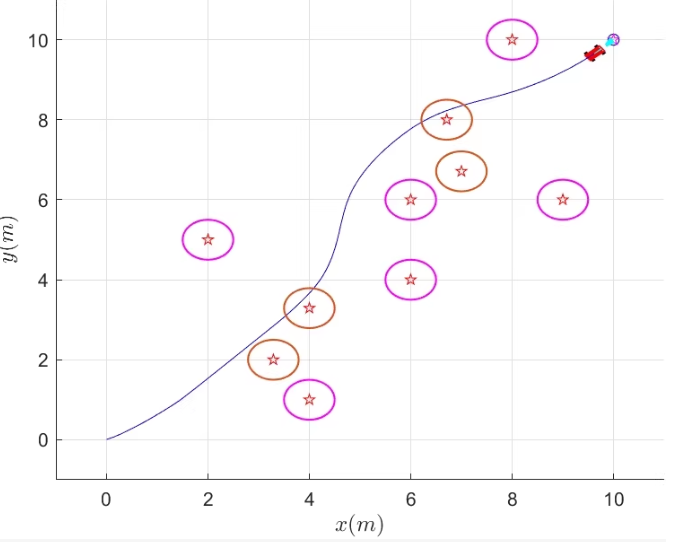
基于MATLAB代码DWA算法的移动车路径规划，可实现动态避障和静态避障

DWA（Dynamic Window Approach）是一种常用于移动机器人路径规划的局部路径规划算法。它通过在速度空间中采样，结合机器人的运动学约束和环境信息，选择最优的速度组合来实现避障和目标点导航。

以下是一个基于DWA算法的MATLAB代码示例，用于实现移动车的路径规划：

% DWA (Dynamic Window Approach) Algorithm for Mobile Robot Path Planning

clc;
clear;
close all;

%% 参数设置
dt = 0.1; % 时间步长
max_speed = 1.0; % 最大线速度 (m/s)
min_speed = -0.5; % 最小线速度 (m/s)
max_yaw_rate = pi / 4.0; % 最大角速度 (rad/s)
max_accel = 0.2; % 最大加速度 (m/s^2)
max_dyaw_rate = pi / 4.0; % 最大角加速度 (rad/s^2)
v_resolution = 0.01; % 线速度分辨率 (m/s)
yaw_rate_resolution = 0.1 * pi / 180.0; % 角速度分辨率 (rad/s)
predict_time = 3.0; % 预测时间范围 (s)
to_goal_cost_gain = 0.15; % 到达目标点代价权重
speed_cost_gain = 1.0; % 速度代价权重
obstacle_cost_gain = 1.0; % 障碍物代价权重
robot_radius = 0.2; % 机器人半径 (m)

%% 初始化
goal = [10, 10]; % 目标点位置 [x, y]
obstacles = [5, 5; 7, 7; 8, 8]; % 障碍物位置 [x, y]

pose = [0, 0, 0]; % 初始位置 [x, y, theta]
trajectory = pose;

%% 主循环
while true
    % 动态窗口计算
    [v_min, v_max, w_min, w_max] = calc_dynamic_window(pose, dt, max_speed, min_speed, ...
        max_yaw_rate, max_accel, max_dyaw_rate);
    
    % 轨迹评估
    [best_v, best_w, trajectory] = dwa_control(pose, [v_min, v_max, w_min, w_max], ...
        goal, obstacles, dt, predict_time, to_goal_cost_gain, speed_cost_gain, ...
        obstacle_cost_gain, robot_radius);
    
    % 更新机器人状态
    pose = motion(pose, best_v, best_w, dt);
    trajectory = [trajectory; pose];
    
    % 绘图
    clf;
    plot_trajectory(trajectory);
    hold on;
    plot_obstacles(obstacles, robot_radius);
    plot_robot(pose, robot_radius);
    plot_goal(goal);
    axis equal;
    grid on;
    xlim([-1, 11]);
    ylim([-1, 11]);
    drawnow;
    
    % 检查是否到达目标点
    if norm(pose(1:2) - goal) < 0.5
        disp('Goal reached!');
        break;
    end
end

%% 函数定义
function [v_min, v_max, w_min, w_max] = calc_dynamic_window(pose, dt, max_speed, min_speed, ...
        max_yaw_rate, max_accel, max_dyaw_rate)
    % 动态窗口计算
    v_min = max(min_speed, pose(3) - max_accel * dt);
    v_max = min(max_speed, pose(3) + max_accel * dt);
    w_min = max(-max_yaw_rate, pose(4) - max_dyaw_rate * dt);
    w_max = min(max_yaw_rate, pose(4) + max_dyaw_rate * dt);
end

function [best_v, best_w, trajectory] = dwa_control(pose, dw, goal, obstacles, dt, ...
        predict_time, to_goal_cost_gain, speed_cost_gain, obstacle_cost_gain, robot_radius)
    % DWA控制
    best_cost = inf;
    best_v = 0;
    best_w = 0;
    trajectory = [];
    
    for v = dw(1):v_resolution:dw(2)
        for w = dw(3):yaw_rate_resolution:dw(4)
            % 预测轨迹
            traj = predict_trajectory(pose, v, w, dt, predict_time);
            
            % 计算代价
            to_goal_cost = calc_to_goal_cost(traj, goal);
            speed_cost = calc_speed_cost(v, max_speed);
            ob_cost = calc_obstacle_cost(traj, obstacles, robot_radius);
            
            if isnan(ob_cost)
                continue;
            end
            
            final_cost = to_goal_cost_gain * to_goal_cost + ...
                         speed_cost_gain * speed_cost + ...
                         obstacle_cost_gain * ob_cost;
            
            % 更新最佳速度组合
            if final_cost < best_cost
                best_cost = final_cost;
                best_v = v;
                best_w = w;
                trajectory = traj;
            end
        end
    end
end

function traj = predict_trajectory(pose, v, w, dt, predict_time)
    % 预测轨迹
    traj = pose;
    time = 0;
    while time <= predict_time
        pose = motion(pose, v, w, dt);
        traj = [traj; pose];
        time = time + dt;
    end
end

function cost = calc_to_goal_cost(traj, goal)
    % 到达目标点代价
    dx = goal(1) - traj(end, 1);
    dy = goal(2) - traj(end, 2);
    cost = sqrt(dx^2 + dy^2);
end

function cost = calc_speed_cost(v, max_speed)
    % 速度代价
    cost = max_speed - abs(v);
end

function cost = calc_obstacle_cost(traj, obstacles, robot_radius)
    % 障碍物代价
    min_dist = inf;
    for i = 1:size(obstacles, 1)
        dx = obstacles(i, 1) - traj(:, 1);
        dy = obstacles(i, 2) - traj(:, 2);
        dist = sqrt(dx.^2 + dy.^2) - robot_radius;
        min_dist = min(min_dist, min(dist));
    end
    
    if min_dist < 0
        cost = NaN; % 发生碰撞
    else
        cost = 1.0 / min_dist; % 距离越小，代价越大
    end
end

function pose = motion(pose, v, w, dt)
    % 运动模型
    x = pose(1) + v * cos(pose(3)) * dt;
    y = pose(2) + v * sin(pose(3)) * dt;
    theta = pose(3) + w * dt;
    pose = [x, y, theta];
end

function plot_trajectory(trajectory)
    % 绘制轨迹
    plot(trajectory(:, 1), trajectory(:, 2), '-b');
end

function plot_obstacles(obstacles, robot_radius)
    % 绘制障碍物
    theta = linspace(0, 2*pi, 50);
    for i = 1:size(obstacles, 1)
        x = obstacles(i, 1) + robot_radius * cos(theta);
        y = obstacles(i, 2) + robot_radius * sin(theta);
        fill(x, y, 'r', 'FaceAlpha', 0.5);
    end
end

function plot_robot(pose, robot_radius)
    % 绘制机器人
    theta = linspace(0, 2*pi, 50);
    x = pose(1) + robot_radius * cos(theta);
    y = pose(2) + robot_radius * sin(theta);
    fill(x, y, 'g', 'FaceAlpha', 0.5);
end

function plot_goal(goal)
    % 绘制目标点
    plot(goal(1), goal(2), '*c', 'MarkerSize', 10, 'LineWidth', 2);
end
```![在这里插入图片描述](https://i-blog.csdnimg.cn/direct/b1cfecb071284fc28712a3557fb16557.png)


### 说明：
1. **参数设置**：可以根据实际需求调整参数，例如最大速度、加速度、预测时间等。
2. **动态窗口计算**：根据当前状态和约束条件计算可行的速度范围。
3. **轨迹评估**：通过采样速度组合，生成预测轨迹，并计算代价函数。
4. **运动模型**：使用简单的差分驱动模型更新机器人状态。
5. **可视化**：实时绘制机器人轨迹、障碍物和目标点。