经验小波变换(EWT)理论基础
项目说明
在信号分解领域,经验模态分解(EMD)十分经典,它基于信号特征自动地将信号分解为一组有限数目的 IMF 分量,在处理非线性和非平稳信号方面表现尤为出色,得到了广大学者的青睐。如今,EMD 方法在多个领域广泛应用,但是,在应用过程中会出现过包络、欠包络以及不同程度的端点效应和模态混叠问题,这给信号分解带来了许多问题。
EWT 是 Gilles 于 2013 年提出的非平稳信号处理方法,它融合了 EMD 方法的自适应分解理念和小波变换理论的紧支撑框架,为信号处理提供了一种全新的自适应时频分析思路。相比于 EMD 方法,EWT 方法能够自适应选择频带,克服了由于信号时频尺度不连续引发的模态混叠问题;同时,它具备完整可靠的数学理论基础,计算复杂度低,还能够克服 EMD 方法中过包络和欠包络的问题。因此,在信号处理尤其是故障诊断领域逐渐受到欢迎。
本章将主要介绍 EWT 方法的理论基础,并通过 EWT 和 EMD 分别实现仿真信号的信号分解进行对比,客观评价 EWT 方法的性能。
经验小波变换理论
EWT 方法的原理是将信号的 Fourier 谱划分成连续的区间,然后在每个区间上构造小波滤波器组进行滤波,最后通过信号重构得到一组调幅调频分量。该方法能够用具有紧支撑特性的小波滤波器组识别信号 Fourier 谱中特征信息所在的位置,自适应地提取到信号的不同频率成分。
EWT 频带划分方法
对于给定信号 f ( t ) f(t) f(t),首先对它进行傅里叶变换,经处理得到归一化在 2 π 2π 2π范围内的傅里叶频谱,根据香农准则,在分析过程中仅讨论 [ 0 , π ] [0, π] [0,π]上的信号特性。因此,将 Fourier频谱支撑区间定义在 [ 0 , π ] [0, π] [0,π]范围内。
假设该信号是由 N N N个单分量成分构成,那么在处理过程中 Fourier 谱的支撑区间被 ω n ω_n ωn分割成 N N N个连续的段(ωn 表示各段之间的边界),共有 N + 1 N+1 N+1个边界,其中 ω 0 = 0 ω0 =0 ω0=0, ω N = π ωN = π ωN=π。Fourier 轴的分割示意图参见下图。

Λ n Λ_n Λn表示划分结果,由下式表示
![]()
整个 Fourier 轴的支撑区间表示为:
 ω n ω_n ωn的确定思路为:对于信号 f ( t ) f(t) f(t)的傅里叶频谱,假设算法找到频谱中 M M M个极大值点,并对其降序排列,此时,Gilles 指出存在两种情况:
ω n ω_n ωn的确定思路为:对于信号 f ( t ) f(t) f(t)的傅里叶频谱,假设算法找到频谱中 M M M个极大值点,并对其降序排列,此时,Gilles 指出存在两种情况:
- M ≥ N M ≥ N M≥N时:表示选出极大值的数目足够多,可以为频谱分割提供依据。此时,保留前 N − 1 N-1 N−1个极大值;
- M < N M < N M<N时:表示信号中模式分量数目的预设值偏大。此时,将找到的 M M M个极大值保留,并重置参数 N N N,使 N = M N = M N=M。
这样,对于信号 f ( t ) f(t) f(t),设前 N N N个极大值在频域内对应的角频率 Ω n ( n = 1 , ⋯ , N ) \Omega_n(n=1, \cdots, N) Ωn(n=1,⋯,N),那么 EWT 的频带划分边界 ω n = Ω n + 1 + Ω n 2 \omega_n=\frac{\Omega_{n+1}+\Omega_n}{2} ωn=2Ωn+1+Ωn。为了方便后续过程中滤波器的构造,定义了宽度为 T n = 2 τ n T_n = 2τ_n Tn=2τn的过渡段(上图中的阴影区),这些过渡段都是以边界 ω n ω_n ωn为中心,其中 τ n = γ ω n ( 0 < γ < 1 ) τ_n=\gamma \omega_n (0<\gamma <1) τn=γωn(0<γ<1), γ < min n ( ω n + 1 − ω n ω n + 1 + ω n ) \gamma<\min_n(\frac{\omega_{n+1}-\omega_n}{\omega_{n+1}+\omega_n}) γ<minn(ωn+1+ωnωn+1−ωn)。
一般来说,对于没有先验信息可用的一段信号,猜测其模式的数目 N N N是比较困难的。为此,Gilles 提出了一种简单的 N N N值估计方法:检测信号的傅里叶谱中 M M M个极大值点,并将它们组成集合 { M i } k = 1 M \{M_i\}_{k=1}^M {Mi}k=1M,对集合中的 M i M_i Mi值按降序排列,得到 M 1 > M 2 > M 3 > ⋯ > M M M_1>M_2>M_3>\cdots>M_M M1>M2>M3>⋯>MM,设置阈值 M M + α ( M 1 − M M ) M_M+α(M_1-M_M) MM+α(M1−MM),此时大于阈值的极大值点的个数就是 N N N的值,其中 α α α为相对振幅比。这时,再按照上述的频谱分割方法即可得到信号的频带划分结果。
EWT 算法理论
经验小波是定义在区间 Λ n Λ_n Λn上的带通滤波器组,利用构建 Littlewood-Paley 和Meyer 小波的思想进行设计。对于 n > 0 n > 0 n>0,经验小波函数 ψ n ( ω ) \psi_n(\omega) ψn(ω)和经验尺度函数 φ n ( ω ) \varphi_n(\omega) φn(ω)分别由以下两式表示。

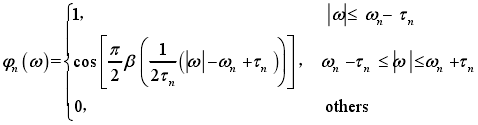
其中, β ( x ) = x 4 ( 35 − 84 x + 70 x 2 − 20 x 3 ) \beta(x)=x^4(35-84x+70x^2-20x^3) β(x)=x4(35−84x+70x2−20x3)。
根据上述滤波器的构造方法,只考虑 [ 0 , π ] [0, π] [0,π]的支撑区间,假定 Fourier 轴的分割边界 ω n = [ 0.598 , 1.024 , 2.370 , 2.768 ] ωn = [0.598, 1.024, 2.370, 2.768] ωn=[0.598,1.024,2.370,2.768],可建立下图所示的小波滤波器组。其中第一个区间为尺度函数确定的滤波器,其他区间为经验小波函数确定的带通滤波器,并以此为基础进行 EWT。

借鉴经典小波变换的思路,Gilles 构造的经验小波系数由内积产生,细节系数 W f e ( n , t ) W^e_f(n, t) Wfe(n,t)由经验小波函数 ψ n \psi_n ψn与信号 f ( t ) f(t) f(t)内积产生,可写成:
![]() 逼近系数 W f e ( 0 , t ) W^e_f(0, t) Wfe(0,t),由经验尺度函数 φ 1 \varphi_1 φ1与信号 f ( t ) f(t) f(t)内积产生,可写成:
逼近系数 W f e ( 0 , t ) W^e_f(0, t) Wfe(0,t),由经验尺度函数 φ 1 \varphi_1 φ1与信号 f ( t ) f(t) f(t)内积产生,可写成:
![]() 其中, ψ n ( ω ) \psi_n(\omega) ψn(ω)和 φ n ( ω ) \varphi_n(\omega) φn(ω)分别是 ψ n ( t ) \psi_n(t) ψn(t)和 φ n ( t ) \varphi_n(t) φn(t)的 Fourier 变换,傅里叶变换和逆变换分别记为 F [ ⋅ ] F[\cdot] F[⋅]和 F − 1 [ ⋅ ] F^{-1}[\cdot] F−1[⋅]。
其中, ψ n ( ω ) \psi_n(\omega) ψn(ω)和 φ n ( ω ) \varphi_n(\omega) φn(ω)分别是 ψ n ( t ) \psi_n(t) ψn(t)和 φ n ( t ) \varphi_n(t) φn(t)的 Fourier 变换,傅里叶变换和逆变换分别记为 F [ ⋅ ] F[\cdot] F[⋅]和 F − 1 [ ⋅ ] F^{-1}[\cdot] F−1[⋅]。
由此,信号 f ( t ) f(t) f(t)的重构表达式为:
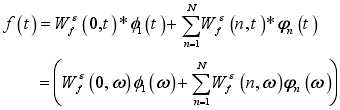 经 EWT 处理,信号 f ( t ) f(t) f(t)分解得到频率由低到高的调幅-调频单分量成分 f k ( t ) ( k = 1 , 2 , 3 … ) f_k(t) (k = 1, 2, 3…) fk(t)(k=1,2,3…):
经 EWT 处理,信号 f ( t ) f(t) f(t)分解得到频率由低到高的调幅-调频单分量成分 f k ( t ) ( k = 1 , 2 , 3 … ) f_k(t) (k = 1, 2, 3…) fk(t)(k=1,2,3…):
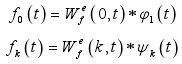
算法性能分析
通过上文中对 EWT 算法的介绍,我们知道,该方法可以根据信号 Fourier 谱的特点将复杂信号中频率不同的谐波进行有效分离,这种信号处理方法克服了模态混叠的影响,在一定程度上满足了对多分量信号分解的需求。
这里将用 EWT 方法分析谐波叠加信号和调幅调频信号,以验证 EWT 方法在信号分解方面的有效性。同时,与 EMD、EEMD 和 LMD 方法作对比,来说明 EWT方法的优越性。
本节构造一个谐波叠加信号 f s i g 1 ( t ) f_{sig1}(t) fsig1(t),使用 EWT 和 EMD 方法分别对其进行分解。仿真信号 f s i g 1 ( t ) f_{sig1}(t) fsig1(t)的表达式如下式所示。
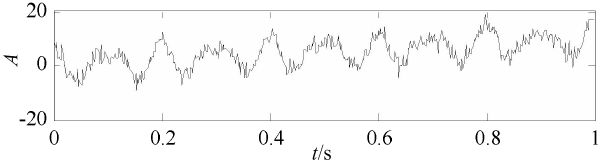
![]() 其中, n ( t ) n(t) n(t)为高斯白噪声,其标准差为 2.5 2.5 2.5。通过上式可知,仿真信号 f s i g 1 ( t ) f_{sig1}(t) fsig1(t)是由两个余弦信号组成,它们的频率分别是 10 H z 10 Hz 10Hz和 15 H z 15 Hz 15Hz。设定采样点数 N = 500 N = 500 N=500,采样频率 f s = 500 H z fs = 500 Hz fs=500Hz,采样时间 T = 1 s T = 1s T=1s,仿真信号 f s i g 1 ( t ) f_{sig1}(t) fsig1(t)的时域波形图如下图所示。
其中, n ( t ) n(t) n(t)为高斯白噪声,其标准差为 2.5 2.5 2.5。通过上式可知,仿真信号 f s i g 1 ( t ) f_{sig1}(t) fsig1(t)是由两个余弦信号组成,它们的频率分别是 10 H z 10 Hz 10Hz和 15 H z 15 Hz 15Hz。设定采样点数 N = 500 N = 500 N=500,采样频率 f s = 500 H z fs = 500 Hz fs=500Hz,采样时间 T = 1 s T = 1s T=1s,仿真信号 f s i g 1 ( t ) f_{sig1}(t) fsig1(t)的时域波形图如下图所示。
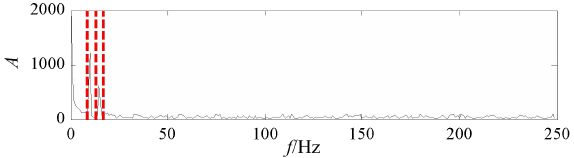
 采用 EWT 方法对该信号进行处理,根据分解理论,首先预设单分量个数 N = 4 N = 4 N=4,边界频率的确定方法为“locmaxmin”,即仿真信号的傅里叶频谱中两个频谱极大值之间的极小值点对应的频率,这样算法将 Fourier 谱划分为 4 4 4个频带,下图所示为EWT 方法的频带划分结果。
采用 EWT 方法对该信号进行处理,根据分解理论,首先预设单分量个数 N = 4 N = 4 N=4,边界频率的确定方法为“locmaxmin”,即仿真信号的傅里叶频谱中两个频谱极大值之间的极小值点对应的频率,这样算法将 Fourier 谱划分为 4 4 4个频带,下图所示为EWT 方法的频带划分结果。
 在上图划分的频带上建立小波滤波器组,通过滤波可以得到 4 组模式分量,由下图中C1~C4依次示出,前三个分量依次对应于仿真信号表达式中的 10t、5cos(20πt)和 2.5cos(30πt),每个模式分量的波形都清晰明显,可以清楚地分辨出每个模式的幅值和频率,高频的噪声分量也被完全分离到 C4 分量中,最大程度地保留了表达式中模式的单一性和完整性。
在上图划分的频带上建立小波滤波器组,通过滤波可以得到 4 组模式分量,由下图中C1~C4依次示出,前三个分量依次对应于仿真信号表达式中的 10t、5cos(20πt)和 2.5cos(30πt),每个模式分量的波形都清晰明显,可以清楚地分辨出每个模式的幅值和频率,高频的噪声分量也被完全分离到 C4 分量中,最大程度地保留了表达式中模式的单一性和完整性。

为了验证 EWT 方法在信号分解方面的优越性,采用 EMD 方法对上述信号 f s i g 1 ( t ) f_{sig1}(t) fsig1(t)进行分解。EMD 方法操作简单,处理速度快,同时,无需设置参数,在一定程度上避免了人为操作的盲目性。图 2-6 是信号 f s i g 1 ( t ) f_{sig1}(t) fsig1(t)的 EMD 分解结果。可以发现,该方法将 f s i g 1 ( t ) f_{sig1}(t) fsig1(t)分解成 7 个 IMF 分量,但由于 EMD 在迭代过程中每次都要找出信号中的极大值和极小值,导致 IMF4 和 IMF5 中都出现了频率为 15Hz 的谐波,即表达式中的 2.5cos(30πt),模态混叠现象严重。通过对比两种方法的结果,可以发现 EWT 方法能够抑制模态混叠现象,能够根据先验知识确定频带宽度,并将余弦信号完好地分解出来,抗噪声干扰能力强。
