算法总结归纳(第八天)(动态规划简单题、背包问题)
目录
一、动态规划五部曲
二、动态规划入门题
①、斐波那契数列
1、题目描述
2、解题思路
3、代码
②、爬楼梯
1、题目描述
2、解题思路
3、代码
③、最小花费爬楼梯
1、题目描述
2、解题思路
3、代码
④、不同路径Ⅰ
1、题目描述
2、解题思路
3、代码
⑤、不同路径Ⅱ
1、题目描述
2、解题思路
3、代码
⑥、整数拆分
1、题目描述
2、解题思路
3、代码
⑦、不同的二叉搜索树
1、题目描述
2、解题思路
3、代码
二、背包问题例题
1、01背包问题(二维背包)
1、题目描述
输入格式
输出格式
2、解题思路
3、代码
2、01背包问题(滚动数组)
Ⅰ、解题思路
Ⅱ、代码
3、完全背包问题
1、题目描述
输入格式
输出格式
2、解题思路
3、代码
4、多重背包问题Ⅰ
1、题目描述
输入格式
输出格式
2、解题思路
3、代码
5、多重背包问题Ⅱ
1、题目描述
输入格式
输出格式
2、解题思路
3、代码
6、分组背包问题
1、题目描述
输入格式
输出格式
2、解题思路
3、代码
一、动态规划五部曲
①、确定dp数组及下标含义
②、确定递推公式
③、dp数组初始化
④、数组遍历顺序
⑤、打印dp数组(可不进行)
下面题目均按照这个来分析
二、动态规划入门题
①、斐波那契数列
链接:斐波那契数列
1、题目描述
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
2、解题思路
本题目不需要动态规划也能做,
int fib(int n) {
if(n == 0) return 0;
if( n == 1) return 1;
return fib(n - 1) + fib(n - 2);
}但是我们要用简单题来锻炼动规的思维,接下来用动规的思路
①、确定dp数组含义
dp[i]我们就表示是i这个位置的大小
②、递推式
dp[i] = dp[i - 1] + dp[i - 2]。(i >= 2)。
③、初始化
dp[0] = 0,dp[1] = 1。其余位置初始化为0,
④、遍历
因为后面都是0,因此肯定是从前往后遍历。
3、代码
int fib(int n) {
int dp[31];
dp[0] = 0;dp[1] = 1;
for(int i = 2; i <= n; i++){
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}②、爬楼梯
题目链接:爬楼梯
1、题目描述
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
2、解题思路
①、确定dp数组含义
本题中每次可以爬1、2个楼梯,换句话说,就是到达该位置的方法,就是离该位置,只有1或者2差距的数组的和。dp[i] 表示到达i处用的方法有多少。
②、递推式
dp[i] = dp[i - 1] + dp[i - 2]。(i >= 2)。
③、初始化
那么dp[0]该是多少,dp[1] = 1. dp[2] = 2。因此dp[0]也应该初始化成1。
dp[0] = dp[1] = 1。其余位置均为0。
④、遍历
从前往后遍历。
3、代码
int climbStairs(int n) {
int dp[46];
dp[1] = dp[0] = 1;
for(int i = 2; i<=n; i++){
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}③、最小花费爬楼梯
题目链接:最小花费爬楼梯
1、题目描述
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
2、解题思路
①、确定dp数组含义
dp数组表示到达该楼层所用的最小花费。
②、递推式
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])。
③、初始化
dp[1] = dp[0] = 0。
④、遍历
从前往后遍历。
3、代码
int minCostClimbingStairs(vector& cost) {
int dp[1010];
dp[0] = 0;
dp[1] = 0;
for(int i = 2; i<=cost.size(); i++){
dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
}
return dp[cost.size()];
} ④、不同路径Ⅰ
题目链接:不同路径
1、题目描述
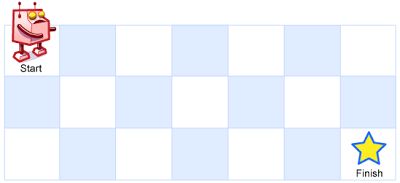
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
2、解题思路
①、确定dp数组含义
dp数组表示到达该点需要的步数是多少,
②、递推式
dp[ i ][ j ] = dp[i -1][ j ] + dp[ i ][ j - 1]。
因为机器人每次只能想下或向右走,换句话说,步数只能从左边或者上边推出来。
③、初始化
dp[1][1] = 1。这是因为,如果dp[1][1] == 0的话,根据递推公式所有数都是0了,这是不对的,我们设定初始为1,这样就能让每个步数递加了。
④、遍历
从上往下,从左往右,这是因为递推时候是从上面和左面推的,因此要优先初始化上面和左面。
3、代码
int uniquePaths(int m, int n) {
int dp[110][110];
for(int i = 1; i<=m; i++){
for(int j = 1; j<=n; j++){
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
dp[1][1] = 1;
}
}
return dp[m][n];
}⑤、不同路径Ⅱ
题目链接:不同路径Ⅱ
1、题目描述
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
2、解题思路
①、确定dp数组含义
dp数组依旧表示到达该位置用的步数。
②、递推式
dp[i][j] = dp[i - 1][ j ] + dp[ i ][ j - 1]
③、初始化
dp[1][1] = 1。如果遇到障碍物就将该位置dp值变为0.
④、遍历
从上到下,从左到右。
3、代码
int uniquePathsWithObstacles(vector>& obstacleGrid) {
if(obstacleGrid[0][0] == 1) return 0;//力扣测试用例在入口放了个障碍物,特判一下。
int dp[110][110];
int n = obstacleGrid.size();
int m = obstacleGrid[0].size();
for(int i = 1; i <= n; i++){
for(int j = 1; j<=m; j++){
if(obstacleGrid[i-1][j-1] == 1) dp[i][j] = 0;
else {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
dp[1][1] = 1;
}
}
}
return dp[n][m];
} ⑥、整数拆分
题目链接:整数拆分
1、题目描述
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
示例 1:
输入: n = 2 输出: 1 解释: 2 = 1 + 1, 1 × 1 = 1。
2、解题思路
①、确定dp数组含义
dp[i]表示下标为i的时候的乘积大小。
②、递推式
dp[i] = j * dp[i - j](其中i >= 3)。
③、初始化
dp[1] = 1.dp[2] = 2, dp[3] = 3。这是因为,这三个是最小的素数,这就意味着所有的更大的数的和都可以拆分成这几个数的和,进而转换为乘积。
④、遍历
两层循环,i表示当前数的乘积最大数,j从1开始遍历表示所有情况的最大值。
3、代码
int integerBreak(int n) {
if(n == 3) return 2;
if(n == 2) return 1;
int dp[60];
dp[1] = 1; dp[2] = 2;dp[3] = 3;
for(int i = 3; i<=n; i++){
for(int j = 1; j <= i; j++){
dp[i] = max(dp[i], j * dp[i - j]);
}
}
return dp[n];
}⑦、不同的二叉搜索树
题目链接:不同二叉搜素树
1、题目描述
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
输入:n = 3 输出:5
2、解题思路
①、确定dp数组含义
dp[i]表示i个数组成的二叉搜索树的个数。
②、递推式
dp[i] = dp[0] * dp[i] + dp[1] * dp[i - 1] + ……+ dp[i] * dp[0]。
③、初始化
dp[0] = 1,dp[1] = 1.dp[2] = 2。
④、遍历
遍历的话,最外层表示当前层数,内层的话则是从0到i进行遍历。然后所有情况相加。
3、代码
int numTrees(int n) {
int dp[21];
dp[0] = 1;dp[1] = 1; dp[2] = 2;
for(int i = 2; i < n; i++){
for(int j = 0; j<=i; j++){
dp[i + 1] += dp[j] * dp[i - j];
}
}
return dp[n];
}二、背包问题例题
1、01背包问题(二维背包)
题目链接:01背包问题
1、题目描述
有 N 件物品和一个容量是 V的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
2、解题思路
①、确定dp数组含义
我们用一个二维数组存储,每个dp[i][j]表示装到第i个物品,重量为j的时候背包的最大价值,
②、递推式
dp[ i ][ j ] = max(dp[ i-1 ][ j ], dp[ [i-1][j - w[i] ])。
③、初始化
dp[1][1] - dp[1][V] 均初始化成v[1]。其余初始化成0。
④、遍历
遍历从上到下,从左到右,因为,我们是从上方或者左方推导出来的。
先遍历物品,后遍历背包。
3、代码
#include
using namespace std;
#include
const int N = 1010;
int dp[N][N], w[N], v[N];
int main()
{
int n, V;cin>>n>>V;
for(int i = 1; i<=n; i++){
cin>>w[i]>>v[i];
}
for(int i = w[1]; i <= V; i++){
dp[1][i] = v[1];
}
for(int i = 2; i<=n; i++){
for(int j = 0; j <=V; j++){
if(j < w[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
}
}
cout< 2、01背包问题(滚动数组)
Ⅰ、解题思路
①、确定dp数组含义
dp[i] 表示容量为i的时候的最大价值,物品的状态被压缩了。
②、递推式
dp[j] = max(d[j], dp[ j - w [ i ]] + v[ i ])。
此处由二维数组推来。
③、初始化
依然是dp[ w[1] ] - dp[ V ]都被初始化成v[1]。
④、遍历
这个先遍历物品再遍历背包。同时需要注意,遍历背包是从后往前遍历,这是因为,我们数组要保存上一层的状态,因此从后往前可以防止因为前面的数组发生变化从而导致结果错误。
Ⅱ、代码
#include
using namespace std;
#include
const int N = 1010;
int dp[N], w[N], v[N];
int main()
{
int n, V;cin>>n>>V;
for(int i = 1; i<=n; i++){
cin>>w[i]>>v[i];
}
for(int i = w[1]; i<=V; i++){
dp[i] = v[1];
}
for(int i = 2; i <= n; i++){
for(int j = V; j >= w[i]; j--){
dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
}
}
cout< 3、完全背包问题
题目链接:完全背包问题
1、题目描述
有 N种物品和一个容量是 V 的背包,每种物品都有无限件可用。
第 i 种物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 种物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
2、解题思路
①、确定dp数组含义
dp[i] 表示容量为i的时候的最大价值。
②、递推式
dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
③、初始化
都为0就行。
④、遍历
本题和01背包几乎没有差别,就是背包的遍历顺序改为了从小到大。
3、代码
#include
using namespace std;
const int N = 1010;
int dp[N], w[N], v[N];
int main()
{
int n, V;
cin>>n>>V;
for(int i = 1; i <= n; i++){
cin>>w[i]>>v[i];
}
for(int i = 1; i <=n; i++){
for(int j =w[i]; j<=V; j++){
dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
}
}
cout< 4、多重背包问题Ⅰ
题目链接:多重背包问题
1、题目描述
有 N 种物品和一个容量是 V 的背包。
第 i 种物品最多有 si件,每件体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N 行,每行三个整数 vi,wi,si,用空格隔开,分别表示第 i 种物品的体积、价值和数量。
输出格式
输出一个整数,表示最大价值。
2、解题思路
本题把所有物品展开,其实就是物品有重复的01背包问题。按照01背包解题就行了。
①、确定dp数组含义
dp表示每个下标的最大值。
②、递推式
dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
③、初始化
都为0就行。
④、遍历顺序
与01背包相同。
3、代码
输入部分将所有数字均拆分成单个物品。
#include
using namespace std;
const int N = 11000;
int dp[N], w[N], v[N];
int main()
{
int n, V; cin>>n>>V;
int tem = 0;
while( n -- )
{
int a, b, p; cin>>a>>b>>p;
while(p -- )
{
tem ++;
w[tem] = a; v[tem] = b;
}
}
for(int i = 1; i<=tem; i++){
for(int j = V; j >= w[i]; j--){
dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
}
}
cout< 5、多重背包问题Ⅱ
题目链接:多重背包问题Ⅱ
1、题目描述
有 N 种物品和一个容量是 V 的背包。
第 i 种物品最多有 si件,每件体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N 行,每行三个整数 vi,wi,si,用空格隔开,分别表示第 i 种物品的体积、价值和数量。
输出格式
输出一个整数,表示最大价值。
2、解题思路
本题目是用二进制优化的思路。
例如7 = 1 + 1 + 1 + 1 + 1 + 1 + 1。这样拆7次,时间复杂度为O( n ),
但是如果我们用二进制的1、2、4、8来表示,
2可以用 1 + 1
3可以用 1 + 2.
4可以用 4
5 可以用 1 + 4
6 可以用 2 + 4
7可以用1 + 2 + 4。
时间复杂度变为了O(log n)。
①、确定dp数组含义
dp[i]表示下标的最大价值。
②、递推式
dp[j] = max(dp[j], dp[j - good.w] + good.v);
③、初始化
全为0就行
④、遍历
与01背包相同。
3、代码
#include
#include
#include
#include
using namespace std;
const int N = 2010;
int n, m;
int w[N], v[N], dp[N];
struct good
{
int w, v;
};
int main()
{
cin>>n>>m;
vector goods;
for(int i = 0; i>w>>v>>s;
for(int j = 1; j <= s; j*=2){
s -= j;
goods.push_back({w * j, v * j});
}
if(s > 0) goods.push_back({w * s, v * s});
}
for(auto good:goods)
for(int j = m; j >= good.w; j--)
dp[j] = max(dp[j], dp[j - good.w] + good.v);
cout< 6、分组背包问题
题目链接:分组背包问题
1、题目描述
有 N组物品和一个容量是 V 的背包。
每组物品有若干个,同一组内的物品最多只能选一个。
每件物品的体积是 vij,价值是 wij,其中 i 是组号,j 是组内编号。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行有两个整数 N,V,用空格隔开,分别表示物品组数和背包容量。
接下来有 N 组数据:
- 每组数据第一行有一个整数 Si,表示第 i 个物品组的物品数量;
- 每组数据接下来有 Si 行,每行有两个整数 vij,wij,用空格隔开,分别表示第 i 个物品组的第 j 个物品的体积和价值;
输出格式
输出一个整数,表示最大价值。
2、解题思路
①、确定dp数组含义
dp[i]表示下标的最大价值。
②、递推式
代码所示
③、初始化
全为0就行。
④、遍历
先遍历背包,再遍历每一组的最优解。本质还是01背包。
3、代码
#include
using namespace std;
const int N = 110;
int dp[N], w[N], v[N];
int main()
{
int n, m;
cin>>n>>m;
for(int i = 0; i>s;
for(int j = 0; j>w[j]>>v[j];
for(int j = m; j>=0; j--){
for(int k = 0; k= w[k])
dp[j] = max(dp[j], dp[j - w[k]] + v[k]);
}
}
}
cout<