树形dp模型整理

1072. 树的最长路径（活动 - AcWing）

思路：我们来看这里是求最长距离，很容易想到两次dfs，不是不可以，但是这题有负权边，那么实际就不能再这么写了，如下图：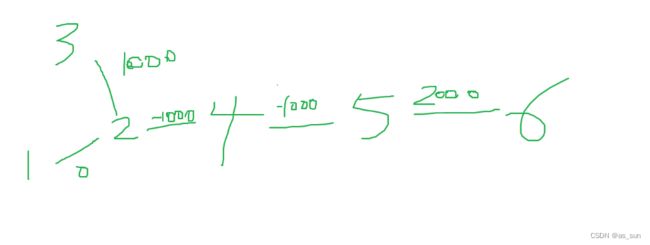

 很容易发现，如果从1开始找，最远的是3，然后3再找又是2，但是实际最长的再5-6那一段。所以就不能通过两次dfs来解决问题。这里我们引入树形dp来求解：

对于这样一棵树，我们将通过所有根(父)节点的距离划分它属于这个根节点(父)节点的一类。

那么我们如果能得到所有非叶子节点的距离，直接遍历就可以得到我们想要的结果了。

那么这个距离该怎么算呢？

显然我们可以记录子节点到父节点的最长距离和次长距离，通过两者的和得到。

这里还有一个重要条件，可以只有一个点，那么最小距离应该是0，所以我们最长距离和次长距离的记录初值赋成0即可，负值的话就不更新了。

#include
using namespace std;
int mx,idx;
const int N=10010,M=20010;
int h[N],ne[M],e[M],w[M],tmp;
void add(int a,int b,int c)
{
    e[tmp]=b,w[tmp]=c,ne[tmp]=h[a],h[a]=tmp++;
}
int st[N];
int dp[N];
int dfs(int u,int fa)
{
    int d1=0,d2=0;
    for(int i=h[u];i!=-1;i=ne[i])
    {
        int j=e[i];
        if(j==fa) continue;
        int t=dfs(j,u);
        t += w[i];
        //如果是负的话无所谓，反正这里不会被更新，那么就相当于下面不选就是，因为路径中可以只包含一个点，那么距离最小应该是1
        if(t>d1) d2=d1,d1=t;
        else if(t>d2) d2=t; 
    }
    dp[u]=max(dp[u],d1+d2);
    return d1;
}
int main()
{
    int n;
    scanf("%d",&n);
    memset(h,-1,sizeof h);
    tmp=0;
    for(int i=1;i

 1073. 树的中心（活动 - AcWing）

思路：这题的边权如果都是1的话，可以通过找最长路然后取一半得到，因为最长路上的点可以保证它到一边端点的距离一定是最远的，然后最长距离最小，那么就是取靠中间的位置，但是这道题显然这个做法就行不通了，因为这里有边权。 

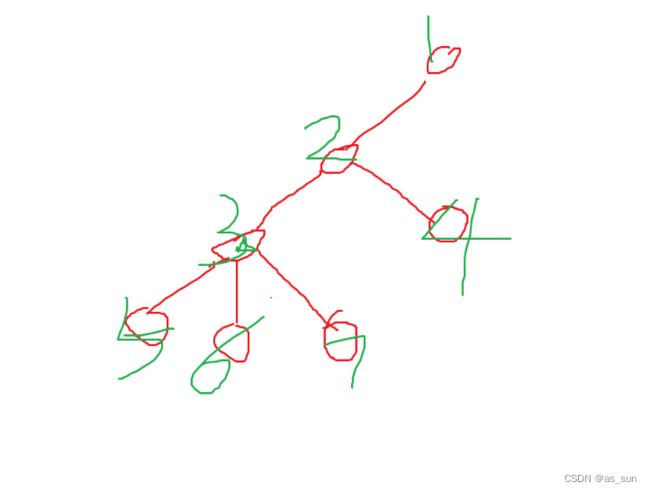
如图，如果我们要求3距离其他点的最远距离，那么它可以来自它的子节点(5，6，7)，也可以来自它的父节点2，如果来自父节点的话，也有两个取向，要么是来自父节点的父节点(1)，要么是来自兄弟节点。最远距离一定出现在这三种情况中的一种：

来自子节点很好说，我们记录子节点中距离最长的即可

如果来自父节点的另一子节点，那么就要考虑当前路径是否是最长的，如果是那么一定是往父节点的次长子节点那边延伸，如果当前的路径不是最长的，那么一定是往父节点的最长路径那边延伸。

如果来自父节点的父节点，那么我们先假设这个值可以被存在up[fa]中。

现在我们就要来考虑这些值如何计算：
首先最长和次长很好算，和上面一样，先往下递归，在回溯的时候进行记录，这里因为要被复用，那么我们记录在数组中即可。

然后很关键的就是up[fa]怎么算，显然是要用父节点去更新子节点，这个值显然是当前点到父节点的距离加上父节点的另一路径得到的，那么也是需要知道当前的路径是否是父节点的最长路径，那么一块儿记录就是。

这里我们既然指定了父子节点，那么相当于是有向的，遍历的时候记得要多传入一个参数。

另外，三个来源记得都要更新。

#include
using namespace std;
const int N=10010,M=20010;
int h[N],e[M],ne[M],w[M],idx;
void add(int a,int b,int c)
{
    e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
int d1[N],d2[N],zd1[N],zd2[N],up[N],dp[N];
int dfs1(int u,int fa)
{
    for(int i=h[u];i!=-1;i=ne[i])
    {
        int j=e[i];
        if(j==fa) continue;
        int t=dfs1(j,u)+w[i];
        if(t>d1[u]) d2[u]=d1[u],d1[u]=t,zd2[u]=zd1[u],zd1[u]=j;
        else if(t>d2[u]) d2[u]=t,zd2[u]=j;
    }
    return d1[u];
}
int dfs2(int u,int fa)
{
    for(int i=h[u];i!=-1;i=ne[i])
    {
        int j=e[i];
        if(j==fa) continue;
        //通过兄弟节点更新
        if(j==zd1[u]) up[j]=w[i]+d2[u];
        else up[j]=w[i]+d1[u];
        //通过父节点的父节点更新
        up[j]=max(up[j],up[u]+w[i]);
        dfs2(j,u);
    }
    dp[u]=max(d1[u],up[u]);
}
int main()
{
    int n;
    scanf("%d",&n);
    memset(h,-1,sizeof h);
    for(int i=1;i

1075. 数字转换（活动 - AcWing）

思路：这里除了那个步数外看似跟路径没有什么关系，但实际上，一个数和它的因数和可以相互妆转化，那么不就相当于建了无向边，然后多步数，不就相当于最远距离。这里最迷惑的地方在于，这个求因数和的过程，这里跟树没有关系，而且树应该不是连通的，最后构成的应该是森林，都不是在一棵树上，这更扰乱思维，所以核心不在于谁与谁能转化，在于最多多少步。

当然，我们也得求出谁和谁可以相互转化，很容易想到的思路就是试除法，但是显然时间复杂度是nsqrt(n)，不那么友好，这里我们逆向做，我们枚举每个数，去找它的倍数。也即：

for(int i=1;i<=n;i++)
{
    for(int j=i+i;j<=n;j+=i)
    {
        sum[j]+=i;
    }
}

 这样的时间复杂度就是O(nlogn)，显然比上面那个要好。

然后就是连边，要注意因数和一定是小于当前数，才能连边，另外由于跳转是在正整数范围内的，所以1与它的因数和0，不能连边：

    for(int i=2;i<=n;i++)//从2开，因为sum[1]=0,转换要在正整数范围内
    {
        if(sum[i]

ps:其实我们可以将sum[i]和i连边，然后从小到大去遍历即可。因为两个数相互跳转一定是因为有公因数，况且我们遍历的时候本来就有方向。只要我们能保证不影响遍历的顺序实际上连有向边是可以的。 

完整代码：

#include
using namespace std;
const int N=50010;
int sum[N];
int h[N],e[2*N],ne[2*N],idx;
void add(int a,int b)
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int dp[N];
int st[N];
int dfs(int u,int fa)
{
    st[u]=1;
    int d1=0,d2=0;
    for(int i=h[u];i!=-1;i=ne[i])
    {
        int j=e[i];
        if(j==fa) continue;
        int t=dfs(j,u)+1;
        if(t>d1) d2=d1,d1=t;
        else if(t>d2) d2=t;
    }
    dp[u]=max(dp[u],d1+d2);
    return d1;
}
int main()
{
    memset(h,-1,sizeof h);
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        for(int j=i+i;j<=n;j+=i)
        {
            sum[j]+=i;
        }
    }
    for(int i=2;i<=n;i++)//从2开，因为sum[1]=0,转换要在正整数范围内
    {
        if(sum[i]

1074. 二叉苹果树（活动 - AcWing）

思路：这里很显然，如果子节点要保留，那么父节点一定要保留。其实类似有依赖的背包问题，实际上也能用有依赖的背包问题来做这道题。但是这题每个点既然只有两条边，那么我们也不是非得把它复杂化。

如上图，我们定义dp[i][j]是以i为根节点，保留j条边的价值，属性是最大值。那么两个子节点就相当于两个物品组，从中进行选择，我们的决策可以按照给这个物品组分配多少条边来划分，然后递归方程就出来了。

dp[i][j]=dp[s][0](一个物品都不选)

dp[i][j]=dp[s][1]+w(只选一个)

... 

#include
using namespace std;
int n,m;
int dp[120][120];
int h[210],e[210],ne[210],w[210],idx;
void add(int a,int b,int c)
{
    w[idx]=c,e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int u,int fa)
{
    for(int i=h[u];i!=-1;i=ne[i])
    {
        if(e[i]==fa) continue;
        dfs(e[i],u);
        for(int j=m;j>=0;j--)
        {
            for(int k=0;k+1<=j;k++)//加的那个1，是因为子节点需要被放入，占用一个
            {
                dp[u][j]=max(dp[u][j],dp[u][j-k-1]+dp[e[i]][k]+w[i]);//这里相当于直接从只放子节点开始算的
            }
        }
    }
}
int main()
{
    memset(h,-1,sizeof h);
    scanf("%d%d",&n,&m);
    for(int i=1;i

323. 战略游戏（活动 - AcWing）

思路：可以观察到和自己相连的边，那么实际上也就是说一条边连接的两点至少选一个，和（285. 没有上司的舞会活动 - AcWing） 这题比较像，这题是同一条边连的两点最多选一个。

我们来分析这个题，如果一个节点被选，那么它的父节点和子节点可选可不选，如果如果一个节点没选，那么它的父节点或者子节点一定要被选，然后状态表示和状态转移差不多就出来了：

状态表示：定义以dp[u][1]表示以u为根的节点同时u被选的所有情况，dp[u][0]表示以u为根同时u没被选的情况。

状态计算：这样定义的话，那么显然我们就不用考虑从父节点转移而来的问题，因为我们定义的是以u为根的情况，那么只需要考虑从子节点转移的情况，而且最后的结果被累计在root节点上，城市构成一棵树，那么就只有一个根节点。

#include
using namespace std;
const int N=1600;
int h[N],e[N],ne[N],idx;
void add(int a,int b)
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int dp[N][N];
void dfs(int u)
{
    dp[u][0]=0,dp[u][1]=1;
    for(int i=h[u];i!=-1;i=ne[i])
    {
        int j=e[i];
        dfs(j);
        dp[u][0]+=dp[j][1];
        dp[u][1]+=min(dp[j][0],dp[j][1]);
    }
}
int st[N];
int main()
{
    int n;
    while(~scanf("%d",&n))
    {
        memset(h,-1,sizeof h);
        idx=0;
        memset(st,0,sizeof st);
        for(int i=1;i<=n;i++)
        {
            int x,c;
            scanf("%d:(%d)",&x,&c);
            for(int j=1;j<=c;j++)
            {
                int y;
                scanf("%d",&y);
                add(x,y);
                st[y]=1;
            }
        }
        int root;
        for(int i=0;i

 1077. 皇宫看守

思路：这题乍一看和上题有点相似，但是还是有不同的情况的，因为它不用每条边至少有一节点，如下图：

 

所以对于某一个点来说，它要么被自己的父节点看到，要么被自己的子节点看到。

对于每个点来说，它实际有三种状态，要么被它的父节点看到，要么被它的子节点看到，要么就是它自己放哨兵。我们可以定义三种状态：

0为被父节点看到：那么子节点放不放都可，因为它已经被看到了

1为被子节点看到：那么父节点放不放都可，因为它已经被看到了

2为自己放一个哨兵：那么父节点和子节点也是放不放都可

这里因为又有父节点，又有子节点不太方便，我们定义dp[u][s]为以u为根的三种情况：

dp[u][0]=min(dp[j][1],dp[j][2])+min(...)//j表示子节点，子节点的两种状态都可,每个子节点的情况都要累计到根节点去

dp[u][1]=dp[j][2]+min(dp[j1][1],dp[j1][2])+min(...)//有一个子节点必须放，剩下的子节点无所谓

dp[u][2]=min(dp[j][0],dp[j][1],dp[j][2])+min()//所有的子节点都是三种状态都可以

对于第二种情况我们枚举一下子节点即可

#include
using namespace std;
const int N=3000;
int h[N],e[N],ne[N],w[N],idx;
void add(int a,int b)
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int dp[N][4];
int st[N];
void dfs(int u)
{
    dp[u][0]=dp[u][1]=0,dp[u][2]=w[u];
    for(int i=h[u];i!=-1;i=ne[i])
    {
        int j=e[i];
        dfs(j);
        dp[u][0]+=min(dp[j][1],dp[j][2]);
        dp[u][2]+=min(dp[j][0],min(dp[j][1],dp[j][2])); 
    }
    dp[u][1]=1e9;
    for(int i=h[u];i!=-1;i=ne[i])
    {
        int j=e[i];
        dp[u][1]=min(dp[u][1],dp[u][0]-min(dp[j][1],dp[j][2])+dp[j][2]);
    }
}
int main()
{
    int n;
    scanf("%d",&n);
    memset(h,-1,sizeof h);
    for(int i=1;i<=n;i++)
    {
        int x,v,m;
        scanf("%d%d%d",&x,&v,&m);
        w[x]=v;
        for(int j=1;j<=m;j++)
        {
            int y;
            scanf("%d",&y);
            add(x,y);
            st[y]=1;
        }
    }
    int root;
    for(int i=1;i<=n;i++)
    {
        if(!st[i]) root=i;
    }
    dfs(root);
    cout<

ps:对于这种既要用父节点又要用子节点来更新的，我们就从状态机的角度来考虑，定义从根开始找，根据不同的情况用父节点来更新子节点。只有像上面那个树的中心那道题，因为每个点都由可能作为结果点，所以需要将每个点再用父节点更新一下，注意递归和更新的位置顺序即可。