强化学习原理python篇02——贝尔曼公式推导和求解

本章全篇参考赵世钰老师的教材 Mathmatical-Foundation-of-Reinforcement-Learning State Values and Bellman Equation章节，请各位结合阅读，本合集只专注于数学概念的代码实现。

概念

以bootstrapping来介绍状态值

bootstrapping（自举法）

让v代表从s1，…，s4的回报
$$\begin{gathered} v_1=r_1+{\gamma }_{r_2}+{\gamma }_{r_3}^2+...=r_1+\gamma v_2; \\ {v}_2=r_2+{\gamma }_{r_2}+{\gamma }_{r_3}^2+...=r_2+\gamma v_3; \\ {v}_3=r_3+{\gamma }_{r_2}+{\gamma }_{r_3}^2+...=r_3+\gamma v_4; \\ {v}_4=r_4+{\gamma }_{r_2}+{\gamma }_{r_3}^2+...=r_4+\gamma v_1; \end{gathered}$$
用矩阵表示为

[ v 1 v 2 v 3 v 4 ] = [ r 1 r 2 r 3 r 4 ] + γ [ 0 , 1 , 0 , 0 0 , 0 , 1 , 0 0 , 0 , 0 , 1 1 , 0 , 0 , 0 ] [ v 1 v 2 v 3 v 4 ] \left [\begin{matrix}v_1\\v_2\\v_3\\ v_4 \end{matrix} \right ] = \left [\begin{matrix}r_1\\r_2\\r_3\\ r_4 \end{matrix} \right ]+\gamma \left [\begin{matrix}0,1,0,0\\0,0,1,0\\0,0,0,1\\1,0,0,0 \end{matrix} \right ]\left [\begin{matrix}v_1\\v_2\\v_3\\ v_4 \end{matrix} \right ] ​v1​v2​v3​v4​​ ​= ​r1​r2​r3​r4​​ ​+γ ​0,1,0,00,0,1,00,0,0,11,0,0,0​ ​ ​v1​v2​v3​v4​​ ​
写作
$$\begin{gathered} v=r+\gamma Pv \\ v=(1-\gamma P{)}^{-1}r \end{gathered}$$

state value

$$S_t\stackrel{At}{\to }{S}_{t+1};R_{t+1}$$
表示从状态st做出动作at到$s_{t+1}$，并且获得鼓励$R_{t+1}$，从t开始，可以获得一个trajectory
$$S_t\stackrel{At}{\to }{S}_{t+1};R_{t+1}\stackrel{A_{t+1}}{\to }{S}_{t+2};R_{t+2}\stackrel{A_{t+2}}{\to }{S}_{t+3};R_{t+3}...$$

discounted return 为
$$\begin{gathered} G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+... \\ \gamma \in (0;1) \end{gathered}$$

state value 被定义为
$$v_{\pi }(s)=E[G_t|S_t=s]$$

贝尔曼公式（Bellman Equation）

首先，t 时候的trajectory的discount reward为
$$\begin{array}{rl}{G}_t=& R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...\\ =& R_{t+1}+\gamma (R_{t+2}+\gamma R_{t+3}+...)\\ =& R_{t+1}+\gamma G_{t+1}\end{array}$$

则该状态值为
$$\begin{array}{rl}{v}_{\pi }(s)=& E[G_t|S_t=s]\\ =& E[R_{t+1}+\gamma G_{t+1}|S_t=s]\\ =& E[R_{t+1}|S_t=s]+\gamma E[G_{t+1}|S_t=s]\end{array}$$
根据全期望公式（the law of total expectation）$E(E(Y|X))=E(Y)$

$$\begin{array}{rl}E[R_{t+1}|S_t=s]=& {\int }_{r\in R}r{f}_{R|S}(r|S_t=s)dr\\ =& {\int }_{r\in R}r\frac{f_{R,S}(r,S_t=s)}{f_S(S_t=s)}dr\\ =& {\int }_{r\in R}r\frac{f_{R,S}(r,S_t=s)}{f_{S,A}(S_t=s,A_t=a)}\cdot \frac{f_{S,A}(S_t=s,A_t=a)}{f_S(S_t=s)}dr\\ =& {\int }_{r\in R}r\frac{f_{R,S}(r,S_t=s)}{f_{S,A}(S_t=s,A_t=a)}\cdot f_{A|S}(a|S_t=s)dr\\ =& {\int }_{r\in R}r\frac{{\int }_{a\in A}{f}_{R,S,A}(r,a,S_t=s)}{f_{S,A}(S_t=s,A_t=a)}\cdot f_{A|S}(a|S_t=s)dr\\ =& {\int }_{r\in R}r{\int }_{a\in A}{f}_{R|S,A}(r|a,S_t=s)\cdot f_{A|S}(a|S_t=s)dadr\\ =& {\int }_{a\in A}{\int }_{r\in R}r{f}_{R_{t+1}|S,A}(r|a,S_t=s)\cdot \pi (a|s)dadr\\ =& {\int }_{a\in A}\pi (a|s)E(R_{t+1}|S=s,A=a)da\end{array}$$
同理
$$\begin{array}{rl}E[G_{t+1}|S_t=s]=& {\int }_{s^{\prime }\in S}p(s^{\prime }|s)E[G_{t+1}|S_t=s,S_{t+1}=s^{\prime }]d{s}^{\prime }\\ =& {\int }_{s^{\prime }\in S}p(s^{\prime }|s)E[G_{t+1}|S_{t+1}=s^{\prime }]d{s}^{\prime }(markovproperty)\\ =& {\int }_{s^{\prime }\in S}p(s^{\prime }|s)v_{\pi }(s^{\prime })d{s}^{\prime }\\ =& {\int }_{s^{\prime }\in S}{v}_{\pi }(s^{\prime }){\int }_{a\in A}p(s^{\prime }|s,a)p(a|s)dad{s}^{\prime }\\ =& {\int }_{s^{\prime }\in S}{v}_{\pi }(s^{\prime }){\int }_{a\in A}p(s^{\prime }|s,a)\pi (a|s)dad{s}^{\prime }\end{array}$$
因此，贝尔曼公式如下
$$\begin{array}{rl}{v}_{\pi }(s)=& E[R_{t+1}|S_t=s]+\gamma E[G_{t+1}|S_t=s]\\ =& {\int }_{a\in A}\pi (a|s)E(R_{t+1}|S=s,A=a)+\gamma {\int }_{s^{\prime }\in S}{v}_{\pi }(s^{\prime }){\int }_{a\in A}p(s^{\prime }|s,a)\pi (a|s)\\ =& {\int }_{a\in A}\pi (a|s){\int }_{r\in R}rf(r|s,a)drda+\gamma {\int }_{a\in A}f(s^{\prime }|s,a){\int }_{s^{\prime }\in S}{v}_{\pi }(s^{\prime })\pi (a|s)d{s}^{\prime }da\\ =& {\int }_{a\in A}{\int }_{r\in R}\pi (a|s)rf(r|s,a)drda+\gamma {\int }_{a\in A}{\int }_{s^{\prime }\in S}f(s^{\prime }|s,a)v_{\pi }(s^{\prime })\pi (a|s)d{s}^{\prime }da\\ =& {\int }_{a\in A}\pi (a|s)da[{\int }_{r\in R}rf(r|s,a)dr+\gamma {\int }_{s^{\prime }\in S}f(s^{\prime }|s,a)v_{\pi }(s^{\prime })d{s}^{\prime }]\\ =& {\int }_{a\in A}\pi (a|s)da[{\int }_{r\in R}{\int }_{s^{\prime }\in S}rf(r,s^{\prime }|s,a)dr+\gamma {\int }_{s^{\prime }\in S}{\int }_{r\in R}f(s^{\prime },r|s,a)v_{\pi }(s^{\prime })d{s}^{\prime }dr]\\ =& {\int }_{a\in A}\pi (a|s)da[{\int }_{r\in R}{\int }_{s^{\prime }\in S}rf(r,s^{\prime }|s,a)+\gamma f(s^{\prime },r|s,a)v_{\pi }(s^{\prime })d{s}^{\prime }dr]\\ =& {\int }_{a\in A}\pi (a|s)da[{\int }_{r\in R}{\int }_{s^{\prime }\in S}f(r,s^{\prime }|s,a)[r+\gamma \pi (s^{\prime })]d{s}^{\prime }dr]\end{array}$$

贝尔曼公式以及python实现

$$\begin{gathered} r_{\pi }(s)代表该状态得分的期望值 \\ {r}_{\pi }(s)={\int }_{a\in A}\pi (a|s){\int }_{r\in R}rf(r|s,a)drda \\ {p}_{\pi }(s^{\prime }|s)代表s转移到s‘的概率值 \\ {p}_{\pi }(s^{\prime }|s)={\int }_{a\in A}f(s^{\prime }|s,a)\pi (a|s) \end{gathered}$$
$$\begin{array}{rl}{v}_{\pi }(s)=& {\int }_{a\in A}\pi (a|s){\int }_{r\in R}rf(r|s,a)drda+\gamma {\int }_{a\in A}f(s^{\prime }|s,a){\int }_{s^{\prime }\in S}{v}_{\pi }(s^{\prime })\pi (a|s)d{s}^{\prime }da\\ =& r_{\pi }(s_i)+\gamma {\int }_{s^{\prime }\in S}{v}_{\pi }(s^{\prime })p_{\pi }(s^{\prime }|s)d{s}^{\prime }\end{array}$$
在离散状态下，该式子表现为
$$\begin{array}{rl}{v}_{\pi }(s)=& {\int }_{a\in A}\pi (a|s){\int }_{r\in R}rf(r|s,a)drda+\gamma {\int }_{a\in A}f(s^{\prime }|s,a){\int }_{s^{\prime }\in S}{v}_{\pi }(s^{\prime })\pi (a|s)d{s}^{\prime }da\\ v_{\pi }(s_i)=& r_{\pi }(s_i)+\gamma \sum _{s_j\in S}{v}_{\pi }(s_j)p_{\pi }(s_j|s_i)\end{array}$$
用矩阵形式表现为
$$\begin{gathered} v=r+\gamma Pv \\ v=(1-\gamma P{)}^{-1}r \end{gathered}$$

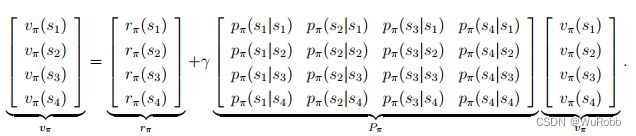
考虑以下情况

解法1——解析解

求解逆矩阵就可以获得该解

import numpy as np

## 贝尔曼公式状态值求解
def closed_form_solution(R,P,gamma):

    # 获取行号
    n = R.shape[0]
    # 生成单位阵
    I= np.identity(n)
    matrix_inverse = np.linalg.inv(I-gamma*P)

    # 矩阵点乘
    return matrix_inverse.dot(R)


R = np.array([(0.5*0+0.5*(-1)),1.,1.,1.]).reshape(-1,1)
P = np.array([
    [0,0.5,0.5,0],
    [0,0,0,1],
    [0,0,0,1],
    [0,0,0,1],
])

closed_form_solution(R,P,0.9)

输出：

array([[ 8.5],
       [10. ],
       [10. ],
       [10. ]])

解法2——迭代法

证明

def iterative_solution(n_iter, R, P, gamma):
    # n_iter 为迭代次数
    # 初始化  vπ
    n = R.shape[0]
    v = np.random.rand(n, 1)
    for iter in range(n_iter):
        v = R + (gamma * P).dot(v)
    return v


iterative_solution(100, R, P, 0.9)

输出：

array([[8.49974039],
       [9.99974039],
       [9.99974039],
       [9.99974039]])

atcion value

从a状态出发的行动所带来的回报的期望，数学符号表示为
$$q_{\pi }(s,a)=E[G_t|S_t=s,A_t=a]$$

action value 和 state value的联系，由全期望公式
$$\begin{array}{rl}{E}_{G_t}[G_t|S_t=s]=& E_{A_t|S_t}(E_{G_t}[G_t|(S_t=s,A_t|S_t=a)])\\ =& {\int }_{a\in A}{E}_{G_t}[G_t|S_t=s]\cdot \pi (a|s)da\end{array}$$
因此
$$\begin{array}{rl}{v}_{\pi }(s)=& {\int }_{a\in A}\pi (a|s)q_{\pi }(s,a)da\end{array}$$
代表的是state value是action value的期望

因此将贝尔曼公式代入，则
$$\begin{gathered} q_{\pi }(s,a)=r_{\pi }(s_i|a)+\gamma {\int }_{s_j\in S}{v}_{\pi }(s_j)p_{\pi }(s_j|s_i,a)ds \\ {v}_{\pi }(s)={\int }_{a\in A}\pi (a|s)[r_{\pi }(s_i|a)+\gamma {\int }_{s_j\in S}{v}_{\pi }(s_j)p_{\pi }(s_j|s_i,a)ds]da \end{gathered}$$

Ref

Mathematical Foundations of Reinforcement Learning，Shiyu Zhao