【图形学】直线光栅化算法(DDA算法,Bresenham算法和中点算法)
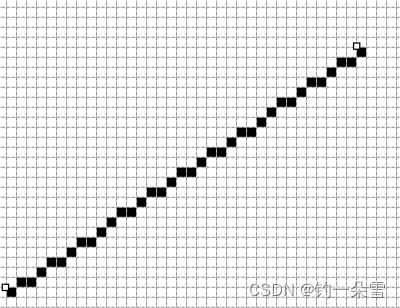
在数学上,直线就是由无穷多个点组成的, 在计算机屏幕显示的话, 需要做一些处理,对于光栅显示器,就是用有限多个点去逼近直线, 我们需要知道每一个像素点的坐标(都是整数)
数学上直线的方程如下 y = k x + b y=kx+b y=kx+b,给定直线的起点坐标 P 0 ( x 0 , y 0 ) P_0(x_0,y_0) P0(x0,y0)终点坐标 P 1 ( x 1 , y 1 ) P_1(x_1,y_1) P1(x1,y1)水平方向的位移 Δ x = x 1 − x 0 \Delta x=x_1-x_0 Δx=x1−x0垂直方向的位移 Δ y = y 1 − y 0 \Delta y=y_1-y_0 Δy=y1−y0 在直线的光栅化算法中要通过 Δ x 和 Δ y \Delta x 和 \Delta y Δx和Δy 的大小来确定绘图的主位移方向,主位移方向执行 ± 1 \pm1 ±1
| 条件 | 主方向 |
|---|---|
| Δ x > Δ y \Delta x>\Delta y Δx>Δy | x方向 |
| Δ x = Δ y \Delta x=\Delta y Δx=Δy | x方向或y方向 |
| Δ x < Δ y \Delta x<\Delta y Δx<Δy | y方向 |
DDA算法
直线的斜截式方程用微分的形式表示为 d y d x = Δ y Δ x = k \frac{dy}{dx}=\frac{\Delta y}{\Delta x}=k dxdy=ΔxΔy=k
那么可以得到直线上的像素点 P i + 1 和 P i P_{i+1}和P_{i} Pi+1和Pi的递推关系
{ x i + 1 = x i + Δ x y i + 1 = y i + Δ y = y i + k Δ x \begin{cases} x_{i+1}=x_i+\Delta x \\ y_{i+1}=y_i +\Delta y=y_i+k\Delta x \end{cases} {xi+1=xi+Δxyi+1=yi+Δy=yi+kΔx
以斜率 0 ≤ k < 1 0\leq k <1 0≤k<1为例,有 Δ x > Δ y \Delta x>\Delta y Δx>Δy ,主方向是x,那么上面的式子就变成了
{ x i + 1 = x i + 1 y i + 1 = y i + k \begin{cases} x_{i+1}=x_i+1 \\ y_{i+1}=y_i +k \end{cases} {xi+1=xi+1yi+1=yi+k
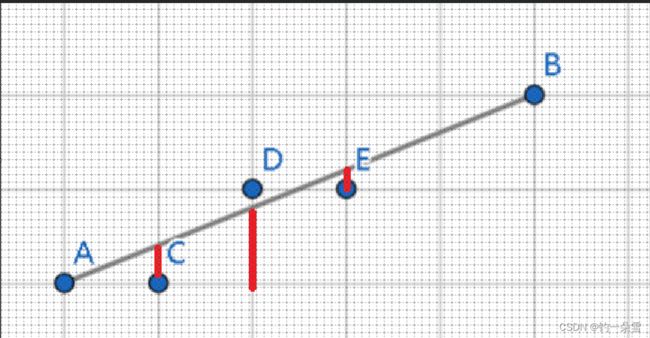
设点 E ( x i + 1 , y i + k ) E(x_i+1,y_i+k) E(xi+1,yi+k)是理想直线和线 x i + 1 = x i + 1 的交点 x_{i+1}=x_i+1的交点 xi+1=xi+1的交点那么用来逼近这个点的可能的像素点有两个 D ( x i + 1 , y i + 1 ) 和 C ( x i + 1 , y i ) D(x_i+1,yi+1)和C(x_i+1,y_i) D(xi+1,yi+1)和C(xi+1,yi)具体选择那个,就根据k的值确定(? y i + k y_i +k yi+k四舍五入? y i + 1 = i n t ( y_{i+1}=int( yi+1=int(y_i+k+0.5 ) ) ))

下面给出DDA算法画任意斜率直线的主要代码
void CLine::DrawLine(CDC* pDC)
{
int dx = m_p2.x - m_p1.x;//m_p1,m_p2(CPoint)
int dy = m_p2.y - m_p1.y;
double k = (double)(dy) / (double)(dx); //斜率
//确定主方向
int e = abs(k) > 1 ? abs(dy) : abs(dx);
double xadd = (double)(dx) / (double)(e);
double yadd = (double)(dy) / (double)(e);
double x = (double)(m_p1.x);
double y = (double)(m_p1.y);
for (int i = 0; i <= e; i++) {
pDC->SetPixel((int)(x + 0.5), (int)(y + 0.5), RGB(0, 0, 0));
x += xadd;
y += yadd;
}
}
Bresenham算法
Bresenham算法在主位移方向上也是移动一个单位,另一个方向移动0还是1取决于像素点和理想直线的距离d
还是以斜率 0 ≤ k < 1 0\le k <1 0≤k<1为例,x方向是主位移方向,点 Q ( x i + 1 , y i + 1 ) Q(x_{i+1},y_{i+1}) Q(xi+1,yi+1)是理想直线和 x i + 1 = x i + 1 x_{i+1}=x_i+1 xi+1=xi+1的交点,两个可能的像素的 P u p ( x i , y i + 1 ) 和 P d o w n ( x i , y i ) P_{up}(x_i,y_i+1) 和P_{down}(x_i,y_i) Pup(xi,yi+1)和Pdown(xi,yi),选那一个就取决于Q点和 P d o w n P_{down} Pdown的距离 d i + 1 d_{i+1} di+1,对于误差项d的计算向x方向递增1个单位就有 d i + 1 = d i + k d_{i+1}=d_i+k di+1=di+k,如果向y方向递增一个单位就还要减1。
d 0 = 0 y i + 1 = { y i + 1 , d i + 1 ≥ 0.5 y i , d i + 1 < 0.5 d_0=0 \\ \\ y_{i+1}=\begin{cases} y_{i}+1 ,d_{i+1}\geq 0.5\\ y_i,d_{i+1}<0.5 \end{cases} d0=0yi+1={yi+1,di+1≥0.5yi,di+1<0.5
不过通常不是用误差项d进行计算,取一个变量e, e 0 = − Δ x e_0=-\Delta x e0=−Δx,沿x方向每递增一个单位就有 e i + 1 = e i + 2 Δ y e_{i+1}=e_i+2\Delta y ei+1=ei+2Δy,当 e i + 1 ≥ 0 e_{i+1}\geq 0 ei+1≥0时下一个像素点就是( x i + 1 , y i + 1 x_i+1,y_i+1 xi+1,yi+1),并且要更新 e i + 1 = e i + 1 − 2 Δ x e_{i+1}=e_{i+1}-2\Delta x ei+1=ei+1−2Δx;否则下一个像素点就是( x i + 1 , y i x_i+1,y_i xi+1,yi)。
原始的Bresenham只能画指向第一象限并且斜率小于1的直线,但实际有这么多种情况,但是别慌,可以利用直线的对称性解决。

对于相同象限, 斜率不同的情况, 其实就是将斜率在0到1之间的线作关于函数y = x 对称而得到。对应到代码中就是将所有的y和所有的x调换位置。比如, e 0 = − Δ y e_0=-\Delta y e0=−Δy e i + 1 = e i + 2 Δ x e_{i+1}=e_i+2\Delta x ei+1=ei+2Δx,当 e i + 1 ≥ 0 e_{i+1}\geq 0 ei+1≥0时下一个像素点就是( x i + 1 , y i + 1 x_i+1,y_i+1 xi+1,yi+1),并且要更新 e i + 1 = e i + 1 − 2 Δ y e_{i+1}=e_{i+1}-2\Delta y ei+1=ei+1−2Δy;否则下一个像素点就是( x i + 1 , y i x_i+1,y_i xi+1,yi)。
下面给出通用的Bresenham算法
void CLine::DrawLine(CDC* pDC)
{
int dx = abs(m_p2.x - m_p1.x);//m_p1,m_p2(CPoint)
int dy = abs(m_p2.y - m_p1.y);
double k = (double)(dy) / (double)(dx); //斜率
BOOL wayChange = FALSE;//主方向是否发生改变,默认是x方向
int e,mainway,subway;
e = -dx;
mainway = dx;
subway = dy;
int addx, addy;
addx = (m_p2.x > m_p1.x) ? 1 : ((m_p2.x < m_p1.x) ? -1 : 0);
addy = (m_p2.y > m_p1.y) ? 1 : ((m_p2.y < m_p1.y) ? -1 : 0);
if (dy > dx) {//主方向是y
mainway = dy;
subway = dx;
wayChange = TRUE;
}
CPoint p = m_p1;
for (int i = 0; i <= mainway; i++) {
pDC->SetPixel(p, RGB(0, 255, 0));
if (wayChange)
p.y += addy;
else
p.x += addx;
e += 2 * subway;
if (e >= 0) {
if (wayChange)
p.x += addx;
else
p.y += addy;
e -= 2 * mainway;
}
}
}
中点算法
以第一象限斜率 0 ≤ k < 1 0\leq k<1 0≤k<1的直线为例。
直线的隐函数方程可以表示为 F ( x , y ) = y − k x − b = 0 F(x,y)=y-kx-b=0 F(x,y)=y−kx−b=0

A ( x i , y i ) , C ( x i + 1 , y i + 1 ) , D ( x i + 1 , y i ) , E ( x i + 1 , y i + 0 , 5 ) A(x_i,y_i),C(x_i+1,y_i+1),D(x_i+1,y_i),E(x_i+1,y_i+0,5) A(xi,yi),C(xi+1,yi+1),D(xi+1,yi),E(xi+1,yi+0,5)
将点E带入直线的隐函数方程有 d i = F ( x i + 1 , y i + 0.5 ) = y i + 0.5 − k ( x i + 1 ) − b d_i=F(x_i+1,y_i+0.5)=\\y_i+0.5-k(x_i+1)-b di=F(xi+1,yi+0.5)=yi+0.5−k(xi+1)−b
同判断 d i d_i di的正负就可以知道点E在直线的下方还是上方,从而确定选择点C还是选择点D
y i + 1 = { y i + 1 d i < 0 y i d i ≥ 0 \begin{equation} y_{i+1}=\left\{ \begin{aligned} y_i+1\quad d_i<0\\ y_i\quad d_i \geq0 \end{aligned} \right . \end{equation} yi+1={yi+1di<0yidi≥0
接下来就是求中点误差项d的递推公式
d 0 = 0.5 − k 当 d i < 0 时选择了点 C ( x i + 1 , y i + 1 ) 下一步要进行判断的中点就是 M ( x i + 2 , y i + 1.5 ) , 带入直线方程就是 d i + 1 = d i + 1 − k 当 d i > = 0 时选择了点 D ( x i + 1 , y i ) , 下一步要进行判断的中点就是 M ( x i + 2 , y i + 0.5 ) 带到直线方程就是 d i + 1 = d i − k d_0=0.5-k\\当d_i<0时选择了点C(x_i+1,y_i+1)下一步要进行判断的中点就是M(x_i+2,y_i+1.5),带入直线方程就是d_{i+1}=d_i+1-k 当d_i>=0时选择了点D(x_i+1,y_i),下一步要进行判断的中点就是M(x_i+2,y_i+0.5)带到直线方程就是d_{i+1}=d_i-k d0=0.5−k当di<0时选择了点C(xi+1,yi+1)下一步要进行判断的中点就是M(xi+2,yi+1.5),带入直线方程就是di+1=di+1−k当di>=0时选择了点D(xi+1,yi),下一步要进行判断的中点就是M(xi+2,yi+0.5)带到直线方程就是di+1=di−k
求出来了中点误差项,但这并不是我们想要的,因为这个递推是中有小数(0.5,k),我们需要的是进行整数运算。
这里引入新的值e
e 0 = Δ x − 2 Δ y 当 e i < 0 时 e i + 1 = e i + 2 Δ x − 2 Δ y 当 e i ≥ 0 时 e i + 1 = e i − 2 Δ y e_0= \Delta x-2\Delta y\\当e_i<0时e_{i+1}=e_i+2\Delta x-2\Delta y\\当e_i\geq0时e_{i+1}=e_i-2\Delta y e0=Δx−2Δy当ei<0时ei+1=ei+2Δx−2Δy当ei≥0时ei+1=ei−2Δy
下面是通用的中点算法
void CLine::DrawLine(CDC* pDC)
{
int dx = abs(m_p2.x - m_p1.x);//m_p1,m_p2(CPoint)
int dy = abs(m_p2.y - m_p1.y);
BOOL wayChange = FALSE;//主方向是否发生改
int e, mainway, subway;
mainway = dx;
subway = dy;
int addx, addy;
addx = (m_p2.x > m_p1.x) ? 1 : ((m_p2.x < m_p1.x) ? -1 : 0);
addy = (m_p2.y > m_p1.y) ? 1 : ((m_p2.y < m_p1.y) ? -1 : 0);
if (dy > dx) {//主方向是y
mainway = dy;
subway = dx;
wayChange = TRUE;
}
e =mainway-2*subway;
CPoint p = m_p1;
for (int i = 0; i < mainway; i++) {
pDC->SetPixel(p, RGB(0, 255, 0));
if (wayChange)
p.y += addy;
else
p.x += addx;
e -= 2 * subway;
if (e < 0) {
if (wayChange)
p.x += addx;
else
p.y += addy;
e += (2 * mainway - 2 * subway);
}
}
}