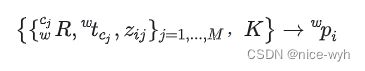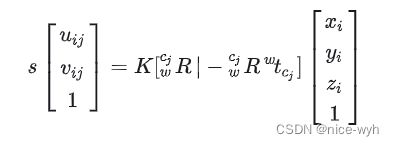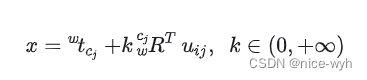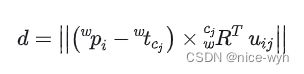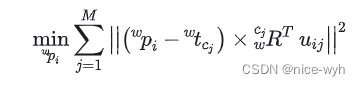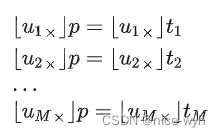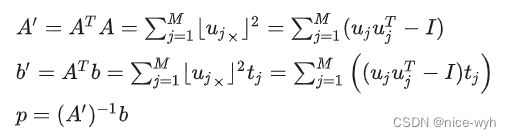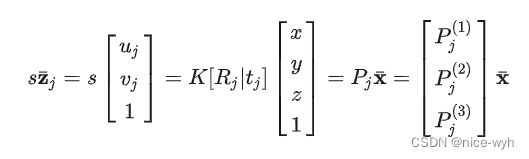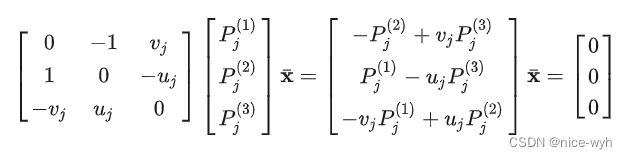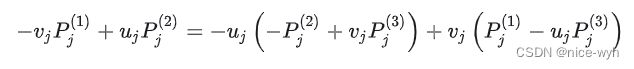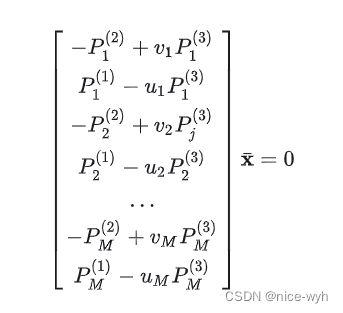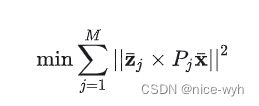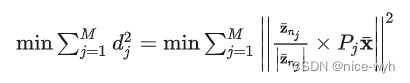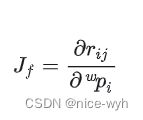VSLAM中的特征点三角化

特征点三角化（Triangulation）是VSLAM中一个非常基础的问题，它是根据特征点在多个相机下的投影恢复出特征点的3D坐标。

特征点在某个相机中被观测到，根据相机位姿和观测向量可以得到3D空间中的一条从相机中心出发的观测“射线”，多个相机位姿观测会产生多条观测射线，理想情况下这些观测射线相交于空间中一点，求所有观测射线的交点就是特征点在3D空间的位置，这就是三角化最朴素的思想。

实际中由于噪声的存在，这些观测射线不可能刚好相交于一点，那如何求特征点坐标呢？有几种思路：

1. 最直觉的思路是：找一个3D点与所有观测射线的距离都很近，以此作为特征点。
2. 另一种思路觉得：误差来源于2D图像观测，所以把特征点投影到每个2D相机平面，最小化所有2D投影点到对应观测点之间的距离（重投影误差）。
3. 第三种思路是：很多时候三角化是在线（Online）运行的，并不是全部观测都拿到以后再进行求解，而是一边获取观测一边估计特征点，所以用一个滤波器来估计特征点的概率分布（通常是Gaussian），旧的观测信息被隐式的存放在概率分布中，来了新的观测后，用新的观测来更新特征点的概率分布，这样能够节省很大的计算量，这就是滤波方法的朴素思想。

 问题定义

设3D特征点p被M个相机观测到，，已知相机位姿，相机内参为K，特征点在个相机的图像观测，求：特征点的3D坐标

不考虑误差的情况有如下投影关系（接下来的方法基本上都会用到该投影关系）：

 

 1.闭式求解

1.1最小化3D距离

最小化3D距离的目标是：在世界坐标系下求一个3D点离所有观测射线的3D距离最近。

先求观测射线的数学方程：将图像观测转为相机坐标系下的单位观测向量，（注意：这里的是单位向量，不是normalize 平面的向量）：

 式中 是观测在normalize平面的齐次坐标，是归一化后的单位方向向量

是齐次坐标。是相机坐标系中的向量，将它转到世界坐标系得到世界系的观测射线方程为：

特征点到射线的距离为： 

 

目标函数定义为特征点到所有观测距离的平方和最小（最小二乘）：

 为了简化求解，令，去掉部分上下标，目标函数变形为

优化问题等价于求线性方程组的最小二乘解：

对于超定方程组Ax=b其最小二乘解为： ，对于上述方程组： 

 

注意： 必须是单位向量而不是normalize平面向量，两个地方用到了该约束：一个是计算特征点到观测射线距离时，另一个是上述推导中求反对称矩阵平方时。 

1.2Direct Linear Transform

设特征点齐次坐标 ，在第 j个相机的图像观测点齐次坐标为 ，投影矩阵为，投影模型如下：

 由可得，将其展开：

得到三个等式方程，但其实第三个方程是前两个方程的线性组合

所以只有两个线性无关的方程，每个相机观测有两个线性方程，将 M个相机观测的约束方程合并得到 2M个线性方程： 

求解齐次方程组解得，由于是齐次坐标，将解的最后一项归一化为1得到特征点坐标。

1.1和1.2介绍了两种方法都是得到最小二乘意义下的闭式解，但解的形式确不一样，根本原因在于它们的目标函数不同，1.1中的目标函数是最小化3D特征点到所有观测射线之间的距离，而DLT用的目标函数是

DLT的目标函数到底优化的是什么？

它的物理意义并不是很直观，为了对比两种方法的区别，暂时忽略内参 K，令 ，则相当于特征点在相机坐标系下的坐标，如果我们在相机坐标系下优化3D特征点到观测射线的距离，则可以得到1.1中目标函数的另一种等价形式：

这时再回过头看DLT的目标函数 ，DLT相当于优化的是相机原点、normalize平面观测点以及特征点三者组成的三角形的面积。当考虑了内参 K以后，DLT的物理意义又变得不明确了。 

2.优化方法

优化方法基本都是最小化重投影误差（图像平面或Normalize平面），当然你也可以优化特征点到观测射线的3D距离，但这个有闭式解，没必要做优化迭代，而优化重投影误差是个非线性优化问题。

先思考一个问题：既然已经有了闭式解法，为什么还要做优化迭代呢？闭式求解它不香吗？

实践证明，闭式求解确实不香，至少没有优化方法香。其实很好理解，我们把最小二乘解理解为将误差项建模为高斯分布情况下的最大似然估计，闭式方法将高斯误差加在特征点到观测射线的距离上，而实际误差来源于图像观测，所以将高斯误差加在图像平面的距离上更符合实际。因此一般做三角化都是先用闭式解得到初始值，然后在此基础上优化重投影误差，以获得比闭式解更高的精度。

优化方法的目标函数为：

其中， 为投影函数，非线性最小二乘优化求解的关键在于推导 相对于特征点 的Jacobian：

得到Jacobian之后，就是常规的非线性最小二乘求解了，常用的方法有高斯牛顿法、LM法、Dogleg法

3.滤波方法

3.1EKF-SLAM

滤波方法将特征点表示成一个概率分布进行估计，通常是Gaussian分布 ，通过相机观测来估计特征的均值和协方差。 与优化方法类似，滤波方法也是推导重投影误差对特征点的Jacobian，但通常相机位姿也是不准的，所以会把相机位姿和特征点放到特征向量中一起估计，也就是EKF-SLAM，这是残差模型中的Jacobian包含两块：重投影误差对相机状态的Jacobian以及对特征状态的Jacobian：

3.2Depth Filter

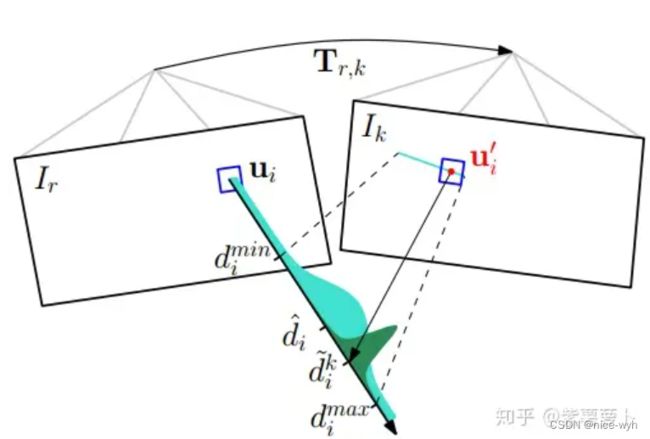
Depth Filter选取一帧图像(通常是第一帧)作为参考帧，然后将特征点坐标表示成，SVO假设参考帧的观测坐标没有误差，这样特征点只取决与深度 d，我们只需要利用其他帧观测来估计 d就好，从而将三维的特征点估计问题转变的一维的深度估计问题。出于一系列考虑，Depth Filter估计的是逆深度 1/d。

逆深度的概率分布建模为一个高斯分布和一个区间均匀分布的加权： 

其中，逆深度为 Z, 内点率为 π, 观测为 x，已知观测 x需要估计 Z,π, 根据Bayes公式得到后验概率:

由于计算复杂，无法直接用上式来迭代计算概率分布，SVO中用Gaussian ×Beta分布来近似：

 然后推导出Gaussian ×Beta分布的迭代公式，迭代公式的推导比较复杂，具体可以参见SVO原文。