还在找数据结构与算法吗?这一篇会满足你!!
一、什么是数据结构?
数据结构思维导图:
![]()
数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。结构包括逻辑结构和物理结构。数据结构是为算法服务的,算法是要作用再特定的数据结构上的。
最常用的数据结构预算法:
数据结构:数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Tire树 算法: 递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
1.1逻辑结构包括4种
(1)集合:数据元素之间除了有相同的数据类型再没有其他的关系
(2)线性结构:数据元素之间是一对一的关系 ——线性表、栈、队列
(3)树形结构:数据元素之间是一对多的关系
(4)图状结构:数据元素之间是多对多的关系。
1.2物理结构包括顺序存储结构和链式存储结构。
顺序存储结构是用一段连续的存储空间来存储数据元素,可以进行随机访问,访问效率较高。链式存储结构是用任意的存储空间来存储数据元素,不可以进行随机访问,访问效率较低
二、五大算法思想
2.1分治策略(快速排序)
把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题,直到最后子问题小到可 以简单的直接求解,原问题的解即子问题的解的合并。这个技巧是很多高效算法的基础,如排序算法(快速排序, 归并排序),傅立叶变换(快速傅立叶变换),大数据中的MR,现实中如汉诺塔游戏。核心思想就是分而治之。 分治法对问题有一定的要求:
-
该问题缩小到一定程度后,就可以轻松解决
-
问题具有可拆解性,不是一团无法拆分的乱麻
-
拆解后的答案具有可合并性。能组装成最终结果
-
拆解的子问题要相互独立,互相之间不存在或者很少有依赖关系
2.2动态规划
基本思想与分治法类似,也是将待求解的问题分解为若干个子问题(阶段),按顺序求解子阶段,前一子问题的解,为后一子问题的求解提供了有用的信息。在求解任一子问题时,列出各种可能的局部解,通过决策保留那些有可能达到最优的局部解,丢弃其他。依次解决各子问题,最后一个子问题就是初始问题的解。动态规划的难点在于寻找动态转换方程式(递归式),一旦找,那么算法已经实现99%。
与分治法最大的不同在于,分治法的思想是并发,动态规划的思想是分步。该方法经分解后得到的子问题往往不是互相独立的,其下一个子阶段的求解往往是建立在上一个子阶段的解的基础上。动态规划算法同样有一定的适用性场景要求:
-
最优化解:拆解后的子阶段具备最优化解,且该最优化解与追踪答案方向一致
-
流程向前,无后效性:上一阶段的解决方案一旦确定,状态就确定,只会影响下一步,而不会反向影响
-
阶段关联:上下阶段不是独立的,上一阶段会对下一阶段的行动提供决策性指导。这不是必须的,但是如果具备该特征,动态规划算法的意义才能更大的得到体现
2.3贪心算法(背包问题)
同样对问题要求作出拆解,但是每一步,以当前局部为目标,求得该局部的最优解。那么最终问题解决时,得到完整的最优解。也就是说,在对问题求解时,总是做出在当前看来是最好的选择,而不去从整体最优上加以考虑。从这一角度来讲,该算法具有一定的场景局限性:
-
要求问题可拆解,并且拆解后每一步的状态无后效性(与动态规划算法类似)
-
要求问题每一步的局部最优,与整体最优解方向一致。至少会导向正确的主方向。
2.4回溯算法
回溯算法实际上是一个类似枚举的搜索尝试过程,在每一步的问题下,列举可能的解决方式。选择某个方案往深度 探究,寻找问题的解,当发现已不满足求解条件,或深度达到一定数量时,就返回,尝试别的路径。回溯法一般适 用于比较复杂的,规模较大的问题。有“通用解题法”之称,回溯就是一种深度优先遍历,先选择一条路走,直到走不通就退回来选择另一条路。(二叉树的遍历)
-
问题的解决方案具备可列举性,数量有限
-
界定回溯点的深度。达到一定程度后,折返
2.5分支限界
与回溯法类似,也是一种在空间上枚举寻找最优解的方式。但是回溯法策略为深度优先。分支法为广度优先。分支 法一般找到所有相邻结点,先采取淘汰策略,抛弃不满足约束条件的结点,其余结点加入活结点表。然后从存活表 中选择一个结点作为下一个操作对象。
三、复杂度分析
3.1复杂度分析用来做什么?
当我们设计一个算法的时候,我们希望让设计的代码运行的更快,更省内存。但是如何考量以上两个指标呢?我们需要通过时间、空间复杂度分析的方式来进行考量。复杂度分析对算法来说非常的重要,也是整个算法学习的精髓。
复杂度也叫渐进复杂度,包括时间复杂度和空间复杂度,用来分析算法执行效率与数据规模之间的增长关系,可以粗略地表示,越高阶复杂度的算法,执行效率越低。常见的复杂度并不多,从低阶到高阶有:O(1)、O(logn)、O(n)、O(nlogn)、O(n2 )。
![]()
3.2为什么要做复杂度分析?
我们做数据分析真的能比把代码跑一遍准确吗?
首先,把代码跑一遍的评估方法是正确的,一些书籍将其称作事后统计法。但是,这些方法拥有局限性。局限性体现在以下方面。
-
测试结果高度依赖于测试环境
-
测试结果受数据规模影响更大
对同一个排序算法,待排序数据的有序度不一样,排序的执行时间就会有很大的差别。(排序算法,如果用例本身有序那么什么都不用做) 如果测试数据规模太小,测试结果可能无法真实地反映算法的性能(比如,对于小规模的数据排序,插入排序可能反倒会比快速排序要快)。 如果测试数据体量太大(达到TB级或者PB级),简单的一个wordCount操作也需要大数据生态的数据处理组件来解决。
3.3复杂度分析表示方法
3.3.1 O复杂度表示法
从CPU的角度看,我们程序的每一行都在执行着读数据-运算-写数据的操作。尽管每行代码对应的cpu的执行个数及时间都不一样,但是由于我们现在讨论的没有那么精准,所以假设每行代码执行时间都一样。我们假设这个值为time。
有段代码用来求数从1到n的累加和,代码如下:
int cal(int n) {
int sum = 0;
int i = 1;
for (; i <= n; ++i) {
sum = sum + i;
}
return sum;
}
由以上代码可以看出,在for循环前的代码每行执行了一遍,在for循环及其中的代码每行执行了n遍,那么总消耗时间为(2+2n)*time,可以看出,所有代码的时间消耗T(n)与每行代码的执行次数成正比(代码行数越多,执行时间越长)。 这种正比的关系,我们可以按照O表示法来表示。
-
n用来表示数据规模的大小
-
f(n)表示代码执行次数的总和
-
O用来表示正比的关系
那么以上代码块的正比关系可以用T(n) = O(2n+2)来表示。
这里的O表示法并不表示代码真正的执行时间,而是表示一种代码执行时间随着数据规模增长的变化趋势,也叫渐进时间复杂度(asymptotic time complexity),简称时间复杂度。 由于公式中的常量、系数和低阶并不左右这种对应关系的增长趋势,所以我们只记一个最大量级即可。即T(n) = O(n)。
3.4 如何分析一段代码的时间复杂度?
3.4.1只关注执行次数最多的一段代码
我们在分析一个算法、一段代码的时间复杂度的时候,也只关注循环执行次数最多的那一段代码就可以了(由于常量,低阶和系数在O时间复杂度表示法中可省略,因为它们量级低,执行次数最多的一段代码才会是高量级)。
3.4.2.加法法则:总复杂度等于量级最大的那段代码的复杂度
执行次数是n次的代码和执行次数是n²的代码在一起,总的复杂度是O(n²)。因为当n无限大的时候,n的时间复杂度可以省略,因为它对正比对应关系的趋势没影响。
加法法则对应成公式的形式:如果 T1(n)=O(f(n)),T2(n)=O(g(n));那么 T(n)=T1(n)+T2(n)=max(O(f(n)), O(g(n))) =O(max(f(n), g(n))).
3.4.3. 乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
3.5常见的复杂度的量级
常见的时间复杂度的量级分为两种:
多项式量级(左侧),这类能找到多项式级时间复杂度的解决算法的问题叫做P(Deterministic )问题 非多项式量级(右侧),这类解决它的时间复杂度为非多项式量级的算法问题叫作 NP(Non-Deterministic Polynomial,非确定多项式)问题。
![]()
3.6复杂度分析的应用–快排
快排核心部分分为三个步骤:
-
找到固定位置(这里取的是left边界的位置)的值(flag)应该放在的位置(当l=r的位置),将小于它的都放左边,大于它的都放右边
-
将找到的位置放入固定值flag
-
递归以上操作,排该位置左边的元素,排该位置右边的元素
class Solution {
public int[] sortArray(int[] nums) {
int left = 0;
int right = nums.length-1;
mySort(nums,left,right);
return nums;
}
private void mySort(int[] nums, int left, int right) {
int l = left;
int r = right;
if(l=flag) r--;
nums[l] = nums[r];
while(l
推导出来的时间复杂度为 O(nlogn)。
四、算法例题
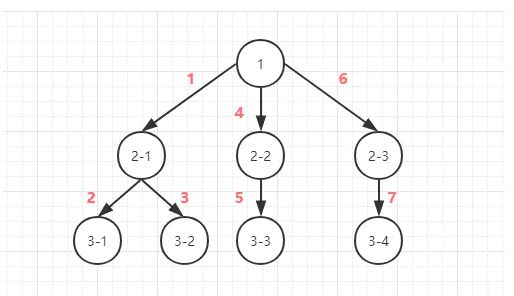
4.1.树的构建与前序遍历
class 二叉树 {
public static void main(String[] args) {
TreeNode node7=new TreeNode(7,null,null);
TreeNode node6=new TreeNode(6,null,null);
TreeNode node5=new TreeNode(5,node6,node7);
TreeNode node4=new TreeNode(4,null,null);
TreeNode node3=new TreeNode(3,null,null);
TreeNode node2=new TreeNode(2,node4,node5);
TreeNode node1=new TreeNode(1,node2,node3);
pp(node1);//前序遍历
}
public static void pp(TreeNode root){
if(root==null){
return;
}
System.out.println(root.val);//前序
pp(root.left);
// System.out.println(root.val);//中序
pp(root.right);
// System.out.println(root.val);//后序
}
public static class TreeNode{
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(){}
public TreeNode(int val){this.val=val;}
public TreeNode(int val,TreeNode left,TreeNode right){
this.val=val;
this.left=left;
this.right=right;
}
}
}
如上图
4.2. 图的深度优先遍历(bfs)
import java.util.Scanner;
public class DFS {
public static boolean visited[] = new boolean[20];//访问标识,数量大于等于最大顶点数
//创建图
public static int[][] createGraph(int n,int v) {
int i,j,w;//边及权值
Scanner scan=new Scanner(System.in);
int Graph[][]=new int[n][n];
for(i=0;i
如上图
4.3.连通图(普利姆算法prim)<最小生成树>
连通图:图的连通其实就是树,图的最小连通图其实就是最小生成树。
public class Graph_1 {
private int vertexSize; // 顶点数量
private int[] vertexs; // 顶点数组
private int[][] matrix; // 邻接矩阵
private static final int MAX_WEIGHT = 1000;
private boolean[] isVisited; // 是否被访问过
public Graph_1(int vertexSize) {
this.vertexSize = vertexSize;
vertexs = new int[vertexSize];
matrix = new int[vertexSize][vertexSize];
for (int i = 0; i < vertexSize; i++) {
vertexs[i] = i;
}
isVisited = new boolean[vertexSize];
}
// prim 普里姆算法
public void prim() {
// 最小代价顶点权值的数组,为0表示已经获取最小权值
int[] lowcost = new int[vertexSize];
// 放顶点权值
int[] adjvex = new int[vertexSize];
int min, minId, sum = 0;
// 把v0数组赋值给lowcost
for (int i = 1; i < vertexSize; i++) {
lowcost[i] = matrix[0][i];
}
// 只是单纯的循环,除此之外没有任何用处
for (int i = 1; i < vertexSize; i++) {
min = MAX_WEIGHT;
minId = 0;
// lowcost数组已更新,所以还要找出lowcost中最小的元素及下标
for (int j = 1; j < vertexSize; j++) {
if (lowcost[j] < min && lowcost[j] > 0) {
min = lowcost[j];
minId = j;
}
}
/**
* 为什么要找到最小元素和下标?
* 因为最小元素代表当前的已知顶点到其它顶点的最短路径,我们要得到这个
* 最短路径通向的顶点。然后周而复始。
* 核心思想:
* 从某一顶点开始,找到该顶点周围的最短路径及此路径通向的顶点。
* 以这两个顶点为准,找到这两个顶点周围的最短路径及此路径通向的顶点。
* ......最终会通过这个"最短路径算法"走完所有的顶点。
// System.out.println("顶点:" + adjvex[minId] + "权值:" + min);
sum += min; // 加权重
lowcost[minId] = 0;
// 在v[minId]中找到比lowcost[]中同等位置小的值
for (int j = 1; j < vertexSize; j++) {
if (lowcost[j] != 0 && matrix[minId][j] < lowcost[j]) {
lowcost[j] = matrix[minId][j];
adjvex[j] = minId;
}
}
}
System.out.println("最小生成树权值和:" + sum);
}
public static void main(String[] args) {
Graph_1 graph = new Graph_1(9);
int[] a1 = new int[] { 0, 10, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 11, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT };
int[] a2 = new int[] { 10, 0, 18, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 16, MAX_WEIGHT, 12 };
int[] a3 = new int[] { MAX_WEIGHT, MAX_WEIGHT, 0, 22, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 8 };
int[] a4 = new int[] { MAX_WEIGHT, MAX_WEIGHT, 22, 0, 20, MAX_WEIGHT, MAX_WEIGHT, 16, 21 };
int[] a5 = new int[] { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 20, 0, 26, MAX_WEIGHT, 7, MAX_WEIGHT };
int[] a6 = new int[] { 11, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 26, 0, 17, MAX_WEIGHT, MAX_WEIGHT };
int[] a7 = new int[] { MAX_WEIGHT, 16, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 17, 0, 19, MAX_WEIGHT };
int[] a8 = new int[] { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 16, 7, MAX_WEIGHT, 19, 0, MAX_WEIGHT };
int[] a9 = new int[] { MAX_WEIGHT, 12, 8, 21, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 0 };
graph.matrix[0] = a1;
graph.matrix[1] = a2;
graph.matrix[2] = a3;
graph.matrix[3] = a4;
graph.matrix[4] = a5;
graph.matrix[5] = a6;
graph.matrix[6] = a7;
graph.matrix[7] = a8;
graph.matrix[8] = a9;
graph.prim();
}
}
如上图
4.4.连通图(克鲁斯卡尔GraphKruskal)<最小生成树>
public class GraphKruskal {
private Edge[] edges;
private int edgeSize; // 边的数量
public GraphKruskal(int edgeSize) {
this.edgeSize = edgeSize;
edges = new Edge[edgeSize];
}
public void miniSpanTreeKruskal() {
int m, n, sum = 0;
int[] parent = new int[edgeSize]; // 神奇的数组,下标为起点,值为终点
for (int i = 0; i < edgeSize; i++) {
parent[i] = 0; 图如上
}
for (int i = 0; i < edgeSize; i++) {
n = find(parent, edges[i].begin);
m = find(parent, edges[i].end);
if (n != m) { // 代表没有回环
parent[n] = m;
System.out.println("起始顶点:" + edges[i].begin + "---结束顶点:" + edges[i].end + "~权值:" + edges[i].weight);
sum += edges[i].weight;
} else {
System.out.println("第" + i + "条边回环了");
}
}
System.out.println("sum:" + sum);
}
//将神奇数组进行查询获取非回环的值
public int find(int[] parent, int f) {
while (parent[f] > 0) { 原理如上图
System.out.println("找到起点" + f);
f = parent[f];
System.out.println("找到终点:" + f);
}
return f;
}
public void createEdgeArray() {
Edge edge0 = new Edge(4, 7, 7);//创建edge边图
Edge edge1 = new Edge(2, 8, 8);
Edge edge2 = new Edge(0, 1, 10);
Edge edge3 = new Edge(0, 5, 11);
Edge edge4 = new Edge(1, 8, 12);
Edge edge5 = new Edge(3, 7, 16);
Edge edge6 = new Edge(1, 6, 16);
Edge edge7 = new Edge(5, 6, 17);
Edge edge8 = new Edge(1, 2, 18);
Edge edge9 = new Edge(6, 7, 19);
Edge edge10 = new Edge(3, 4, 20);
Edge edge11 = new Edge(3, 8, 21);
Edge edge12 = new Edge(2, 3, 22);
Edge edge13 = new Edge(3, 6, 24);
Edge edge14 = new Edge(4, 5, 26);
edges[0] = edge0;
edges[1] = edge1;
edges[2] = edge2;
edges[3] = edge3;
edges[4] = edge4;
edges[5] = edge5;
edges[6] = edge6;
edges[7] = edge7;
edges[8] = edge8;
edges[9] = edge9;
edges[10] = edge10;
edges[11] = edge11;
edges[12] = edge12;
edges[13] = edge13;
edges[14] = edge14;
}
class Edge {
private int begin;
private int end;
private int weight;
public Edge(int begin, int end, int weight) {
super();
this.begin = begin;
this.end = end;
this.weight = weight;
}
}
public static void main(String[] args) {
GraphKruskal graphKruskal = new GraphKruskal(15);
graphKruskal.createEdgeArray();
graphKruskal.miniSpanTreeKruskal();
}
}
矩阵图
思路图
4.5深度优先与广度优先
1.深度优先(DFS)
2.广度优先(BFS)
两者的区别:
对于算法来说 无非就是时间换空间 空间换时间
-
深度优先不需要记住所有的节点, 所以占用空间小, 而广度优先需要先记录所有的节点占用空间大
-
深度优先有回溯的操作(没有路走了需要回头)所以相对而言时间会长一点
深度优先采用的是堆栈的形式, 即先进后出 广度优先则采用的是队列的形式, 即先进先出
4.6普利姆算法与克鲁斯卡尔算法的区别
假设网中有n个节点和e条边
普利姆算法的时间复杂度是O(n^2)
克鲁斯卡尔算法的时间复杂度是O(eloge)
可以看出前者与网中的边数无关
而后者相反
因此
普利姆算法适用于边稠密的网络
克鲁斯卡尔算法适用于求解边稀疏的网