SVM原理理解
目录
概念推导：
共识：距离两个点集距离最大的分类直线的泛化能力更好，更能适应复杂数据。
怎么能让margin最大？
最大化margin公式：
求解最大margin值：
拉格朗日乘子法：
为什么公式中出现求和符号?
SVM模型:
求解拉格朗日乘子：
如何求解？
1.计算实例：
2.求解算法--SMO
求解问题：
工作原理：
为什么每次要选择两个变量来更新，而不是一个变量呢？
代码：
小结：
学习资料：
猫都能看懂的SVM【从概念理解、优化方法到代码实现】_哔哩哔哩_bilibili
不简单的SVM - 知乎 (zhihu.com)
机器学习中的超平面wx+b=0?_平面方程wx+b=0-CSDN博客
优化-拉格朗日乘子法 - 知乎 (zhihu.com)
概念推导：
样本集：
类别标签：
分类直线：
当
时，表示点在分类直线上；
表示该点在直线上方，表示该点为正样本；
表示该点在直线下方，该点为负样本；将上述转化为数学语言，即：
对于二分类问题，我们可以找到许多分类直线将不同点集正确区分。如下图：灰色面中的直线都是分类直线。margin表示间隔。
共识：距离两个点集距离最大的分类直线的泛化能力更好，更能适应复杂数据。
因此我们希望所有的点都被正确分类并且落在两条直线的两侧，且直线内区域尽量大。对上述公式进行改进：即
在（-1，1）时，不分类
怎么能让margin最大？
计算最大间隔：
，
表示分类直线边界上里最佳分类直线距离最近的两点；最大间隔margin为，之间的距离，等于
由直线外一点到直线的距离：直线：
（二维平面上公式：ax+by+c=0 点坐标为（x,y)，二分类散点图上点坐标为（x1,x2)表示不同特征
w和x是矩阵 wx+b=w1x1+w2x2+b。所以直线上点满足w1x1+w2x2+b=0，
机器学习中的超平面wx+b=0?_平面方程wx+b=0-CSDN博客）
得：
又：
得：
最大化margin公式：
, 
, 
求解最大margin值：
求
最小值，需要对求偏导数，令其等于0，得到可能的极值点
对其求偏导（可以看成w可以看成（w1,w2,w3,,,wn）,对求偏导是多元函数求偏导，对wi求偏导）
故：
,
问题转化：求条件下，
的极值->寻找多元函数不等式约束下的极值
拉格朗日乘子法：
优化-拉格朗日乘子法 - 知乎 (zhihu.com)
拉格朗日乘子法（Lagrange multipliers）是一种寻找多元函数在一组约束下的极值的方法。
通过引入拉格朗日乘子，可将有 d个变量与 k 个约束条件的最优化问题转化为具有 d+k个变量的无约束优化问题求解。
即：求f(x)在g(x)<=0的极值点。转化为：求L(x,u)=f(x)+ug(x)（u表示为拉格朗日乘子）的极值点。
求L(x,u)极值点的条件：（KKT条件）
求条件下，的极值，数学语言表示：
![L(w,b,\alpha )=\frac{1}{2}w^{\Gamma }w+\sum \alpha _{i}[1-yi(w^{\Gamma }xi+b)]](http://img.e-com-net.com/image/info8/f31238f90e44494d8c1065251c9c7dcd.png){kind=small}
为什么公式中出现求和符号?
L(x,u)=f(x)+ug(x)中:一个u对应一个x.
L(w,b,a)中w={w1,w2,,,wn},需要对应n个拉格朗日乘子。
KKT条件：
, 
![\alpha _{i}[1-yi(w^{\Gamma }xi+b)]=0](http://img.e-com-net.com/image/info8/2c621e78a3184aebb13385373ce64164.png){kind=small}
注意：对于不在两分类直线上的点（
），
如图所示：
将，
带入
.
得：
.
将，
代入
得：
(
)
由
,
,
得：当
取零时，L取到最大值:
得：
由：
得：
原问题转化：
，
，,
,,
,
SVM模型:
由：
xi表示特征，yi表示标签，均为已知。
是唯一未知数。
且：对于不在两分类直线上的点（），
说明边界外的，对w和b的求解不起作用；在边界上的点X,对w和b的求解有作用，称为支持向量。
求解拉格朗日乘子：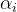
当取值满足：
，时，取到最大间隔margin,此时的直线的拟合效果最好。
如何求解？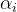
1.计算实例：
6-求解决策方程_哔哩哔哩_bilibili
2.求解算法--SMO
求解问题：
，
工作原理：
1.每次选择满足的两个变量
2.固定以外的参数（固定参数表示，给以外的赋值，只把作为变量。），求解来更新。
为什么每次要选择两个变量来更新，而不是一个变量呢？
，如果我们每次只改变一个，可能不满足
。
代码：
1.数据集创建（和基于Logistic回归实现二分类-CSDN博客中创建的方式相同）
def boolean_int(y):
return [1 if cell else -1 for cell in y]
def createtraindataset():
np.random.seed(0)
n_samples=100
X=np.random.randn(n_samples,2)
y=np.random.randint(2,size=100)
#featur2>2*feature1时 y为1，否则y为-1
y=(X[:,1]>2*X[:,0].astype(int))
train_y=np.array(boolean_int(y)).reshape(100,1)
train_X = X
print("y",train_y)
plt.scatter(X[y==0,0],X[y==0,1],c='r',marker='x',label='Class 1')
plt.scatter(X[y==1,0],X[y==1,1],c='b',marker='o',label='Class -1')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.title("Classification Dataset")
plt.show()
return train_X,train_y2.简化版SMO实现：（详解待续）
#m是a参数的总数，i是第一个ai值，选择第二个aj值
def select_random_index(m, i):
j = i
while j == i:
j = np.random.randint(0, m)
return j
#调整alpha的值
def clip_alpha(alpha, L, H):
if alpha < L:
return L
elif alpha > H:
return H
else:
return alpha
def smo_simple(data, labels, C, tol, max_passes):
m, n = data.shape
alphas = np.zeros(m)
b = 0
passes = 0
while passes < max_passes:
#表示a是否被改变？
num_changed_alphas = 0
for i in range(m):
# 计算损失
Ei = np.dot(alphas * labels, np.dot(data, data[i])) + b - labels[i]
#判断是否a可以被优化
if (labels[i] * Ei < -tol and alphas[i] < C) or (labels[i] * Ei > tol and alphas[i] > 0):
#随机选择aj
j = select_random_index(m, i)
Ej = np.dot(alphas * labels, np.dot(data, data[j])) + b - labels[j]
alpha_i_old, alpha_j_old = alphas[i], alphas[j]
if labels[i] != labels[j]:
L = max(0, alphas[j] - alphas[i])
H = min(C, C + alphas[j] - alphas[i])
else:
L = max(0, alphas[j] + alphas[i] - C)
H = min(C, alphas[j] + alphas[i])
if L == H:
continue
eta = 2 * np.dot(data[i], data[j]) - np.dot(data[i], data[i]) - np.dot(data[j], data[j])
if eta >= 0:
continue
alphas[j] -= labels[j] * (Ei - Ej) / eta
alphas[j] = clip_alpha(alphas[j], L, H)
if abs(alphas[j] - alpha_j_old) < 1e-5:
continue
alphas[i] += labels[i] * labels[j] * (alpha_j_old - alphas[j])
b1 = b - Ei - labels[i] * (alphas[i] - alpha_i_old) * np.dot(data[i], data[i]) - labels[j] * (alphas[j] - alpha_j_old) * np.dot(data[i], data[j])
b2 = b - Ej - labels[i] * (alphas[i] - alpha_i_old) * np.dot(data[i], data[j]) - labels[j] * (alphas[j] - alpha_j_old) * np.dot(data[j], data[j])
if 0 < alphas[i] < C:
b = b1
elif 0 < alphas[j] < C:
b = b2
else:
b = (b1 + b2) / 2
num_changed_alphas += 1
if num_changed_alphas == 0:
passes += 1
else:
passes = 0
return alphas, b
data,labels = createtraindataset()
alphas, b = smo_simple(data, labels, 0.6, 0.001, 40)
print("alphas",alphas,"b",b)
小结：
1.Logistic算法和SVM的区别和联系：
模型不同：、，Logistic模型更简单，SVM更复杂。
决策边界不同，都能解决分类问题：Logistic解决二分类问题，得到分类直线；SVM可以解决二分类，使用间隔最大化确定一个决策面。
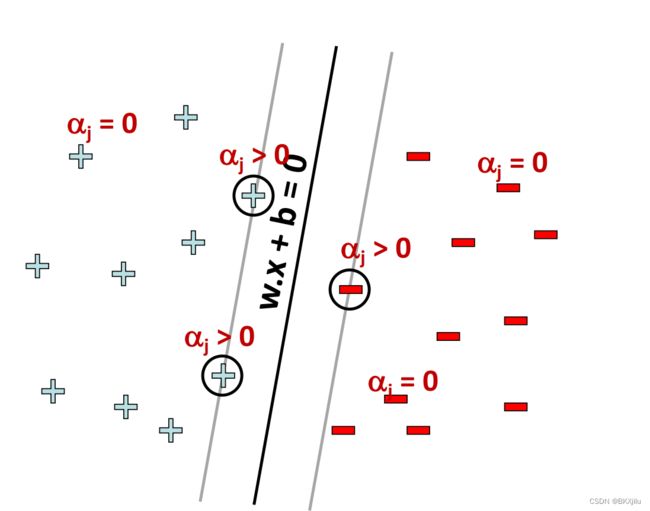
2.上述解释的SVM算法属于硬间隔SVM，在实际应用中可能存在问题：
如下，标圆圈的样本处于决策边界以内，而且难以被决策直线完全区分；这些样本可能是噪声。
就算能够完全可分，也可能出现过拟合。
为了更加符合实际，需要允许少量样本不满足约束。
即：
表示松弛向量,
，
,
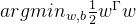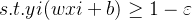
C很大，margin很大，决策面大，分类不太严格；反之分类很严格。