视觉SLAM十四讲 第4讲李群与李代数
目录
- 一、李群与李代数基础
-
- 群
- 李代数的引出
- 李代数的定义
- 李代数 s o ( 3 ) \mathfrak{so} (3) so(3)
- 李代数 s e ( 3 ) \mathfrak{se}(3) se(3)
- 二、指数和对数映射
-
- S O ( 3 ) SO(3) SO(3)上的指数映射
- S E ( 3 ) SE(3) SE(3)上的指数映射
- 三、李代数求导与扰动模型
-
- BCH公式与近似公式
- S O ( 3 ) SO(3) SO(3)李代数上的求导
- 李代数求导
- 扰动模型(左乘)
- S E ( 3 ) SE(3) SE(3)上的李代数求导
一、李群与李代数基础
上一节给出了三维旋转矩阵构成了特殊正交群SO(3),变换矩阵构成了特殊欧式群SE(3),但并未给出群的概念。
群
群是一种集合加上一种运算的代数结构。把集合记作 A A A,运算记为 ⋅ \cdot ⋅,那么群可以记作 G = ( A , ⋅ ) G = (A, \cdot) G=(A,⋅)。群要求运算满足以下几个性质:

而李群是指具有连续光滑性质的群。刚体可以在三维空间内连续运动,故 S O ( 3 ) , S E ( 3 ) SO(3),SE(3) SO(3),SE(3)都是李群。
李代数的引出
对于任意的旋转矩阵 R R R,都满足:
R R T = I (1) RR^T=I \tag{1} RRT=I(1)
用 R R R来表示某个相机的旋转,他是时间的函数,随时间连续变化,即 R ( t ) R(t) R(t),仍然有:
R ( t ) R ( t ) T = I (2) R(t)R(t)^T=I \tag{2} R(t)R(t)T=I(2)
在等式两边同时对时间求导,这里不考虑旋转矩阵的实际意义,而只是把他当做普通矩阵来处理,便于李代数的引出。得到
R ˙ ( t ) R ( t ) T + R ( t ) R ˙ ( t ) T = 0 (3) \dot{R}(t)R(t)^T+R(t)\dot{R}(t)^T=0 \tag{3} R˙(t)R(t)T+R(t)R˙(t)T=0(3)
进而得:
R ˙ ( t ) R ( t ) T = − R ( t ) R ˙ ( t ) T = − ( R ˙ ( t ) R ( t ) T ) T (4) \dot{R}(t)R(t)^T=-R(t)\dot{R}(t)^T=-(\dot{R}(t)R(t)^T)^T \tag{4} R˙(t)R(t)T=−R(t)R˙(t)T=−(R˙(t)R(t)T)T(4)
如果令 W ( t ) = R ˙ ( t ) R ( t ) T W(t) = \dot{R}(t)R(t)^T W(t)=R˙(t)R(t)T,则有 W ( t ) = − W ( t ) T W(t)=-W(t)^T W(t)=−W(t)T,可知 W ( t ) W(t) W(t)为反对称矩阵,进而 R ˙ ( t ) R ( t ) T \dot{R}(t)R(t)^T R˙(t)R(t)T为反对称矩阵。
根据上节使用的符号 ∧ \wedge ∧,他将一个向量转换为一个反对称矩阵,同样,我们定义符号 ∨ \lor ∨他将一个反对称矩阵转换为一个向量。
a ∧ = A = [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] , A ∨ = a (5) a^{\land} = A = \begin{bmatrix} 0 & -a_3 & a_2\\ a_3 & 0 & -a_1\\ -a_2 & a_1 & 0 \end{bmatrix}, A^{\lor} = a \tag{5} a∧=A=⎣⎡0a3−a2−a30a1a2−a10⎦⎤,A∨=a(5)
这样,对于刚刚的反对称矩阵 W ( t ) = R ˙ ( t ) R ( t ) T W(t) =\dot{R}(t)R(t)^T W(t)=R˙(t)R(t)T,就可以找到一个向量 ϕ ( t ) \phi(t) ϕ(t),使得 ϕ ( t ) ∧ = W ( t ) = R ˙ ( t ) R ( t ) T \phi(t)^{\land} = W(t) = \dot{R}(t)R(t)^T ϕ(t)∧=W(t)=R˙(t)R(t)T,即:
R ˙ ( t ) R ( t ) T = ϕ ( t ) ∧ (6) \dot{R}(t)R(t)^T = \phi(t)^{\land} \tag{6} R˙(t)R(t)T=ϕ(t)∧(6)
两边右乘 R ( t ) R(t) R(t),有:
R ˙ ( t ) R ( t ) T R ( t ) = ϕ ( t ) ∧ R ( t ) (7) \dot{R}(t)R(t)^TR(t) = \phi(t)^{\land}R(t) \tag{7} R˙(t)R(t)TR(t)=ϕ(t)∧R(t)(7)
R ˙ ( t ) = ϕ ( t ) ∧ R ( t ) = [ 0 − ϕ 3 ϕ 2 ϕ 3 0 − ϕ 1 − ϕ 2 ϕ 1 0 ] R ( t ) (8) \dot{R}(t) = \phi(t)^{\land}R(t)= \begin{bmatrix} 0 & -\phi_3 & \phi_2\\ \phi_3 & 0 & -\phi_1\\ -\phi_2 & \phi_1 & 0 \end{bmatrix}R(t) \tag{8} R˙(t)=ϕ(t)∧R(t)=⎣⎡0ϕ3−ϕ2−ϕ30ϕ1ϕ2−ϕ10⎦⎤R(t)(8)
可以看出,将旋转矩阵左乘一个 ϕ ( t ) ∧ \phi(t)^{\land} ϕ(t)∧矩阵,相当于旋转矩阵 R ( t ) R(t) R(t)对时间求了一次导数。我们在 t 0 = 0 t_0 = 0 t0=0处,对旋转矩阵 R ( t ) R(t) R(t)进行泰勒展开:
R ( t ) ≈ R ( t 0 ) + R ˙ ( t 0 ) ( t − t 0 ) (9) R(t) \approx R(t_0) + \dot{R}(t_0)(t-t_0) \tag{9} R(t)≈R(t0)+R˙(t0)(t−t0)(9)
假设旋转矩阵在初始状态下有 R ( t 0 ) = R ( 0 ) = I R(t_0)=R(0)=I R(t0)=R(0)=I,则
R ( t ) ≈ R ( t 0 ) + R ˙ ( t 0 ) ( t − t 0 ) = I + R ˙ ( t 0 ) ( t − t 0 ) (10) R(t) \approx R(t_0) + \dot{R}(t_0)(t-t_0) = I+\dot{R}(t_0)(t-t_0) \tag{10} R(t)≈R(t0)+R˙(t0)(t−t0)=I+R˙(t0)(t−t0)(10)
进一步由式8
R ( t ) ≈ I + ϕ ( t 0 ) ∧ I t = I + ϕ ( t 0 ) ∧ ( t ) (11) R(t) \approx I+\phi(t_0)^{\land}It = I + \phi(t_0)^{\land}(t)\tag{11} R(t)≈I+ϕ(t0)∧It=I+ϕ(t0)∧(t)(11)
ϕ \phi ϕ反应了 R R R的导数性质,故称它在 S 0 ( 3 ) S0(3) S0(3)原点附近的正切空间上,在 t 0 t_0 t0附近,假设 ϕ \phi ϕ的值保持常数 ϕ ( t 0 ) = ϕ 0 \phi(t_0)=\phi_0 ϕ(t0)=ϕ0,由式8:
R ˙ ( t ) = ϕ 0 ∧ R ( t ) (12) \dot{R}(t) = \phi_0^{\land}R(t) \tag{12} R˙(t)=ϕ0∧R(t)(12)
这是一个常系数一阶微分方程,根据初始条件 R ( 0 ) = I R(0)=I R(0)=I,得到
R ( t ) = e x p ( ϕ 0 ∧ t ) (13) R(t) = exp(\phi_0^{\land}t) \tag{13} R(t)=exp(ϕ0∧t)(13)
这个式子较为重要
李代数的定义
李代数由一个集合 V \mathbb{V} V,一个数域 F \mathbb{F} F,和一个二元运算符 [ , ] [,] [,]组成,如果满足以下性质,则称 ( V , F , [ , ] ) (\mathbb{V}, \mathbb{F},[,]) (V,F,[,])为一个李代数,记为 g \mathfrak{g} g.
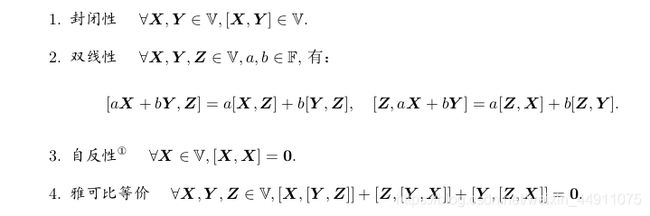
其中的二元运算符称之为李括号。
李代数 s o ( 3 ) \mathfrak{so} (3) so(3)
我们在引出一节中提到的 ϕ \phi ϕ就是一种李代数, S O ( 3 ) SO(3) SO(3)对应的李代数就是定义在 R 3 \mathbb{R}^3 R3上的向量,记作 ϕ \phi ϕ,由上面可知
Φ = ϕ ∧ = [ 0 − ϕ 3 ϕ 2 ϕ 3 0 − ϕ 1 − ϕ 2 ϕ 1 0 ] ∈ R 3 (14) \Phi = \phi^{\land} = \begin{bmatrix} 0 & -\phi_3 & \phi_2\\ \phi_3 & 0 & -\phi_1\\ -\phi_2 & \phi_1 & 0 \end{bmatrix} \in \mathbb{R}^3 \tag{14} Φ=ϕ∧=⎣⎡0ϕ3−ϕ2−ϕ30ϕ1ϕ2−ϕ10⎦⎤∈R3(14)
同时定义两个向量的李括号运算为:
[ ϕ 1 , ϕ 2 ] = ( Φ 1 Φ 2 − Φ 2 Φ 1 ) ∨ (15) [\phi_1, \phi_2] = (\Phi_1\Phi_2-\Phi_2\Phi_1)^{\lor} \tag{15} [ϕ1,ϕ2]=(Φ1Φ2−Φ2Φ1)∨(15)
可以验证该定义下的李括号满足上面提到的几条性质。同时,由于 Φ \Phi Φ和 ϕ \phi ϕ的紧密关系,这两者都可以称之为 s o ( 3 ) \mathfrak{so}(3) so(3)的元素:
s o ( 3 ) = { ϕ ∈ R 3 , Φ = ϕ ∧ ∈ R 3 × 3 } (16) \mathfrak{so}(3)=\{\phi \in \mathbb{R}^3 , \Phi= \phi^{\land} \in \mathbb{R}^{3\times3}\} \tag{16} so(3)={ϕ∈R3,Φ=ϕ∧∈R3×3}(16)
同时根据式13, S O ( 3 ) SO(3) SO(3)和 s o ( 3 ) \mathfrak{so}(3) so(3)的关系也已经给出:
R = e x p ( ϕ ∧ ) (17) R = exp(\phi^{\land}) \tag{17} R=exp(ϕ∧)(17)
李代数 s e ( 3 ) \mathfrak{se}(3) se(3)
对于 S E ( 3 ) SE(3) SE(3)同样由与之对应的李代数,这里直接给出定义:
s e ( 3 ) = { ξ = [ ρ ϕ ] ∈ R 6 , ρ ∈ R 3 , ϕ ∈ s o ( 3 ) , ξ ∧ = [ ϕ ∧ ρ 0 T 0 ] ∈ R 4 × 4 } (18) \mathfrak{se}(3)= \{\xi= \begin{bmatrix} \rho\\ \phi \end{bmatrix} \in \mathbb{R}^6, \rho \in \mathbb{R}^3, \phi \in \mathfrak{so}(3), \xi^{\land} = \begin{bmatrix} \phi^{\land} & \rho\\ 0^T & 0 \end{bmatrix} \in \mathbb{R}^{4\times 4} \} \tag{18} se(3)={ξ=[ρϕ]∈R6,ρ∈R3,ϕ∈so(3),ξ∧=[ϕ∧0Tρ0]∈R4×4}(18)
这里的 ρ \rho ρ可以理解是三维的平移分量,但与实际的三维平移并不相等,还存在一定的关系,将在后面给出。
二、指数和对数映射
S O ( 3 ) SO(3) SO(3)上的指数映射
接下来的问题是考虑 e x p ( ϕ ∧ ) exp(\phi^{\land}) exp(ϕ∧)是怎么计算的。这在李群和李代数中称为指数映射,将其泰勒展开,可以得到:
e x p ( ϕ ∧ ) = ∑ n = 0 ∞ 1 n ! ( ϕ ∧ ) n (19) exp(\phi^{\land}) = \sum^{\infty}_{n=0}\frac{1}{n!}(\phi^{\land})^n \tag{19} exp(ϕ∧)=n=0∑∞n!1(ϕ∧)n(19)
将三维向量 ϕ \phi ϕ拆分成模长和向量乘积的形式,即 ϕ = θ a \mathbf{\phi} = \theta \mathbf{a} ϕ=θa,这里的 a \mathbf{a} a为模长为1的方向向量,对于 a \mathbf{a} a有:
a ∧ a ∧ = a a T − I (20) \mathbf{a}^{\land}\mathbf{a}^{\land}=\mathbf{a}\mathbf{a}^T-\mathbf{I} \tag{20} a∧a∧=aaT−I(20)
a ∧ a ∧ a ∧ = − a ∧ (21) \mathbf{a}^{\land}\mathbf{a}^{\land}\mathbf{a}^{\land}=-\mathbf{a}^{\land} \tag{21} a∧a∧a∧=−a∧(21)
通过上述两条性质,可以得到指数映射的表达:
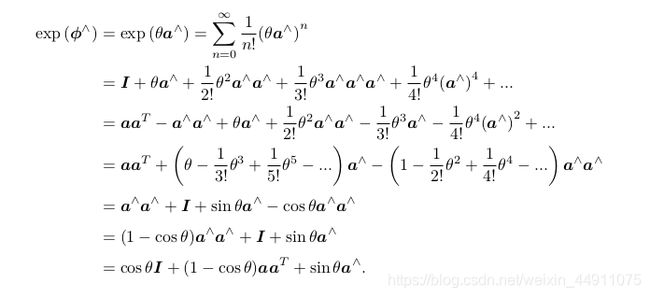
即:
e x p ( ϕ ∧ ) = c o s θ I + ( 1 − c o s θ ) a a T + s i n θ a ∧ (22) exp(\phi^{\land})=cos\theta \mathbf{I}+(1-cos\theta)\mathbf{a}\mathbf{a}^T+sin\theta \mathbf{a}^{\land} \tag{22} exp(ϕ∧)=cosθI+(1−cosθ)aaT+sinθa∧(22)
这与上一节中的罗德里格斯公式如出一辙,可见, S O ( 3 ) SO(3) SO(3)和 s o ( 3 ) \mathfrak{so}(3) so(3)的关系,与旋转矩阵和旋转向量的关系相同。
同理,通过相反的对数映射,也可以将 S O ( 3 ) SO(3) SO(3)映射到 s o ( 3 ) \mathfrak{so}(3) so(3)上:
ϕ = l n ( R ) ∨ = ( ∑ n = 0 ∞ ( − 1 ) n n + 1 ( R − I ) n + 1 ) ∨ (23) \phi=ln(R)^{\lor}=(\sum^{\infty}_{n=0}\frac{(-1)^n}{n+1}(R-I)^{n+1})^{\lor} \tag{23} ϕ=ln(R)∨=(n=0∑∞n+1(−1)n(R−I)n+1)∨(23)
S E ( 3 ) SE(3) SE(3)上的指数映射
我们直接给出映射关系:
e x p ( ξ ∧ ) = [ ∑ n = 0 ∞ 1 n ! ( ϕ ∧ ) n ∑ n = 0 ∞ 1 ( n + 1 ) ! ( ϕ ∧ ) n ρ 0 T 1 ] ≜ [ R J ρ 0 T 1 ] (24) exp(\xi^{\land})= \begin{bmatrix} \sum^{\infty}_{n=0}\frac{1}{n!}(\phi^{\land})^n & \sum^{\infty}_{n=0}\frac{1}{(n+1)!}(\phi^{\land})^n\rho\\ 0^T & 1 \end{bmatrix} \triangleq \begin{bmatrix} \mathbf{R} & \mathbf{J\rho}\\ 0^T & 1 \end{bmatrix} \tag{24} exp(ξ∧)=[∑n=0∞n!1(ϕ∧)n0T∑n=0∞(n+1)!1(ϕ∧)nρ1]≜[R0TJρ1](24)
左上角的 R R R就是 ξ \xi ξ中的 ϕ \phi ϕ分量的指数映射 R R R,之前说过 ρ \rho ρ与真实的平移分量存在特定的关系:
J = s i n θ θ I + ( 1 − s i n θ θ ) a a T + 1 − c o s θ θ a ∧ (25) J=\frac{sin\theta}{\theta}I+(1-\frac{sin\theta}{\theta})aa^T+\frac{1-cos\theta}{\theta}a^{\land} \tag{25} J=θsinθI+(1−θsinθ)aaT+θ1−cosθa∧(25)
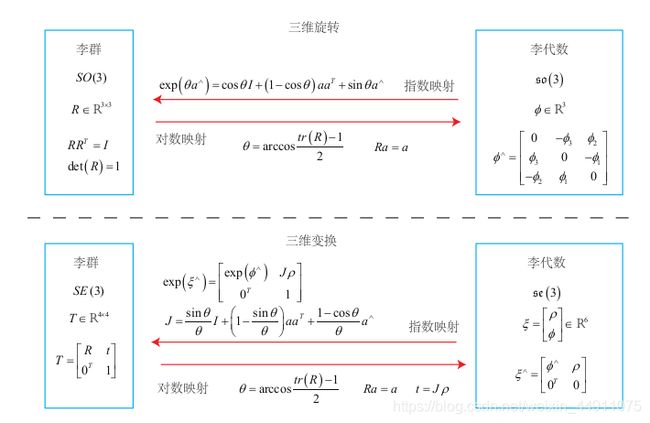
S O ( 3 ) , S E ( 3 ) , s o ( 3 ) , s e ( 3 ) SO(3),SE(3),\mathfrak{so}(3),\mathfrak{se}(3) SO(3),SE(3),so(3),se(3)之间的关系如下:
三、李代数求导与扰动模型
BCH公式与近似公式
我们使用李代数的目的是代替李群来进行优化,因为李群本身所具有的约束会给这一问题带来许多困难。那么现在考虑,当在李群 S O ( 3 ) SO(3) SO(3)上进行两个矩阵的乘法时,在李代数层面,发生了怎样的变化。我们根据指数函数的性质,可能会有这样的猜测:
e x p ( ϕ 1 ∧ ) e x p ( ϕ 2 ∧ ) = e x p ( ( ϕ 1 + ϕ 2 ) ∧ ) (26) exp(\phi_1^{\land})exp(\phi_2^{\land})=exp((\phi_1+\phi_2)^{\land}) \tag{26} exp(ϕ1∧)exp(ϕ2∧)=exp((ϕ1+ϕ2)∧)(26)
但是很遗憾,在标量层面上满足的指数函数性质,在矩阵层面上并不满足,上式并不成立。两个李代数指数映射乘积的完整形式由BCH公式给出,其前几项为:
l n ( e x p ( A ) e x p ( B ) ) = A + B + 1 2 [ A , B ] + 1 12 [ A , [ A , B ] ] − 1 12 [ B , [ A , B ] ] + … (27) ln(exp(A)exp(B))=A+B+\frac12[A,B]+\frac1{12}[A,[A,B]]-\frac1{12}[B,[A,B]]+\dots \tag{27} ln(exp(A)exp(B))=A+B+21[A,B]+121[A,[A,B]]−121[B,[A,B]]+…(27)
但对于 ϕ 1 \phi_1 ϕ1或 ϕ 2 \phi_2 ϕ2位小量时,有如下的近似关系成立:
l n ( e x p ( ϕ 1 ∧ ) e x p ( ϕ 2 ∧ ) ) ∨ ≈ { J l ( ϕ 2 ) − 1 ϕ 1 + ϕ 2 当 ϕ 1 为小量 J r ( ϕ 1 ) − 1 ϕ 2 + ϕ 1 当 ϕ 2 为小量 } (28) ln(exp(\phi_1^{\land})exp(\phi_2^{\land}))^{\lor} \approx \left \{ \begin{aligned} J_l(\phi_2)^{-1}\phi_1+\phi_2 \quad &\text{当$\phi_1$为小量}\\ J_r(\phi_1)^{-1}\phi_2+\phi_1 \quad &\text{当$\phi_2$为小量} \end{aligned} \right\} \tag{28} ln(exp(ϕ1∧)exp(ϕ2∧))∨≈{Jl(ϕ2)−1ϕ1+ϕ2Jr(ϕ1)−1ϕ2+ϕ1当ϕ1为小量当ϕ2为小量}(28)
以第一种情况为例,即在旋转矩阵 R 2 R_2 R2左乘一个微小的旋转矩阵,在李代数层面,这约等于原有李代数 ϕ 2 \phi_2 ϕ2的基础上加上了一项 J l ( ϕ 2 ) − 1 ϕ 1 J_l(\phi_2)^{-1}\phi_1 Jl(ϕ2)−1ϕ1,而这里的 J l J_l Jl实际上就是式25:
J l = s i n θ θ I + ( 1 − s i n θ θ ) a a T + 1 − c o s θ θ a ∧ (29) J_l=\frac{sin\theta}{\theta}I+(1-\frac{sin\theta}{\theta})aa^T+\frac{1-cos\theta}{\theta}a^{\land} \tag{29} Jl=θsinθI+(1−θsinθ)aaT+θ1−cosθa∧(29)
同时也可以得到它的逆:
J l − 1 = θ 2 c o t θ 2 I + ( 1 − θ 2 c o t θ 2 ) a a T − θ 2 a ∧ (30) J_l^{-1}=\frac\theta2cot\frac\theta2I+(1-\frac\theta2cot\frac\theta2)aa^T-\frac\theta2a^{\land} \tag{30} Jl−1=2θcot2θI+(1−2θcot2θ)aaT−2θa∧(30)
还有:
J r ( ϕ ) = J l ( − ϕ ) (31) J_r(\phi) = J_l(-\phi) \tag{31} Jr(ϕ)=Jl(−ϕ)(31)
至此,建立了李群乘法和李代数加法之间的关系。假设有一个旋转 R R R,对应的李代数为 ϕ \phi ϕ,在此旋转基础上左乘一个微小旋转 Δ R \Delta R ΔR,对应的李代数为 Δ ϕ \Delta \phi Δϕ,那么在李群上得到的结果为 Δ R R \Delta R R ΔRR,而在李代数上得到的结果为 J l − 1 ( ϕ ) Δ ϕ + ϕ J_l^{-1}(\phi)\Delta \phi+\phi Jl−1(ϕ)Δϕ+ϕ,有:
e x p ( Δ ϕ ∧ ) e x p ( ϕ ∧ ) = e x p ( ( J l − 1 ( ϕ ) Δ ϕ + ϕ ) ∧ ) (32) exp(\Delta \phi^{\land})exp(\phi^{\land})=exp((J_l^{-1}(\phi)\Delta \phi+\phi)^{\land}) \tag{32} exp(Δϕ∧)exp(ϕ∧)=exp((Jl−1(ϕ)Δϕ+ϕ)∧)(32)
同样,在李代数上进行加法,对应的,在李群上实现了带雅克比的乘法:
e x p ( ( ϕ + Δ ϕ ) ∧ ) = e x p ( ( J l Δ ϕ ) ∧ ) e x p ( ϕ ∧ ) (33) exp((\phi+\Delta \phi)^{\land}) = exp((J_l \Delta \phi)^{\land})exp(\phi^{\land}) \tag{33} exp((ϕ+Δϕ)∧)=exp((JlΔϕ)∧)exp(ϕ∧)(33)
S O ( 3 ) SO(3) SO(3)李代数上的求导
在SLAM中我们要估计一个相机的位置和姿态,该位姿是有 S O ( 3 ) SO(3) SO(3)上的旋转矩阵或 S E ( 3 ) SE(3) SE(3)上的变换矩阵描述的。假设某一时刻机器人的位姿为T,他观察到了一个世界坐标位于 p p p的点,产生了一个观测数据 z z z,由坐标变换关系:
z = T p + w (34) z = Tp+w \tag{34} z=Tp+w(34)
w w w为噪声,正是由于噪声的存在,理想的观测与实际的数据之间往往会存在误差:
e = z − T p (35) e=z-Tp \tag{35} e=z−Tp(35)
假如有N个这样的路标点和观测,对于机器人的位姿估计,相当是寻找一个最优的T,使得整体误差最小化:
min T J ( T ) = ∑ i = 1 N ∣ ∣ z i − T p i ∣ ∣ 2 2 (36) \min_TJ(T) = \sum_{i=1}^N||z_i-Tp_i||_2^2 \tag{36} TminJ(T)=i=1∑N∣∣zi−Tpi∣∣22(36)
这必然需要求解目标函数J对T的导数,而在 S O ( 3 ) SO(3) SO(3)和 S E ( 3 ) SE(3) SE(3)上并没有封闭的加减法,故无法在 S O ( 3 ) SO(3) SO(3)和 S E ( 3 ) SE(3) SE(3)上进行直接求导。若将T当做普通矩阵处理,由于欠封闭性,势必需要加以约束。而可以从李代数的层面解决求导问题。
李代数求导
用李代数来表示姿态,然后用李代数的加法来对李代数进行求导:
空间一点坐标为p,旋转变换为R,对应的李代数为 ϕ \phi ϕ,旋转之后点的坐标相对于旋转本身的导数:
∂ ( R p ) ∂ R = ∂ ( e x p ( ϕ ∧ ) p ) ∂ ϕ (37) \frac{\partial{(Rp)}}{\partial{R}}= \frac{\partial{(exp(\phi^{\land})p)}}{\partial \phi} \tag{37} ∂R∂(Rp)=∂ϕ∂(exp(ϕ∧)p)(37)
有:
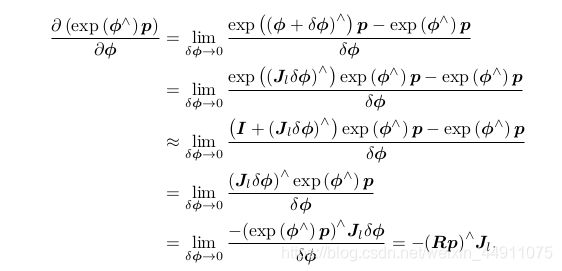
进而得:
∂ ( R p ) ∂ R = ( − R p ) ∧ J l (38) \frac{\partial{(Rp)}}{\partial{R}}=(-Rp)^{\land}J_l \tag{38} ∂R∂(Rp)=(−Rp)∧Jl(38)
这个结果并不是很好,含有J较为复杂。
扰动模型(左乘)
对R进行一次扰动 Δ R \Delta R ΔR,对应的李代数为 Δ φ \Delta \varphi Δφ,以左乘为例:
∂ ( R p ) ∂ φ = lim φ → 0 exp ( φ ∧ ) exp ( ϕ ∧ ) p − exp ( ϕ ∧ ) p φ (39) \frac{\partial{(Rp)}}{\partial\varphi} = \lim_{\varphi \to0}\frac{\exp(\varphi^{\land})\exp(\phi^{\land})p-\exp(\phi^{\land})p}{\varphi} \tag{39} ∂φ∂(Rp)=φ→0limφexp(φ∧)exp(ϕ∧)p−exp(ϕ∧)p(39)
对 exp ( φ ∧ ) \exp(\varphi^{\land}) exp(φ∧)进行泰勒展开,取前两项:
exp ( φ ∧ ) ≈ I + φ ∧ (40) \exp(\varphi^{\land}) \approx I+ \varphi^{\land} \tag{40} exp(φ∧)≈I+φ∧(40)
带回:
∂ ( R p ) ∂ φ = lim φ → 0 ( I + φ ∧ ) exp ( ϕ ∧ ) p − exp ( ϕ ∧ ) p φ = lim φ → 0 φ ∧ exp ( ϕ ∧ ) p φ = lim φ → 0 φ ∧ R p φ = lim φ → 0 − ( R p ) ∧ φ φ = − ( R p ) ∧ (41) \begin{aligned} \frac{\partial{(Rp)}}{\partial\varphi} &= \lim_{\varphi \to0}\frac{(I+ \varphi^{\land})\exp(\phi^{\land})p-\exp(\phi^{\land})p}{\varphi}\\ &=\lim_{\varphi \to 0}\frac{\varphi^{\land}\exp(\phi^{\land})p}{\varphi} =\lim_{\varphi \to 0}\frac{\varphi^{\land}Rp}{\varphi}\\ &=\lim_{\varphi \to 0}\frac{-(Rp)^{\land}\varphi}{\varphi}=-(Rp)^{\land} \end{aligned} \tag{41} ∂φ∂(Rp)=φ→0limφ(I+φ∧)exp(ϕ∧)p−exp(ϕ∧)p=φ→0limφφ∧exp(ϕ∧)p=φ→0limφφ∧Rp=φ→0limφ−(Rp)∧φ=−(Rp)∧(41)
这次的形式要简洁的多。
S E ( 3 ) SE(3) SE(3)上的李代数求导
设点p经过一次变换T对应李代数为 ξ \xi ξ得到Tp,现在给T左乘一个扰动 Δ T = exp ( δ ξ ∧ ) \Delta T= \exp(\delta\xi^{\land}) ΔT=exp(δξ∧),设扰动项的李代数为 δ ξ = [ δ ρ , δ ϕ ] T \delta\xi=[\delta \rho, \delta\phi]^{T} δξ=[δρ,δϕ]T,有:
∂ ( T p ) ∂ δ ξ = [ I − ( R p + t ) ∧ 0 T 0 T ] ≜ ( T p ) ⊙ (42) \frac{\partial{(Tp)}}{\partial \delta\xi}= \begin{bmatrix} I & -(Rp+t)^{\land}\\ 0^T & 0^T \end{bmatrix} \triangleq(Tp)^{\odot} \tag{42} ∂δξ∂(Tp)=[I0T−(Rp+t)∧0T]≜(Tp)⊙(42)
定义运算符 ⊙ \odot ⊙,把一个齐次坐标的空间点转换成一个 4 × 6 4\times 6 4×6的矩阵
往期链接
视觉SLAM十四讲 第3讲 三维空间刚体运动
视觉SLAM十四讲 第2讲 初识slam