莫队（普通莫队，带修莫队，树上莫队）

0. 听说 莫队算法是一种“优雅的暴力”（小声bb）。

---

普通莫队

1/ 引入

problem：给你一个长度为n的数组，有m次查询，每次查询询问一个区间[L, R]内有多少个不同的数。

1. 首先想想暴力怎么做。
   开一个数组用来记数，然后扫一遍[L,R]，如果这个数是第一次出现，那么对答案贡献+1。暴力出来的时间复杂度是O(n*m)，如果n、m较大，那暴力肯定是不行的。
2. 再想想进一步优化。
   开两个指针 l 和 r，将之前的每次扫区间[L,R]改成移动指针l、r，使得指针与区间边界对齐。在移动指针的时候，对应地去删除或添加对答案的贡献即可。但问题来了，如果每次询问的区间[L,R]都需要移动很长的距离，就比如第一次询问[1,2]，第二次询问[n-1,n]，这么一来时间复杂度依旧是O(n*m)。优化了个寂寞

---

2/ 莫队算法的实现

• 回到刚才的第二种思路，我们可不可以在原来的基础上，对左区间进行排序以保证指针l不会移动到曾经被左指针扫过的地方，思想是好的，但是不能确保指针r的移动不重复，所以还是不行。

这个时候就需要莫队算法了。它的核心是分块和排序：将长度为n的数组分为若干个块，每个块内有sqrt(n)个元素，再将每个块按顺序编号，然后排序（对于区间左端点来说，如果在同一个块内，就按右端点排序，否则按左端点排序）。时间复杂度是O(n^1.5)，优化了很大一部分。详细的时间复杂度证明可自行百度

另外多数莫队题的输入输出量是比较大的，用cin大概率会tle，老老实实用scanf或者快读吧。

如果足够细心应该会注意到，对要询问的区间进行排序，那将会打乱原有的询问顺序。换而言之，必须要先输入所有询问，再一次性输出所有对应的答案，也就是我们通常所说的离线操作

---

Code

数据说明：

• e[ ].l ：询问的左端点。 e[ ].r ：询问的右端点。 e[ ].id ：询问的次序。
• size ：每个区间的大小，即 sqrt(n)。
• cnt[i] ：记 i 出现的次数。
• belong[i] ：记 i 属于的块的编号，即 i/size。

---

1. 结构体排序（未优化）：

bool cmp(node x, node y) {
	if (belong[x.l] == belong[y.l]) return x.r < y.r;
	return x.l < y.l;
}

2. .结构体排序（优化后）：

bool cmp(node x, node y) {
	return belong[x.l]^belong[y.l] ? x.l < y.l : (belong[x.l]&1)? x.r < y.r : x.r > y.r;
}

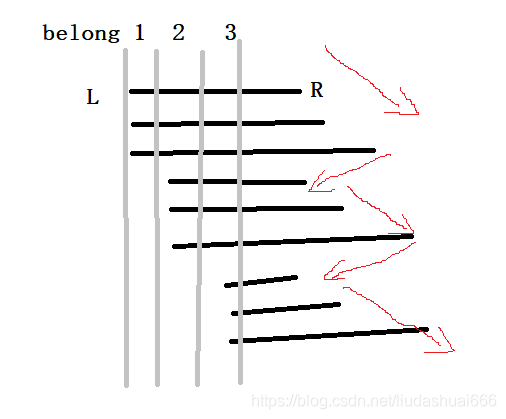
首先用位运算代替了if，这样会快些。另外对于左端点在同一奇数块的区间，右端点按升序排列，反之降序（不论奇数升序偶数降序、还是偶数升序奇数降序 其实都是不影响优化后的复杂度的），时间大概能优化一半吧，至于奇偶排序具体原理嘛。。。简单来说， emm还是画个图吧（灵魂画手show time）

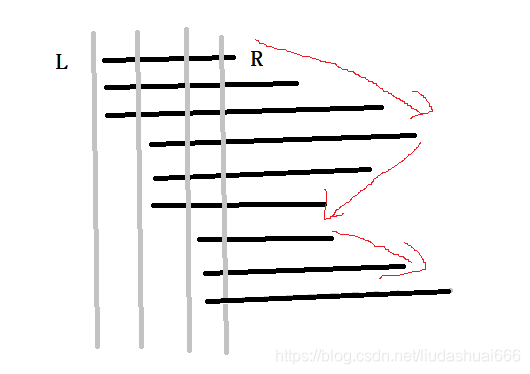
这里R指针的移动是上下上下上，这是按照R升序排列的，那按照奇偶排列的话，那就是这样的：

R指针只需要上下上就完成了，就相当于把两个波峰合并成了一个波峰，那么扫过的路径就会减少大致一半，从而优化了近一半的时间。

完整代码：

const int maxn = 1e6+5;

struct node {
	int l, r, id;
}e[maxn];
int n, m, size, l, r;
ll a[maxn], ans[maxn], cnt[maxn], sum;
int belong[maxn];

// 优化 
bool cmp(node x, node y) {
	return belong[x.l]^belong[y.l] ? x.l < y.l : (belong[x.l]&1)? x.r < y.r : x.r > y.r;
}
/* 
bool cmp(node x, node y) {
	if (belong[x.l] == belong[y.l]) return x.r < y.r;
	return x.l < y.l;
}
*/ 

void add(int pos) {
	if (!cnt[a[pos]]) sum++;
	cnt[a[pos]]++;
}
void del(int pos) {
	cnt[a[pos]]--;
	if (!cnt[a[pos]]) sum--;
}
int main() {
	read(n);
	size = sqrt(n);
	for (int i = 1; i <= n; i++) {
		read(a[i]);
		belong[i] = (i-1)/size;
	} 
	read(m);
	for (int i = 1; i <= m; i++) {
		read(e[i].l), read(e[i].r);
		e[i].id = i;
	}
	sort(e+1, e+1+m, cmp);
	l = 1, r = 0, sum = 0;
	for (int i = 1; i <= m; i++) {
		while (l < e[i].l) del(l++);
		while (l > e[i].l) add(--l);
		while (r < e[i].r) add(++r);
		while (r > e[i].r) del(r--);
		ans[e[i].id] = sum;
	}
	for (int i = 1; i <= m; i++) {
		cout << ans[i] << endl;
	}
	return 0;
}

---

带修莫队

1/ 引入

• 前面说过莫队算法是离线算法，按理来说，输入的数据是不能修改的，但是对于一些允许离线的需要修改区间的查询来说，带修莫队也是可以解决的。

2/ 带修莫队的实现

其实和普通莫队差不多，之前不是用到了指针L，R嘛，带修莫队的区别就在于加了一个维度------时间。
如果不修改的话，就沿用之前的时间戳；修改的话时间戳++，并记录修改的信息。进行查询操作时，通过移动time、L和R指针，使得当前区间与所查询区间的左右端点、时间戳均相同，所得即答案。
说白了就是在之前[l,r+1]、[l,r-1]、[l+1,r]、[l-1,r] （时间戳不变）的基础上，再加两个[l,r,t+1]、[l,r,t-1]就行了。
至于排序嘛，升序排列，优先级是L，R，time。

• 当修改后，有可能要改回来，所以还要记录好原来的值。但其实也可以不存，只要在修改后把修改的值和原值交换一下，那么改回来时也只要交换一下，两次交换后不就相当于还原了嘛。

还有一点就是关于块的大小，经过证明，当块的大小为(n^4*t)的立方根时复杂度最优。块的大小可以取pow(n,2.0/3.0)，那么时间复杂度为pow(n,5.0/3.0) 。这个时间还能接受吧。

Code

const int maxn = 2e6+5;
int n, m, siz, cntq, cntc, now, t, l, r;
int a[maxn], belong[maxn], ans[maxn], cnt[maxn]; 

struct node1 {
	int l, r, id, tim;
}e[maxn];
struct node2 {
	int pos, val;
}c[maxn];

bool cmp(node1 x, node1 y) {
	return (belong[x.l]^belong[y.l]) ? x.l<y.l : (belong[x.r]^belong[y.r]) ? x.r < y.r : x.tim < y.tim;
}

void add(int x) {
	if (!cnt[a[x]]) now++;
	cnt[a[x]]++;
}
void del(int x) {
	cnt[a[x]]--;
	if (!cnt[a[x]]) now--;
}

int main() {
	read(n), read(m);
	siz = pow(n, 2.0/3);
	for (int i = 1; i <= n; i++) {
		read(a[i]);
		belong[i] = (i-1)/siz;
	}
	cntq = cntc = now = 0;
	for (int i = 1; i <= m; i++) {
		char op[50];
		scanf("%s", op);
		if (op[0] == 'Q') {
			read(e[++cntq].l);
			read(e[cntq].r);
			e[cntq].id = cntq;
			e[cntq].tim = cntc;
		} else {
			read(c[++cntc].pos);
			read(c[cntc].val);
		}
	}
	sort(e+1, e+1+cntq, cmp);
	
	l = 1, r = 0, t = 0;
	for (int i = 1; i <= cntq; i++) {
		while (l < e[i].l) del(l++);
		while (l > e[i].l) add(--l);
		while (r < e[i].r) add(++r);
		while (r > e[i].r) del(r--);
		while (t < e[i].tim) {
			t++;
			if (e[i].l <= c[t].pos && c[t].pos <= e[i].r) {
				del(c[t].pos);
				if (!cnt[c[t].val]) now++;
				cnt[c[t].val]++;
			}
			swap(a[c[t].pos], c[t].val);
		}
		while (t > e[i].tim) {
			if (e[i].l <= c[t].pos && c[t].pos <= e[i].r) {
				del(c[t].pos);
				if (!cnt[c[t].val]) now++;
				cnt[c[t].val]++;				
			}
			swap(a[c[t].pos], c[t].val);
			t--;
		}
		ans[e[i].id] = now;
	}
	for (int i = 1; i <= cntq; i++) {
		cout << ans[i] << endl;
	}
	return 0;
}

树上莫队

1/ 引入

• 适用通常是：给你一棵树，求点u到v之间有多少个不同的数。

2/ 树上莫队的实现

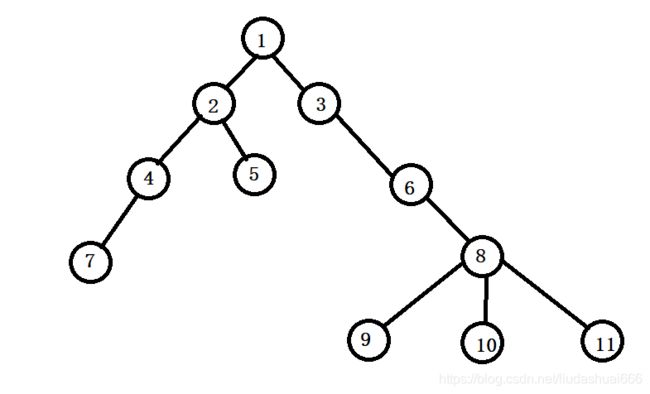
首先介绍欧拉序

对于这棵树，对应的欧拉序是：1 2 4 7 7 4 5 5 2 3 6 8 9 9 10 10 11 11 8 6 3 1
对照一下图和序列，应该不难知道欧拉序的定义。

经过仔细的观察，不难发现 （直接上结论吧还是）

树的欧拉序上两个相同编号（设为x）之间的所有编号都出现两次，且都位于x子树上

（先假设你会求LCA，具体怎么求后面会讲）
那么假设设每个点（编号为a）首次出现的位置first[a]，最后出现的位置为last[a]，那么对于路径u→v，不妨默认first[u]<=first[v]（不满足的话交换就好了，这个操作的意义在于，如果u、v在一条链上，则u一定是v的祖先或等于v），相当于免去了分类讨论嘛。如果lca(u,v)=u，则直接查询[first[u],first[v]]；否则查询[last[u],first[v]]区间，但这个区间是不包含u和v的LCA的，只需要在查询的时候额外加上即可，这样一来就把树上的问题转换成了区间问题，接下来就成了普通莫队啦。

Code

const int maxn = 1e5+5;
int n, m, id, cntn, now;
int a[maxn], head[maxn], val[maxn], tmp[maxn], fir[maxn], las[maxn], ord[maxn], vis[maxn], f[maxn][30], dep[maxn], belong[maxn], cnt[maxn], ans[maxn];
// ord[]---欧拉序

struct node {
	int to, nex;
}e[maxn];
void addedge(int u, int v) { 
	e[++id].to = v;
	e[id].nex = head[u];
	head[u] = id;
}

void dfs(int x) {
	ord[++cntn] = x;
	fir[x] = cntn;
	for (int i = head[x]; i != -1; i = e[i].nex) {
		int to = e[i].to;
		if (to != f[x][0]) {
			dep[to] = dep[x] + 1;
			f[to][0] = x;
			for (int j = 1; (1 << j) <= dep[to]; j++) 
				f[to][j] = f[f[to][j-1]][j-1];
			dfs(to);
		}
	}
	ord[++cntn] = x;
	las[x] = cntn;
}

int LCA(int u, int v) { // LCA后面会有讲解
	if (dep[u] < dep[v]) swap(u, v);
	for (int i = 20; i >= 0; i--)
		if (dep[f[u][i]] >= dep[v])
			u = f[u][i];
	if (u == v) return u;
	for (int i = 20; i >= 0; i--) {
		if (f[u][i] != f[v][i]) {
			u = f[u][i];
			v = f[v][i];
		}
	}
	return f[u][0];
}

struct node2 {
	int l, r, id, lca;
}q[maxn];
int cmp(node2 x, node2 y) {
	return (belong[x.l]^belong[y.l]) ? x.l < y.l : (belong[x.l]&1) ? x.r < y.r : x.r > y.r;  
}

void work(int pos) { //通过忽略走过两遍的点（欧拉序的特性）
	vis[pos] ? now -= !(--cnt[val[pos]]) : now += !(cnt[val[pos]]++);
	vis[pos] ^= 1;
}

int main() {
	read(n), read(m);
	mem(head, -1);
	for (int i = 1; i <= n; i++) read(val[i]), tmp[i] = val[i];
	sort(tmp+1, tmp+1+n);
	// 数据范围大，需要离散化
	int tot = unique(tmp+1, tmp+1+n) - tmp-1;
	for (int i = 1; i <= n; i++) {
		val[i] = lower_bound(tmp+1, tmp+tot+1, val[i]) - tmp;
	}
	for (int k = 1; k < n; k++) {
		int u, v;
		read(u), read(v);
		addedge(u, v);
		addedge(v, u);
	}
	dep[1] = 1;
	dfs(1);
	int siz = sqrt(cntn);
	for (int i = 1; i <= cntn; i++) {
		belong[i] = (i-1)/siz;
	}
	for (int i = 1; i <= m; i++) {
		int l, r, lca;
		read(l);
		read(r);
		lca = LCA(l, r);
		if (fir[l] > fir[r]) swap(l, r);
		if (l == lca) {
			q[i].l = fir[l];
			q[i].r = fir[r];
		} else {
			q[i].l = las[l];
			q[i].r = fir[r];
			q[i].lca = lca;
		}
		q[i].id = i;
	}
	sort(q+1, q+1+m, cmp);
	int l = 1, r = 0;
	for (int i = 1; i <= m; i++) {
		int ql = q[i].l, qr = q[i].r, qlca = q[i].lca;
		while (l < ql) work(ord[l++]);
		while (l > ql) work(ord[--l]);
		while (r < qr) work(ord[++r]);
		while (r > qr) work(ord[r--]);
		if (qlca) work(qlca); //lca不在序列内
		ans[q[i].id] = now;
		if (qlca) work(qlca); //还原
	}
	for (int i = 1;i <= m; i++) {
		cout << ans[i] << endl;
	}
	
	return 0;
}