HDU 1695 GCD 欧拉函数+容斥定理 || 莫比乌斯反演

GCD

Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 4141    Accepted Submission(s): 1441

Problem Description

Given 5 integers: a, b, c, d, k, you're to find x in a...b, y in c...d that GCD(x, y) = k. GCD(x, y) means the greatest common divisor of x and y. Since the number of choices may be very large, you're only required to output the total number of different number pairs.
Please notice that, (x=5, y=7) and (x=7, y=5) are considered to be the same.

Yoiu can assume that a = c = 1 in all test cases.

 

 

Input

The input consists of several test cases. The first line of the input is the number of the cases. There are no more than 3,000 cases.
Each case contains five integers: a, b, c, d, k, 0 < a <= b <= 100,000, 0 < c <= d <= 100,000, 0 <= k <= 100,000, as described above.

 

 

Output

For each test case, print the number of choices. Use the format in the example.

 

 

Sample Input

2

1 3 1 5 1

1 11014 1 14409 9

Sample Output

Case 1: 9

Case 2: 736427

  1 /*

  2 题意：区间x属于[1,A] ， y属于区间[1,B]

  3       求最大公约数是K，即gcd(x,y)=K。

  4       并且[1,3]和[3,1]属于同一种情况。

  5       

  6 思路：HDU 4135 Co-prime 的思路在这一题有用。

  7       它的题意：区间[A,B],与整数N的互素的个数

  8       对于这一到题目：gcd(x,y)=k.

  9       要满足最大公约数是K，可以转化为

 10       [1,A],[1,B]==>[1,A/K],[1,B/K] 求互素的个数。

 11       好像有点难以想到。？？？？

 12       {{

 13       借鉴一下别人是说法。会更明白

 14       gcd(x, y) == k 说明x,y都能被k整除,但是能被k整除的未必gcd=k , 

 15       必须还要满足互质关系. 

 16       问题就转化为了求1~a/k 和 1~b/k间互质对数的问题

 17       }}

 18       这样的话，如何处理呢？

 19       题意要求[1,3]和[3,1]不能重复。

 20       对于区间[1,A/K],[1,B/K] 看成==>[1,a],[1,b] 有几种情况

 21       1____________a

 22       1____________________b

 23       

 24       

 25       1____________a

 26       1________b

 27       

 28       

 29       1____________a

 30       1____________b

 31       

 32       这三种情况。我们来个判断，总是让a<=b，用b做更大的值。就会变成

 33       

 34       1—————————a

 35       1—————————————————b

 36       在求取的过程中也是采取这样的规则。

 37       [?,b1];确定后一位数。表示在[1,a]中与b1互质的个数。

 38       那么就很好的避免了[1,3],[3,1]的情况了。

 39 求取总和sum=sum1+sum2；

 40 sum1=欧拉函数值[1,a]; 想想为什么？

 41 sum2={枚举a+1--->b,与区间[1,a]互质的个数}; 

 42 sum2就和以前的一题有关系了，要用欧拉函数+容斥定理处理。

 43 具体的参考：http://www.cnblogs.com/tom987690183/p/3246197.html

 44 

 45 

 46 */

 47 

 48 #include<stdio.h>

 49 #include<string.h>

 50 #include<stdlib.h>

 51 

 52 

 53 int prime[100003],len;

 54 bool s[100003];

 55 int opl[100003];

 56 int Que[100003];

 57 int f[1000],flen;

 58 

 59 void make_prime() //素数打表

 60 {

 61     int i,j;

 62     len=0;

 63     for(i=2;i<=100000;i++)//刚开始写错，i*i<=100000;⊙﹏⊙b汗

 64     if(s[i]==false)

 65     {

 66         prime[++len]=i;

 67         for(j=i*2;j<=100000;j=j+i)

 68         s[j]=true;

 69     }

 70 }

 71 

 72 void make_Euler() //欧拉函数打表。

 73 {

 74     int i,j;

 75     make_prime();

 76     for(i=2;i<=100000;i++)

 77     opl[i]=i;

 78     opl[1]=1;

 79     for(i=1;i<=len;i++)

 80     for(j=prime[i];j<=100000;j=j+prime[i])

 81     opl[j]=opl[j]/prime[i]*(prime[i]-1);

 82 }

 83 

 84 void make_dEuler(int n) //单点欧拉的素因子。

 85 {

 86     int i;

 87     flen=0;

 88     for(i=2;i*i<=n;i++)

 89     {

 90         if(n%i==0)

 91         {

 92             while(n%i==0)

 93             n=n/i;

 94             f[++flen]=i;

 95         }

 96     }

 97     if(n!=1)

 98     f[++flen]=n;

 99 }

100 

101 int Capacity(int m)

102 {

103     int i,j,t=0,sum=0,k;

104     Que[t++]=-1;

105     for(i=1;i<=flen;i++)

106     {

107         k=t;

108         for(j=0;j<k;j++)

109         Que[t++]=-1*Que[j]*f[i];

110     }

111     for(i=1;i<t;i++)

112     sum=sum+m/Que[i];

113     return sum;

114 }

115 

116 

117 void sc()//输出函数，测试用的。

118 {

119     int i;

120     for(i=1;i<=10;i++)

121     printf("%d ",opl[i]);

122     printf("\n");

123 }

124 

125 __int64 make_ini(int b,int c,int k)

126 {

127     int i,x,y,tmp;

128     __int64 sum=0;

129     x=b/k;y=c/k;//加特判的用处。不能除0

130     if(x>y)

131     {

132         tmp=x;

133         x=y;

134         y=tmp;

135     }

136     for(i=1;i<=x;i++)

137     sum=sum+opl[i];//第一步

138     for(i=x+1;i<=y;i++)//第二步，枚举

139     {

140         make_dEuler(i);

141         sum=sum+(x-Capacity(x));

142     }

143     //sc();

144     return sum;

145 

146 }

147 

148 int main()

149 {

150     int T,a,b,c,d,k,i;

151     __int64 sum;

152     make_Euler();

153     while(scanf("%d",&T)>0)

154     {

155         for(i=1;i<=T;i++)

156         {

157             sum=0;

158             scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);

159             if(k==0) //特判，否则会Runtime Error (INTEGER_DIVIDE_BY_ZERO)

160             {

161                 sum=0;

162             }

163             else sum=make_ini(b,d,k);

164             printf("Case %d: %I64d\n",i,sum);

165 

166         }

167     }

168     return 0;

169 }

 

下面再介绍一种方法。莫比乌斯反演

GCD(a,b) = d;

可以转化为

GCD(a/d,b/d) = 1;

设f(d)为(a,b) = d的种类数

   F(d)为(a,b) = d 的倍数 的种类数。

例如

F(2) = (a/2)*(b/2);

F(3) = (a/3)*(b/3);

由

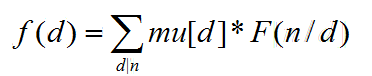
mu[i]可以打表求出。

关于一个优化在于a/i = a/(i+k) && b/i = b/(i+k);

此时我们能节省时间来求。详见代码部分

 1 #include<iostream>

 2 #include<stdio.h>

 3 #include<cstring>

 4 #include<cstdlib>

 5 using namespace std;

 6 typedef __int64 LL;

 7 

 8 const int maxn = 1e5+3;

 9 bool s[maxn];

10 int prime[maxn],len = 0;

11 int mu[maxn];

12 int sum1[maxn];

13 void  init()

14 {

15     memset(s,true,sizeof(s));

16     mu[1] = 1;

17     for(int i=2;i<maxn;i++)

18     {

19         if(s[i] == true)

20         {

21             prime[++len]  = i;

22             mu[i] = -1;

23         }

24         for(int j=1;j<=len && (long long)prime[j]*i<maxn;j++)

25         {

26             s[i*prime[j]] = false;

27             if(i%prime[j]!=0)

28                 mu[i*prime[j]] = -mu[i];

29             else

30             {

31                 mu[i*prime[j]] = 0;

32                 break;

33             }

34         }

35     }

36     for(int i=1;i<maxn;i++)

37         sum1[i] = sum1[i-1]+mu[i];

38 }

39 LL solve(int a,int b)

40 {

41     LL sum = 0;

42     for(int i=1,la = 0;i<=a;i++,i = la+1)

43     {

44         la = min(a/(a/i),b/(b/i)); //优化部分

45         sum = sum + ((LL)(a/i))*(b/i)*(sum1[la]-sum1[i-1]);

46     }

47     return sum;

48 }

49 int main()

50 {

51     int T,l,a,b,d;

52     init();

53     scanf("%d",&T);

54     for(int t=1;t<=T;t++)

55     {

56         scanf("%d%d%d%d%d",&l,&a,&l,&b,&d);

57         LL sum = 0 ;

58         if(d==0) ;

59         else{

60             if(a>b) swap(a,b);

61             sum = solve(a/d,b/d);

62             sum = sum - solve(a/d,a/d)/2;

63         }

64         printf("Case %d: %I64d\n",t,sum);

65     }

66     return 0;

67 }