Algorithm- Insertion Sort

　　The analysis of algorithm is the theoretical study of computer program performance and resource usage. And particular(尤其) performance.

　　Question: in programming, what’s more important than performance? 

　　Answer::Simple、Maintainability(可维护的)、Stability、Functionality、security、Scalability(可扩展的)、User-friendless

　　Question: Why study algorithm performance?

　　Answer: One is performance is measure the line between the feasible and the infeasible(不可行). Another thing is that algorithm give you a language for taking about program behavior.
 

Insertion Sort

Input a sequence <a1,a2,a3...an> of numbers

Output Permutation (排序) <a1,a2,a3....an>

such as

a1<=a2<=a3....<=an

How can I do that? We can use Insertion Sort

Insertion Sort(Ain);   //Sorts A[1....n];

 

　　The graph is pseudocode，The whole idea of the pseudocode(伪代码) is to try to get the algorithms as short as possible,while still understanding what the individual steps are;
　　In practice, there actually have been languages that use indentation(缩进) as a mean of showing the nesting of thing. It's generally a bad idea, because if things go over one page to another, you cannot tell what level of nesting it is.
　　with nesting it's much easier to tell. But indentation is good for us(study algorithm). because it just keeps things short and makes fewer things to write down.

 

Let’s try to figure out(理解) a little bit what this does?
　　It basically takes an array A. We’re setting running the outer loop from j is 2 to n. And the inner loop is j minus 1. We are looking some element here j. And What we do essentially is we pull a value out here that we call the key. And the invariant(不变的) that start to key part of the array is sorted. And the goal each time through the loop is to increase is to add one to the length of the things that are sorted. We keep copying up untile we find the place where this key goes, and then we insert it in that place. That’s we call the insertion sort.

 

Give the Example:

 

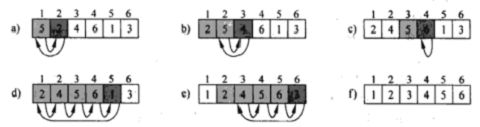
Let's take a look at the issue of running time?
1.The running time depends on a lot of things.
One thing it depends on is the input self
For example, if the input is already sorted...then insertion sort has very little work to do.
Question: whereas, what's the worst case for insertion sort?
Answer: if it's reverse sorted then it's going to have to do a lot of work..
because it's going to have shuffle everything over on each step of the outer loop. (在每一次循环里把元素都整理一遍)

2.The running time depends on input size
For example, if we six billion elements, It's going to take longer time than we have six elements .Typically, we are going to parameterize things in the input size

3.The last want to talk about, the upper bonds(上届) on the running time
the time is no more than a certain amount(总计). the reason is because that represents a guarantee to the user. for example, I tell you here's program and it won't run more than three seconds, that gives you real information about how you could use it. for example in a the real time setting
　　(most important: represent a guarantee to the user)

 

Kinds of analysis
1. T(n) = max time on any input of the size n
　　we define T of n, be the maximum time on any input of the size n...
　　for example we 're looking at the worst case of the insertion sort.  Because that the way we are going to make a guarantee to the users, How much time the algorithm use.
 

2. Average case
　　T(n) = expected time over all input of size n
　　Here T of n is then the expected time over all inputs of size n...

　　Question: So, What does that mean expected time?
　　Answer: It's the time of every input time the probability, It's a way of taking a weighted average
　　Question: So, How do I know What the probability of every input is?
　　Answer: need of assumption of the statistical distribution(分布) of inputs. For the common assumption that all inputs are equally likely. That's called the uniform distribution

3. Best case analysis
　　We call the best case analysis is bogus(假象) because The best case is a bogus because It doesn't really do much for us.

 

What's insertion sorts worst case time?
　　we are just talk BIG IDEA(大局观), we don't care a algorithm on different computers.

　　the idea is called asymptotic(渐近的) analysis...
　　1. Ignore the machine running time, we look at the growth of the running time. we adopt some notations(符号) that are going to help us.
 Θ-natation: from a formula, just drop low order terms and ignore leading constants.
　　
　　For example if I have a formula like: 3n^3 + 90n^2 - 50n + 6044
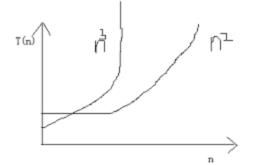
　　Because the n^3 bigger than n^2, so we drop the low-order terms.
　　So, 3n^3 + 90n^2 - 50n + 6044 = Θ(n^3)
　　So, n→∽, Θ(n^2) algorithm beats Θ(n^3), As the chart:

　　

 

(题外话）
　　we have to both balance our mathematical understanding and our enginner common sense(工程直觉) in order to do good programming. So, just done analysis of algorithm doesn't automatically make . a good programmer. understand when they are relevant and when they are not relevant(相关)
　　If you want to a good programmer, you just programmer every day two years, you will be an excellent programmer. If you want to be a world-class programmer, you can program every day for ten years. or you can program every day for two years and take an algorithms class. (laugh...)

 

Insertion sort analysis

 

 

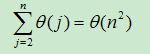
　　We assume is that every operation, every element operation is going to take some constant amount of time. But we don’t have to worry about what that constant is, because we’re going to be doing asymptotic(渐近) analysis.
　　So, we’re going to go through this loop, j is going from 2 to n, and then we’re going to add up the work that we do within the loop.

　　We can sort of write that in math as sum of j equals 2 to n. Such as :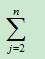 

　　Question: But in the inner loop, in the worst case, How many operations are going on here for each value of j?

　　Answer: We can say that is theta j work

　　

　　Tip: You have to be very careful because theta(Θ) is a week notation