R语言实现图像的边缘检测
文章目录
-
- 8 偏导数和边缘检测
-
- 基于偏导数的边缘检测
- Roberts算子
- 其他算子
8 偏导数和边缘检测
基于偏导数的边缘检测
灰度图像是天然的 z = f ( x , y ) z=f(x,y) z=f(x,y)函数,尽管以一种差分化的形式存在。其中, x , y x,y x,y分别代表图像坐标系中的坐标, z z z可以表示灰度图像的灰度值。
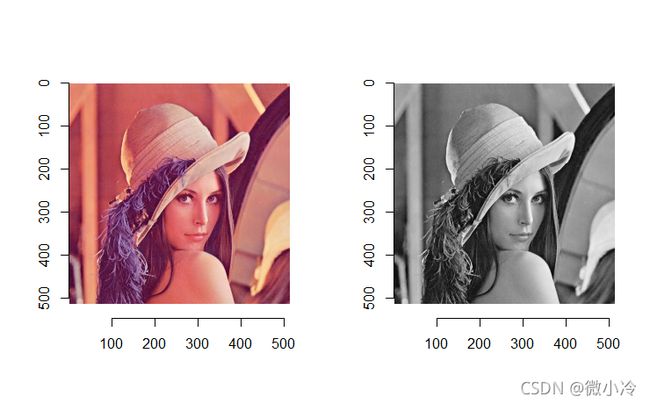
那么接下来我们可以观察一下偏导数作用在图像上是一个什么效果。图片当然是最经典的lena
library(imager)
img = load.image("lena.jpg")
dim(img)
[1] 512 512 1 3
gray = grayscale(img)
par(mfrow=c(1,2))
plot(img)
plot(gray)
gray显然变成了灰度图像,从其维度就能看得出来,然后将其变为二维的数组,接下来就可以进行求导操作了。
dim(gray)
[1] 512 512 1 1
mat = array(gray,dim=c(512,512))
mat_x = diff(mat,1)
mat_y = t(diff(t(mat),1))
par(mfrow=c(1,2))
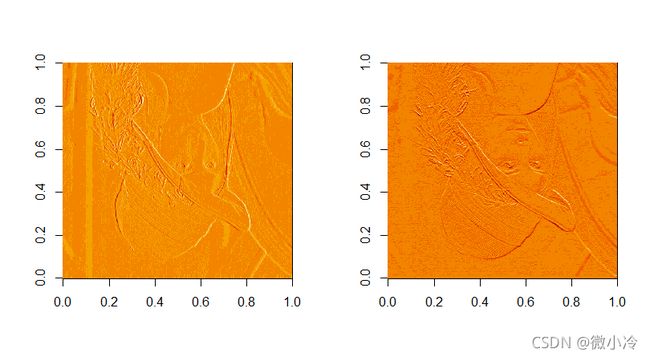
image(mat_x)
image(mat_y)
由于图像坐标系默认是从上向下为 y y y轴,从左向右为 x x x轴,所以在我们熟知的坐标系中,图像是上下颠倒的。而且R语言还非常智能(障)地添加了一层伪彩色,这让我们更加清晰地看出,对图像进行差分操作,提取出了边缘信息。
这很容易理解,所谓“边缘”,往往意味着变化较大的点,如果我们抽取lena图的任意一行,
a=mat[256,]
par(mfrow=c(1,2))
plot(a,type='l')
plot(diff(a,1),type='l')
在变化剧烈处,相应地导数较大。
若将偏导数在图像空间中展开,由于任意两个像素点之间的差恒为1,则可得到其差分形式
∂ u n , m ∂ x = u n + 1 , m − u n , m 1 \frac{\partial u_{n,m}}{\partial x}=\frac{u_{n+1,m}-u_{n,m}}{1} ∂x∂un,m=1un+1,m−un,m
由于这种差分方法利用了 n n n前面的值 n + 1 n+1 n+1,故谓之前向差分;相应地可有后向差分
∂ u n , m ∂ x = u n , m − u n − 1 , m 1 \frac{\partial u_{n,m}}{\partial x}=\frac{u_{n,m}-u_{n-1,m}}{1} ∂x∂un,m=1un,m−un−1,m
二者的均值,即中心差分
∂ u n , m ∂ x = u n + 1 , m − u n − 1 , m 2 \frac{\partial u_{n,m}}{\partial x}=\frac{u_{n+1,m}-u_{n-1,m}}{2} ∂x∂un,m=2un+1,m−un−1,m
Roberts算子
求导是对整个函数的定义域展开的一次性操作,但在考察其差分形式之后却发现,数值偏导数可以写成一种对局部区域的反复操作。
例如,就前向差分而言,可以对图像的任意一个子矩阵
[ u n m u n + 1 , m u n , m + 1 u n + 1 , m + 1 ] \begin{bmatrix} u_{nm}&u_{n+1,m}\\ u_{n,m+1}&u_{n+1,m+1} \end{bmatrix} [unmun,m+1un+1,mun+1,m+1]
进行一个简单的内积
u n ′ ( m n ) = [ u n m u n + 1 , m ] ⋅ [ − 1 1 ] u'_n(mn)=\begin{bmatrix} u_{nm}&u_{n+1,m} \end{bmatrix}\cdot\begin{bmatrix} -1&1 \end{bmatrix} un′(mn)=[unmun+1,m]⋅[−11]
其中, [ − 1 , 1 ] [-1,1] [−1,1]可以定义为梯度算子,表示的是对图像的 x x x方向的数值偏导数。
同理, [ − 1 , 1 ] T [-1,1]^T [−1,1]T为梯度算子的另一部分——对 y y y方向的数值偏导数。这两者在进行边缘检测时所展现出来的威力前文已经感受过了,但回顾方向导数的概念,无论 ∂ ∂ x \frac{\partial}{\partial x} ∂x∂还是 ∂ ∂ y \frac{\partial}{\partial y} ∂y∂,均只能表示单一方向的边缘。
如果将二者进行延拓,使之维数相等,则可分别写为
[ − 1 1 0 0 ] , [ − 1 0 1 0 ] \begin{bmatrix} -1&1\\0&0 \end{bmatrix}, \begin{bmatrix} -1&0\\1&0 \end{bmatrix} [−1010],[−1100]
二者的线性组合,是否能够代表其任意方向的边缘信息呢?
记
M ( θ ) = [ − 1 1 0 0 ] 2 cos θ + [ − 1 0 1 0 ] 2 sin θ M(\theta)= \begin{bmatrix} -1&1\\0&0 \end{bmatrix}\sqrt 2\cos\theta+ \begin{bmatrix} -1&0\\1&0 \end{bmatrix}\sqrt 2\sin\theta M(θ)=[−1010]2cosθ+[−1100]2sinθ
当 M ( θ ) M(\theta) M(θ)作用于图像时,可以表示为
U ∗ M ( θ ) = u x ′ cos θ + u y ′ sin θ U*M(\theta)=u'_x\cos\theta+u'_y\sin\theta U∗M(θ)=ux′cosθ+uy′sinθ
theta = c(pi/3,pi/4,pi/5,pi/6)
par(mfrow=c(2,2))
for(i in 1:4)
image(mat_x[,1:511]*cos(theta[i])+mat_y[1:511,]*sin(theta[i]))
可以看到,最后一张图片的法向角度为 30 ° 30° 30°,而其右下角正好有一个 30 ° 30° 30°附近的清晰的边缘。
当 θ = − π 4 \theta=-\frac{\pi}{4} θ=−4π时,
M ( θ ) = [ 0 1 − 1 0 ] M(\theta)=\begin{bmatrix} 0&1\\-1&0 \end{bmatrix} M(θ)=[0−110]
此即Roberts算子,代表的是 − π 4 -\frac{\pi}{4} −4π方向的边缘信息。
其他算子
如果通过中心差分来定义算子,则统一维度后,其 x x x和 y y y向的梯度算子分别写为
[ − 1 0 1 − 1 0 1 − 1 0 1 ] , [ − 1 − 1 − 1 0 0 0 1 1 1 ] \begin{bmatrix} -1&0&1\\-1&0&1\\-1&0&1\\ \end{bmatrix}, \begin{bmatrix} -1&-1&-1\\0&0&0\\1&1&1\\ \end{bmatrix} −1−1−1000111 , −101−101−101
此即Prewitt算子。
需要注意的是,这里所谓的“统一维度”,并非仅仅做了一个表面上的工作,实际上,每增加一个维度,都意味着增加一组计算。本来 u n m u_{nm} unm点沿着 x x x方向的导数和 m + 1 m+1 m+1行并没有关系,但由于Prewitt算子的介入,从而使得两者发生了关系。
Sobel算子为Prewitt增添了中心值的权重,记为
[ − 1 0 1 − 2 0 2 − 1 0 1 ] , [ − 1 − 2 − 1 0 0 0 1 2 1 ] \begin{bmatrix} -1&0&1\\-2&0&2\\-1&0&1\\ \end{bmatrix}, \begin{bmatrix} -1&-2&-1\\0&0&0\\1&2&1\\ \end{bmatrix} −1−2−1000121 , −101−202−101