可持久化数组-从入门到入土
什么是数组?
\(qwq\),这个问题就有点悬了~~。我们要明白数组是一个一维体,也是很多数据结构的基础。
什么是可持久化?
可持久化就是可以查询历史的类型的数据结构。就比如,我有一个数组,一共有\(n\)次操作,操作包括着插入和回到历史状态。
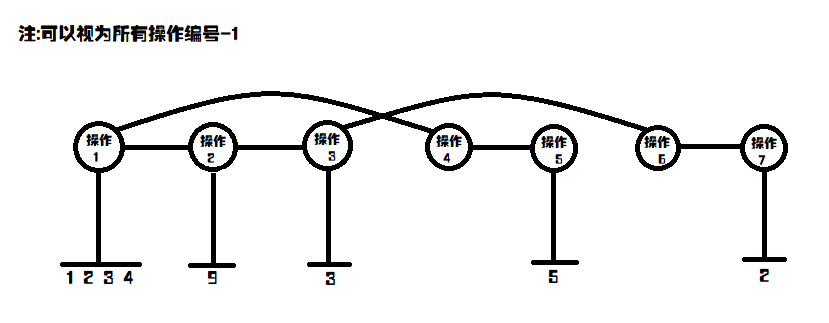
就是这样子的:
这就叫可持久化。不只是可持久化数组,还有可持久化线段树,可持久化并查集.....
最简单的方法
因为我们的数组是一维的,又要可持久化,我们就可以开一个二维数组来存储每一次操作的状态,就如上图。每一次插入,我们就新用一个数组\(num[i]=num[i-1]\),然后\(num[i,n+1]=\)插入的数。
我们可以探求一下复杂度。
\(I.\)编程复杂度:贼简单。
\(II.\)时间复杂度,\(m\)次操作。\(O(m)\)。(每一次操作达到\(O(1)\))
\(III.\)空间复杂度,\(O(n^2)\)。
好的,我们来看一下这道题目:高级打字机。
例题
它有\(3\)种操作:
\(I.T\ x\):在文章末尾打下一个小写字母\(x\)。(\(type\)操作)
\(II.U\ x\):撤销最后的\(x\)次修改操作。(\(Undo\)操作)
\(III.Q\ x\):询问当前文章中第\(x\)个字母并输出。(\(Query\)操作,
注意\(Query\)操作并不算修改操作)
然后让我们直奔高级挑战和IOI挑战。
<高级挑战>
对于200%的数据 n<=100000;Undo操作可以撤销Undo操作。
必须使用在线算法完成该题。 我们可以分析出,如果\(Undo\)到操作\(x\)以前,那么现在\(i\)到\(i-x+1\)的操作全部是不用做的(包括\(Undo\)本身)。那么我们就可以把这道题转化成可持久化数组的题目来做。可是我们看到数据:n<=100000,什么鬼?\(O(n^2)\)顶不住啊!(数据太水,\(90\)分)
寻找规律-找到合适的数据结构
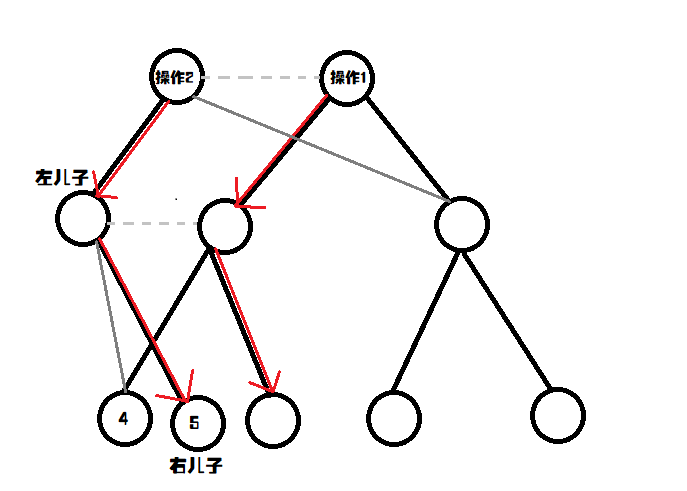
我们拿刚刚的例子:\(1\ 2\ 3\ 4\)。(现在要插入\(9\))
插入后原来的数组是不变的,所以\(1\ 2\ 3\ 4\ 9\)可以分为:\(1\ 2\ 3\ 4\)和\(9\)。这样子我们就可以节省很多空间!
如果是最后一个点为根,那么这就不是一棵树。但是如果以第一个点作为根,那么这就是一颗合法的树。这是可以证明的,因为操作只能往前面(祖宗)的操作连线,就成为了一个树边。而往祖宗连线了就无法和父亲连线,所以就不会出现图。
然后,我们就大功告成了!假如我们要查询操作\(7\)的数组是什么,我们就可以从\(7\)的父亲往上找,然后倒过来输出就可以了!!
这样子整个就变成了\(Trie\)。
分析复杂度
\(I.\)编程复杂度:一般般,类似于并查集,存储的是位置。(一开始的数组处理一下)
\(II.\)时间复杂度,每一次修改是\(O(1)\),只需要连边。但是!!查询的时间复杂度的极端情况是\(O(m)\)!!(综合起来就是\(O(m^2)\))
(你可能会问,这里是\(O(m)\),但是打字机那题也是\(O(m)\),它要查询第\(x\)个字母诶,假如\(x=1\)如何?那你就要找\(m\)次,你说是\(n\)次也无妨)
\(III.\)空间复杂度,\(O(n+m)\)。
极端情况
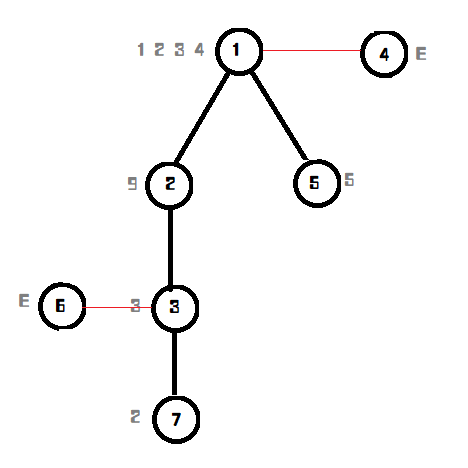
因为极端很严重,时间复杂度综合起来是\(O(n^2)\),\(100000^2\)。我们可以想到,则容易成为一个偏树。
首先,我们可以想到,如果一个点是"E"的话,我们可以直接无视它。查询它的时候直接把它的父亲输出就可以了。
到现在这种情况,打字机那题应该就\(AC\)了,根据数据来说很水,不可能全部都是插入操作,那么就是\(1/3n\),\((1/3n)^2\)大约是\(11108889\)。(我们已经成功的把历史操作无视掉了\(qwq\)!成功!\(qwq\))
降低时间复杂度
我们可以直接把时间复杂度降到\(O(1)\),而其空间(最差)将会变为\(O(n^2)\)。我们可以记录每一个操作的点的位置,每一个点就可以往上面所有的父亲都连线。这样子无疑连线的指针就会爆空间,大约是\(1/2(1/3n)(1/3n-1)=O(n)\)。如果\(n=100000\),那么空间就应该是\(5,5553,3333\),显然爆炸。当然如果\(n=1000000\),数据不强,就应该可以卡到\(O(n\ log\ n)\)的空间复杂度。
可持久化线段树
线段树维护数组
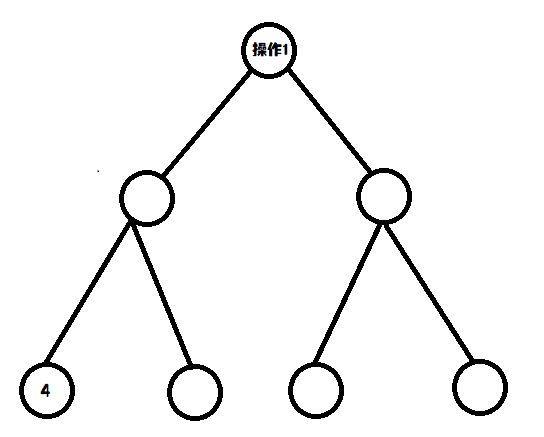
线段树就是比较基础的东西,我们可以将其看成维护数组的一个工具。那么怎么维护数组呢?我们视为叶子节点就是存储数组的地方,如下图:
要注意非叶子节点不存储任何东西!
我们为什么要存储在这样一个数据结构中呢?假如我们我要查询第\(3\)个数字,我们就可以直接往\(l=3,r=3\)的地方跑一跑,时间复杂度\(O(log\ n)\)。假如是可持久化数组,我们就可以开\(m\)个线段树,进行存储。
还需要注意的是我们的线段树的叶子节点要保持在\(m\)个,也可以开线段树数组的时候直接开大一点的数。
目的所在
我们不可能傻到这种时间复杂度\(O(m\ log\ n)\),空间复杂度\(O(m\ n\ log\ n)\)的数据结构去存储,我们的目的是将这些子节点独立化。怎么说?
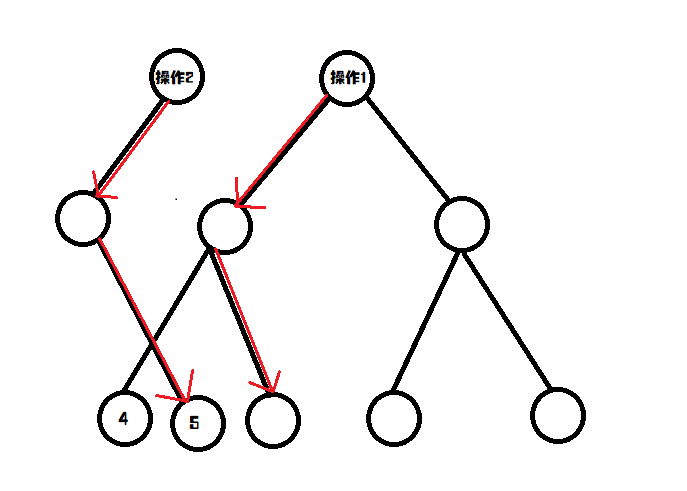
假如我们存储了这样子的线段树:(我们还要记录一下根的位置,这里我们运用动态开点。也就是我们需要一个点,开一个点,并且记录左右儿子(指针))
我们发现\(1\)是重复的,还有很多空间是浪费的,我们就可以这样子:
所以说,我们把叶子节点独立了,也只有父亲节点来连接它们。而每一次操作,我们只需要一条长度为\(log\ n\)的数链,每一个点都可以继承前一个操作没有改变的点。
而每一次插入一个点,我们找到上一次操作的根,然后从上往下找到这个数字应有的位置(一般是现在数组的数的个数\(+1\),也就是\(n+1\))。在找的同时,创建节点,如果某一个儿子不是我要前往的方向,就向这个儿子连边,方向不变。然后新建儿子节点,方向为刚刚连接的反方向。
模拟插入
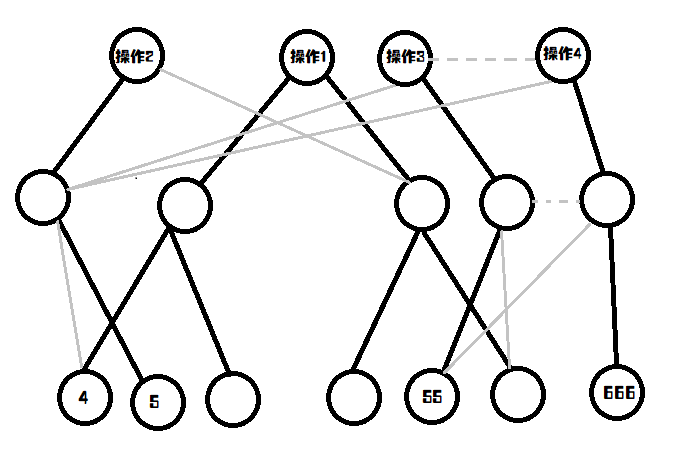
一共有4个操作:
操作1:插入5
操作2:插入4
操作3:插入55
操作4:插入666这样子我们就可以提取每一个操作的根节点,然后按照线段树的方法去查找,比如查找现在数组的第\(3\)个数字。我们就看一下现在操作的根节点在哪里,然后按照\(l=3,r=3\)往下找一找,就可以找到那个数字。
谈谈历史状态
其实我们可以记录一个数\(now\),是现在操作的根节点编号。如果要回到历史(比如回到\(x\)次操作以前),我们就可以\(root[now]:=root[now-x-1];\)。而查找的时候我们就可以从\(root[now]\)开始。每一次插入我们都是依附上一个\(root[now]\)来弄(包括\(root[now]\)回归过历史)。
分析复杂度
\(I.\)编程复杂度:一般般,类似于线段树。
\(II.\)时间复杂度:查询一次\(O(log\ n)\),插入一次\(O(log\ n)\),返回历史一次\(O(1)\)。
\(III.\)空间复杂度,\(O(n\ log\ n)\)。
锦囊
高级打字机可持久化线段树解法:传送门。
可持久化线段树
怎么可以让这可持久化线段树的节点全部用上呢?
主席树问题扩展包
区间\(num\)出现次数问题
给定一个区间\(l,r\),让你求区间有多少个数字等于\(num\)。
主席树多用于权值线段树,因为权值线段树满足减法原理。像这一道题目,我们记录的权值线段树代表的是一段区间\(1,i\)每一个数字的个数,就如:
数组: 1 2 1每一次一个数插入我们都要对其进行重建,存储。如果我们要查询\(2,3\)区间有多少个\(1\),我们就可以用叶子结点的编号为\(1\)的两条分别为\(root_{2-1}\),\(root_3\)的进行差分(也就等于区间\(1,3\)减去\(1,1\)得到\(2,3\))。最后就得到叶子结点为\(1\),出现次数为\(1\)。
区间最值问题
假如我们的叶子结点存的是权值,那么我们的任务就是看一下差分之后的最右边的存在的数字。当然我们也可以用下方的第\(K\)大来做,具体做法详见区间第\(K\)大。
区间第\(K\)大问题
这个问题就需要补习,如果您还不知道如何求第\(K\)大(权值线段树),请出门往右走。
一个区间,可以把它看作是这样子的:
我们用橙色的减去红色的,就得到了灰色的区间。没错,这就是前缀和。
在可持久化线段树中,每一个数字的读入看为一次插入。而查找区间\(l,r\)的时候我们就可以把以\(root[r]\) (代表区间\(1,r\))为的线段树 减去以\(root[l]\) (代表区间\(1,l\)) 为的线段树,减去指的是每一个节点的值减去。已经清楚权值线段树的同学都知道,减去了以后,数的出现就限制在那段区间,然后做一遍第\(K\)大。
锦囊
包括技巧,实现,讲解主席树和权值线段树求第\(K\)大:传送门。
区间不同数问题
\(N\)个数字,\(M\)次操作。每一次操作只有查询:给定一个区间\(l,r\),问你\(l,r\)有多少个数字不相同。
如果运用于离线,那么这道题就可以莫队甚至分块,当然也可以主席树。
我们考虑,如果一个数\(num_i\)的\(last_i\)(前一个与\(num_i\)相同的数)在\(l,r\)区间里面,那么\(num_i\)就是一个多余的数字。那么我们把问题转化为区间有多少个\(last_i>=l\)就可以了。这样子就可以套一套权值线段树,然后主席树。
HH的项链·锦囊
[题面
,
blog]
后记
用时:\(10\)天,每天\(0.1\)到\(5\)小时。(包括想新的东西,想原来的想法,想原来我在想什么原来的想法,发呆)
鸣谢:\(Myself\)。还有上方博客中鸣谢的大佬。
后记:本来想到了很多维护可持久化数组的方法,不过总是没有突破屏障。坚信,可持久化线段树固然巧妙,不过有太多节点变成了无用的,所以肯定有更好的方法来维护可持久化数组。这个留给大家思考。
以下是废用的草稿,允以借鉴:
\(I.\)https://i.loli.net/2018/08/04/5b657df82058e.png
\(II.\)https://i.loli.net/2018/08/04/5b657df9cd617.png
\(III.\)https://cdn.luogu.org/upload/pic/26640.png
\(IV.\)https://cdn.luogu.org/upload/pic/25945.png
如果有大佬有了新的想法,或者写得有误(包括\(Markdown\)和\(LaTeX\)),可以联系我(\(Luogu\)私信)。