SLAM基础——聊一聊信息矩阵
文章目录
- 前言
- 1 :book: 信息矩阵
-
- 1-1 :bookmark: 信息矩阵是什么?有什么作用?
- 1-2 :bookmark: 信息矩阵与Hessian矩阵的关系
-
- 1-2-1 Hessian矩阵和H矩阵的关系
- 1-2-2 Hessian或H矩阵和信息矩阵的关系
- 2 :book: 信息矩阵与最小二乘的关联
-
- 2-1 :bookmark: 先谈一谈常规的最小二乘
- 2-2 :bookmark: 包含信息矩阵的最小二乘
- 3 :book: 信息矩阵如何更新的?
-
- 3-1 :bookmark: 舒尔补介绍
- 3-2 :bookmark: 在滑窗中信息矩阵的更新(以及矩阵块的变化)
-
- 3-2-1 回顾附录A的结论
- 3-2-2 划窗过程中的信息矩阵变化
- 3-2-3 步骤详解
- 3-2-4 marg之后留下信息介绍(先验)
- 3-3 :bookmark: 滑窗带来的问题,以及信息矩阵的零空间变化
- 3-4 :bookmark: 滑窗问题的解决(FEJ)
- 0 :book: 参考资料
前言
本文主要谈哪些问题?本文主要以信息矩阵为核心,发散畅谈~
- 谈一谈信息矩阵的作用,以及与Hessian矩阵的关系与作用。
- 谈一谈舒尔补的边缘化原理与本质
- 在舒尔补下信息矩阵的更新,先验的定义与本质。
- 信息矩阵更新牵涉到的零空间问题,以及FEJ的引入~
(参考资料较多,吸取了知乎等大佬的回答,也包含一家之言,欢迎批评指正)
1 信息矩阵
1-1 信息矩阵是什么?有什么作用?
本小节参考: 信息矩阵在图优化slam里面的作用 表示感谢
信息矩阵是一个scalar 表达不确定性
e i ( x ) = e i ( x ) T Ω i e i ( x ) e_{i}(\mathbf{x})=\mathbf{e}_{i}(\mathbf{x})^{T} \mathbf{\Omega}_{i} \mathbf{e}_{i}(\mathbf{x}) ei(x)=ei(x)TΩiei(x)
Described by information matrix Ω \Omega Ω
Ω = Σ − 1 \Omega=\Sigma^{-1} Ω=Σ−1
and information vector ξ \xi ξ
ξ = Σ − 1 μ \xi=\Sigma^{-1} \mu ξ=Σ−1μ
那为什么需要信息矩阵呢?
x ∗ = argmin x F ( x ) − − − − − global error (scalar) = argmin x ∑ i e i ( x ) − − − − − squared error terms (scalar) = argmin x ∑ i e i T ( x ) Ω i e i ( x ) − − − error terms (vector) \begin{aligned} \mathbf{x}^{*} &=\underset{\mathrm{x}}{\operatorname{argmin}} F(\mathrm{x}) ----- \quad \text { global error (scalar) } \\ &=\underset{\mathrm{x}}{\operatorname{argmin}} \sum_{i} e_{i}(\mathrm{x}) ----- \text { squared error terms (scalar) } \\ &=\underset{\mathrm{x}}{\operatorname{argmin}} \sum_{i} \mathrm{e}_{i}^{T}(\mathrm{x}) \Omega_{i} \mathrm{e}_{i}(\mathrm{x}) --- \text {error terms (vector) } \end{aligned} x∗=xargminF(x)−−−−− global error (scalar) =xargmini∑ei(x)−−−−− squared error terms (scalar) =xargmini∑eiT(x)Ωiei(x)−−−error terms (vector)
系统可能有很多传感器,传感器精度越高,对应的information matrix里面的系数会很大(这里是越大越好,因为它是协方差矩阵的逆矩阵),系数越大代表权重越高,表达的信息越多,在优化的过程中就越会被重视。用一个形象的数学表达式表达就是:
const int INT_MAX=1e9;
argmin( INT_MAX*(x-3)^2+1/INT_MAX*(x-1)^2))
那么INT MAX就代表我们的精确传感器,那么优化的结果肯定是 x=3;也就是说,我们更加相信我们好的传感器
1-2 信息矩阵与Hessian矩阵的关系
本小节参考链接:
文章
[SLAM的滑动窗口算法中,在边缘化时,高斯牛顿法的信息矩阵为什么是 优化变量协方差的逆?][Why is the observed Fisher information defined as the Hessian of the log-likelihood?]
Maximum Likelihood Estimation (MLE).pdf
先放出结论:
Hessian矩阵在最大似然(MLE)问题中被认为约等于信息矩阵,所以一般也会将Hessian矩阵直接当做信息矩阵对待。
协方差的逆=信息矩阵,这个结论是建立在假设分布是高斯分布这个前提下,计算最大后验概率(MAP)优化问题得出来的
1-2-1 Hessian矩阵和H矩阵的关系
Hessian矩阵平时接触的可能不多, 但是Hessian矩阵的近似矩阵H矩阵就比较多了, 因为总是在求解优化问题,必不可少的就会接触到优化问题的H矩阵, 通常我们见到的都是最小二乘问题中的H矩 阵, 如下有:
E = ∥ z − f ( x ) ∥ w 2 = ∥ z − f ( x ) + J δ x ∥ w 2 = ( e + J δ x ) T W ( e + J δ x ) = e T w e + δ x T J T W e + e T W J δ x + δ x T J T W J δ x \begin{aligned} E &=\|z-f(x)\|_{w}^{2}=\|z-f(x)+J \delta x\|_{w}^{2} \\ &=(e+J \delta x)^{T} W(e+J \delta x) \\ &=e^{T} w e+\delta x^{T} J^{T} W e+e^{T} W J \delta x+\delta x^{T} J^{T} W J \delta x \end{aligned} E=∥z−f(x)∥w2=∥z−f(x)+Jδx∥w2=(e+Jδx)TW(e+Jδx)=eTwe+δxTJTWe+eTWJδx+δxTJTWJδx
其中 J T W J J^{T} W J JTWJ 就称为 H \mathrm{H} H 矩阵。
Hessian矩阵其实说白了就是 E E E 对于状态变量 x x x 的二阶偏导数。而H矩阵是对Hessian矩阵的近似, 主要是为了加速计算。
1-2-2 Hessian或H矩阵和信息矩阵的关系
结论:在最大似然估计问题中,Hessian矩阵通常被用来表示Information矩阵。(结论所参考的资料如下)
[Why is the observed Fisher information defined as the Hessian of the log-likelihood?]
注意:我们的最小二乘就是建立在最大似然估计的基础上的,这也是为什么在一些SLAM框架中,直接将Hessian矩阵当做了信息矩阵。而在最大似然估计中,就是将Hessian矩阵近似为了信息矩阵Maximum Likelihood Estimation (MLE).pdf
里面的公式(68),The Information matrix is the negative of the expectation of the Hessian.信息矩阵是Hessian期望的负值。
根据参考资料得出:
- 对于似然分布 p ( y ∣ x ) p(y|x) p(y∣x)而言,Information矩阵就是负对数似然问题的Hessian矩阵的期望;
- 对于分布 p ( x ) p(x) p(x)而言,负对数似然问题的协方差矩阵的逆就是Hessian矩阵;
VINS-mono应该就是采用这样的思路,直接将hessian矩阵作为了信息矩阵(information)(原因写在下面了)
问题:信息矩阵=协方差的逆,但是为什么有的还说Hessian矩阵在高斯牛顿中被近似认为是信息矩阵?哪一个是对的?
答:都对,信息矩阵就是协方差的逆,这个不是非线性优化推导出的,是假设分布是高斯分布,计算最大后验估计得到的一个优化问题。(参考后面信息矩阵与最小二乘的关系,就会发现推导过程中,假设分布属于高斯分布)
2 信息矩阵与最小二乘的关联
2-1 先谈一谈常规的最小二乘
残差函数 f ( x ) \mathbf{f}(\mathbf{x}) f(x) 为非线性函数,对其一阶泰勒近似有:
f ( x + Δ x ) ≈ ℓ ( Δ x ) ≡ f ( x ) + J Δ x \mathbf{f}(\mathbf{x}+\Delta \mathbf{x}) \approx \ell(\Delta \mathbf{x}) \equiv \mathbf{f}(\mathbf{x})+\mathbf{J} \Delta \mathbf{x} f(x+Δx)≈ℓ(Δx)≡f(x)+JΔx
请特别注意, 这里的 J \mathrm{J} J 是残差函数 f \mathrm{f} f 的雅克比矩阵。代入损失函数:
F ( x + Δ x ) ≈ L ( Δ x ) ≡ 1 2 ℓ ( Δ x ) ⊤ ℓ ( Δ x ) = 1 2 f ⊤ f + Δ x ⊤ J ⊤ f + 1 2 Δ x ⊤ J ⊤ J Δ x = F ( x ) + Δ x ⊤ J ⊤ f + 1 2 Δ x ⊤ J ⊤ J Δ x \begin{aligned} F(\mathbf{x}+\Delta \mathbf{x}) \approx L(\Delta \mathbf{x}) & \equiv \frac{1}{2} \ell(\Delta \mathbf{x})^{\top} \ell(\Delta \mathbf{x}) \\ &=\frac{1}{2} \mathbf{f}^{\top} \mathbf{f}+\Delta \mathbf{x}^{\top} \mathbf{J}^{\top} \mathbf{f}+\frac{1}{2} \Delta \mathbf{x}^{\top} \mathbf{J}^{\top} \mathbf{J} \Delta \mathbf{x} \\ &=F(\mathbf{x})+\Delta \mathbf{x}^{\top} \mathbf{J}^{\top} \mathbf{f}+\frac{1}{2} \Delta \mathbf{x}^{\top} \mathbf{J}^{\top} \mathbf{J} \Delta \mathbf{x} \end{aligned} F(x+Δx)≈L(Δx)≡21ℓ(Δx)⊤ℓ(Δx)=21f⊤f+Δx⊤J⊤f+21Δx⊤J⊤JΔx=F(x)+Δx⊤J⊤f+21Δx⊤J⊤JΔx
这样损失函数就近似成了一个二次函数,并且如果雅克比是满秩的, 则 J ⊤ J \mathbf{J}^{\top} \mathbf{J} J⊤J 正定,损失函数有最小值。
另外, 易得: F ′ ( x ) = ( J ⊤ f ) ⊤ F^{\prime}(\mathbf{x})=\left(\mathbf{J}^{\top} \mathbf{f}\right)^{\top} F′(x)=(J⊤f)⊤, 以及 F ′ ′ ( x ) ≈ J ⊤ J F^{\prime \prime}(\mathbf{x}) \approx \mathbf{J}^{\top} \mathbf{J} F′′(x)≈J⊤J.
2-2 包含信息矩阵的最小二乘
本小节主要回答下面问题:
有时候我们不写中间的协方差的逆,为什么??多出来的协方差的逆是怎么多出来的??
没有写那是假设其为1了。
SLAM问题建模
考虑某个状态 ξ \boldsymbol{\xi} ξ, 以及一次与该变量相关的观测 r i ∘ \mathbf{r}_{i \circ} ri∘ 由于噪声的存在, 观测服从概率分布 p ( r i ∣ ξ ) p\left(\mathbf{r}_{i} \mid \boldsymbol{\xi}\right) p(ri∣ξ) 。 多次观测时,各个测量值相互独立, 则多个测量相互独立,则多个测量 r = ( r 1 , … , r n ) ⊤ \mathbf{r}=\left(\mathbf{r}_{1}, \ldots, \mathbf{r}_{n}\right)^{\top} r=(r1,…,rn)⊤ 构建的似然概率为:
p ( r ∣ ξ ) = ∏ i p ( r i ∣ ξ ) p(\mathbf{r} \mid \boldsymbol{\xi})=\prod_{i} p\left(\mathbf{r}_{i} \mid \boldsymbol{\xi}\right) p(r∣ξ)=i∏p(ri∣ξ)
如果知道机器人状态的先验信息 p ( ξ ) p(\boldsymbol{\xi}) p(ξ), 如 GPS, 车轮码盘信息等, 则 根据 Bayes 法则,有后验概率:
p ( ξ ∣ r ) = p ( r ∣ ξ ) p ( ξ ) p ( r ) p(\boldsymbol{\xi} \mid \mathbf{r})=\frac{p(\mathbf{r} \mid \boldsymbol{\xi}) p(\boldsymbol{\xi})}{p(\mathbf{r})} p(ξ∣r)=p(r)p(r∣ξ)p(ξ)
通过最大后验估计,获得系统状态的最优估计:
ξ M A P = arg max ξ p ( ξ ∣ r ) \boldsymbol{\xi}_{\mathrm{MAP}}=\arg \max _{\xi} p(\boldsymbol{\xi} \mid \mathbf{r}) ξMAP=argξmaxp(ξ∣r)
后验公式中分母跟状态量无关,舍弃。最大后验变成了:
ξ M A P = arg max ξ ∏ i p ( r i ∣ ξ ) p ( ξ ) \boldsymbol{\xi}_{\mathrm{MAP}}=\arg \max _{\xi} \prod_{i} p\left(\mathbf{r}_{i} \mid \boldsymbol{\xi}\right) p(\boldsymbol{\xi}) ξMAP=argξmaxi∏p(ri∣ξ)p(ξ)
即
ξ M A P = arg min ξ [ − ∑ i log p ( r i ∣ ξ ) − log p ( ξ ) ] \boldsymbol{\xi}_{\mathrm{MAP}}=\arg \min _{\xi}\left[-\sum_{i} \log p\left(\mathbf{r}_{i} \mid \boldsymbol{\xi}\right)-\log p(\boldsymbol{\xi})\right] ξMAP=argξmin[−i∑logp(ri∣ξ)−logp(ξ)]
如果假设观测值服从多元高斯分布:
p ( r i ∣ ξ ) = N ( μ i , Σ i ) , p ( ξ ) = N ( μ ξ , Σ ξ ) p\left(\mathbf{r}_{i} \mid \boldsymbol{\xi}\right)=\mathcal{N}\left(\boldsymbol{\mu}_{i}, \boldsymbol{\Sigma}_{i}\right), p(\boldsymbol{\xi})=\mathcal{N}\left(\boldsymbol{\mu}_{\xi}, \boldsymbol{\Sigma}_{\xi}\right) p(ri∣ξ)=N(μi,Σi),p(ξ)=N(μξ,Σξ)
则有:
ξ M A P = argmin ξ ∑ i ∥ r i − μ i ∥ Σ i 2 + ∥ ξ − μ ξ ∥ Σ ξ 2 \boldsymbol{\xi}_{\mathrm{MAP}}=\underset{\boldsymbol{\xi}}{\operatorname{argmin}} \sum_{i}\left\|\mathbf{r}_{i}-\boldsymbol{\mu}_{i}\right\|_{\boldsymbol{\Sigma}_{i}}^{2}+\left\|\boldsymbol{\xi}-\boldsymbol{\mu}_{\xi}\right\|_{\Sigma_{\xi}}^{2} ξMAP=ξargmini∑∥ri−μi∥Σi2+∥∥ξ−μξ∥∥Σξ2
注意右下角的 ∥ . . ∥ Σ ξ 2 \|..\|_{\Sigma_{\xi}}^{2} ∥..∥Σξ2表示 ∥ . . ∥ 2 \|..\|_{}^{2} ∥..∥2需要除以 Σ ξ {\Sigma_{\xi}} Σξ,这也是为什么高斯牛顿中出现中间的协方差的逆的原因。不过有时候我们假设其为1了,也就是省略不写
这个最小二乘的求解为:(下面结果如何推导出的,看下面的细节说明)
J T Σ − 1 J δ ξ = − J T Σ − 1 r \mathbf{J}^{T} \mathbf{\Sigma}^{-1} \mathbf{J} \delta \boldsymbol{\xi}=-\mathbf{J}^{T} \mathbf{\Sigma}^{-1} \mathbf{r} JTΣ−1Jδξ=−JTΣ−1r
这里对上面省略掉的推到细节进行说明:
前期基础:
考虑一个任意的高维高斯分布 x ∼ N ( μ , Σ ) \boldsymbol{x} \sim N(\boldsymbol{\mu}, \mathbf{\Sigma}) x∼N(μ,Σ)它的概率密度函数展开形式为:
P ( x ) = 1 ( 2 π ) N det ( Σ ) exp ( − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) ) P(x)=\frac{1}{\sqrt{(2 \pi)^{N} \operatorname{det}(\mathbf{\Sigma})}} \exp \left(-\frac{1}{2}(x-\mu)^{T} \mathbf{\Sigma}^{-1}(x-\mu)\right) P(x)=(2π)Ndet(Σ)1exp(−21(x−μ)TΣ−1(x−μ))
取它的负对数, 则变为:
− ln ( P ( x ) ) = 1 2 ln ( ( 2 π ) N det ( Σ ) ) + 1 2 ( x − μ ) T Σ − 1 ( x − μ ) . -\ln (P(x))=\frac{1}{2} \ln \left((2 \pi)^{N} \operatorname{det}(\mathbf{\Sigma})\right)+\frac{1}{2}(x-\boldsymbol{\mu})^{T} \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu}) . −ln(P(x))=21ln((2π)Ndet(Σ))+21(x−μ)TΣ−1(x−μ).
对原分布求最大化相当于对负对数求最小化。在最小化上式的 x 时,第一项与 x 无关,可以略去。于是,只要最小化右侧的二次型项,就得到了对状态的最大似然估计。相当于在求:
x ∗ = arg min ( ( x − μ ) T Σ − 1 ( x − μ ) ) . \boldsymbol{x}^{*}=\arg \min \left((x-\boldsymbol{\mu})^{T} {\Sigma}^{-1}(x-\boldsymbol{\mu})\right) . x∗=argmin((x−μ)TΣ−1(x−μ)).
推导对于某一次观测:
z k , j = h ( y j , x k ) + v k , j z_{k, j}=h\left(y_{j}, x_{k}\right)+v_{k, j} zk,j=h(yj,xk)+vk,j
我们假设了噪声项 v k ∼ N ( 0 , Σ k , j ) \boldsymbol{v}_{k} \sim N\left(0, \boldsymbol{\Sigma}_{k, j}\right) vk∼N(0,Σk,j), 所以观测数据的条件概率为:
P ( z j , k ∣ x k , y j ) = N ( h ( y j , x k ) , Σ k , j ) . P\left(z_{j, k} \mid x_{k}, y_{j}\right)=N\left(h\left(y_{j}, x_{k}\right), {\Sigma}_{k, j}\right) . P(zj,k∣xk,yj)=N(h(yj,xk),Σk,j).
根据上面【前期基础】知识,我们相当于在求:
x ∗ = arg min ( ( z k , j − h ( x k , y j ) ) T Σ k , j − 1 ( z k , j − h ( x k , y j ) ) ) \boldsymbol{x}^{*}=\arg \min \left(\left(\boldsymbol{z}_{k, j}-h\left(\boldsymbol{x}_{k}, \boldsymbol{y}_{j}\right)\right)^{T} \boldsymbol{\Sigma}_{k, j}^{-1}\left(\boldsymbol{z}_{k, j}-h\left(\boldsymbol{x}_{k}, \boldsymbol{y}_{j}\right)\right)\right) x∗=argmin((zk,j−h(xk,yj))TΣk,j−1(zk,j−h(xk,yj)))
最终最小二乘F(x)为:
F ( x + Δ x ) = ∥ z − h ( x ) ∥ w 2 = ∥ z − h ( x ) + J δ x ∥ w 2 = ( e + J δ x ) T Σ − 1 ( e + J δ x ) = e T Σ − 1 e + 2 δ x T J T Σ − 1 e + δ x T J T Σ − 1 J δ x = F ( x ) + 2 δ x T J T Σ − 1 e + δ x T J T Σ − 1 J δ x \begin{aligned} F(x+\Delta {x}) &=\|z-h(x)\|_{w}^{2}=\|z-h(x)+J \delta x\|_{w}^{2} \\ &=(e+J \delta x)^{T} {\Sigma}^{-1}(e+J \delta x) \\ &=e^{T} {\Sigma}^{-1} e+2 \delta x^{T} J^{T} {\Sigma}^{-1} e+\delta x^{T} J^{T} {\Sigma}^{-1} J \delta x \\ &=F(x)+ 2\delta x^{T} J^{T} {\Sigma}^{-1} e+ \delta x^{T} J^{T} {\Sigma}^{-1} J \delta x \end{aligned} F(x+Δx)=∥z−h(x)∥w2=∥z−h(x)+Jδx∥w2=(e+Jδx)TΣ−1(e+Jδx)=eTΣ−1e+2δxTJTΣ−1e+δxTJTΣ−1Jδx=F(x)+2δxTJTΣ−1e+δxTJTΣ−1Jδx
根据解析求导,容易得出:
J T Σ − 1 J δ ξ = − J T Σ − 1 e \mathbf{J}^{T} \mathbf{\Sigma}^{-1} \mathbf{J} \delta \boldsymbol{\xi}=-\mathbf{J}^{T} \mathbf{\Sigma}^{-1} \mathbf{e} JTΣ−1Jδξ=−JTΣ−1e
3 信息矩阵如何更新的?
3-1 舒尔补介绍
参考我的博文
SLAM基础——舒尔补介绍
3-2 在滑窗中信息矩阵的更新(以及矩阵块的变化)
-
为什么 SLAM 需要滑动窗口算法?
- 随着 VSLAM 系统不断往新环境探索,就会有新的相机姿态以及看到新的环境特征,最小二乘残差就会越来越多,信息矩阵越来越大,计算量将不断增加。
- 为了保持优化变量的个数在一定范围内,需要使用滑动窗口算法动态增加或移除优化变量。
-
滑动窗口算法大致流程?
- 增加新的变量进入最小二乘系统优化
- 如果变量数目达到了一定的维度,则移除老的变量。
- SLAM 系统不断循环前面两步
-
怎么移除老的变量?直接丢弃这些变量吗?(参考下面几小结)
3-2-1 回顾附录A的结论
这里先拿出舒尔补里面的部分结论(在滑窗中计算的是边际概率的信息矩阵)
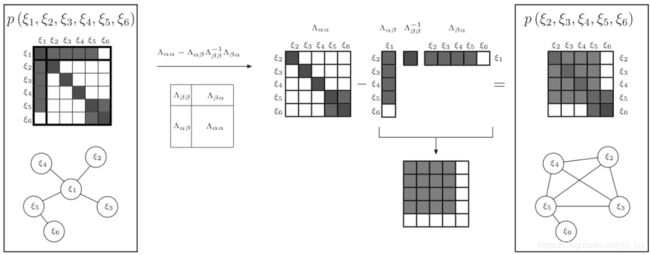
由舒尔补矩阵求逆公式可知,协方差矩阵各块和信息矩阵之间有:
[ A C ⊤ C D ] − 1 = [ A − 1 + A − 1 C ⊤ Δ A − 1 C A − 1 − A − 1 C ⊤ Δ A − 1 − Δ A − 1 C A − 1 Δ A − 1 ] ≜ [ Λ a a Λ a b Λ b a Λ b b ] \left[\begin{array}{cc} A & C^{\top} \\ C & D \end{array}\right]^{-1}=\left[\begin{array}{cc} A^{-1}+A^{-1} C^{\top} \Delta_{\mathrm{A}}^{-1} C A^{-1} & -A^{-1} C^{\top} \Delta_{\mathrm{A}}^{-1} \\ -\Delta_{\mathrm{A}}^{-1} C A^{-1} & \Delta_{\mathrm{A}}^{-1} \end{array}\right] \triangleq\left[\begin{array}{cc} \Lambda_{a a} & \Lambda_{a b} \\ \Lambda_{b a} & \Lambda_{b b} \end{array}\right] [ACC⊤D]−1=[A−1+A−1C⊤ΔA−1CA−1−ΔA−1CA−1−A−1C⊤ΔA−1ΔA−1]≜[ΛaaΛbaΛabΛbb]
由条件概率 P ( b ∣ a ) P(b \mid a) P(b∣a) 的协方差为 Δ A \Delta_{A} ΔA 以及公式, 易得其信息矩阵为
Δ A − 1 = Λ b b \Delta_{A}^{-1}=\Lambda_{b b} ΔA−1=Λbb
由边际概率 P ( a ) P(a) P(a) 的协方差为 A A A 以及公式 , 易得其信息矩阵为:
A − 1 = Λ a a − Λ a b Λ b b − 1 Λ b a A^{-1}=\Lambda_{a a}-\Lambda_{a b} \Lambda_{b b}^{-1} \Lambda_{b a} A−1=Λaa−ΛabΛbb−1Λba
或者:
D − 1 = Λ b b − Λ b a Λ a a − 1 Λ a b D^{-1}=\Lambda_{b b}-\Lambda_{b a} \Lambda_{a a}^{-1} \Lambda_{a b} D−1=Λbb−ΛbaΛaa−1Λab
这里的 A − 1 A^{-1} A−1或者 D − 1 D^{-1} D−1就是在下一次优化会使用的先验信息矩阵(又名:边际概率的信息矩阵)。
3-2-2 划窗过程中的信息矩阵变化
使用边际概率移除变量 ξ 1 \xi_{1} ξ1, 信息矩阵的变化过程如下
注意这里的矩阵要保留的是右下角
思考:如果是直接丢弃,信息矩阵如何变化?用边际概率来操作又会带来什么问题?
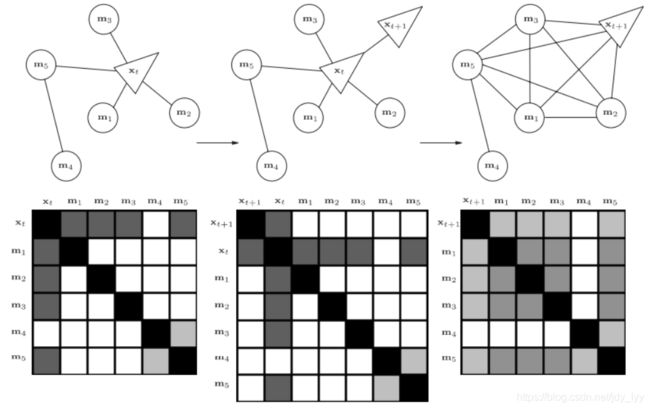
如下图优化系统中,随着 x t + 1 x_{t+1} xt+1 的进入,变量 x t x_{t} xt 被移除
3-2-3 步骤详解
总体流程是:先移除旧的变量,再加入新变量
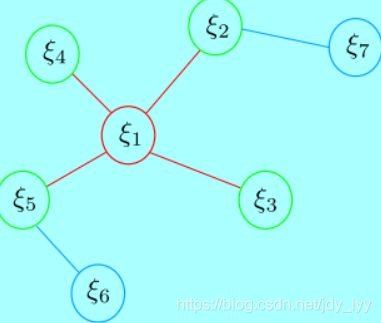
最开始的状态:
- 红色为被 marg 变量以及测量约束。
- 绿色为跟 marg 变量有关的保留变量。
- 蓝色为和 marg 变量无关联的变量。
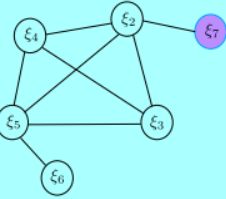
marg老变量之后的状态:
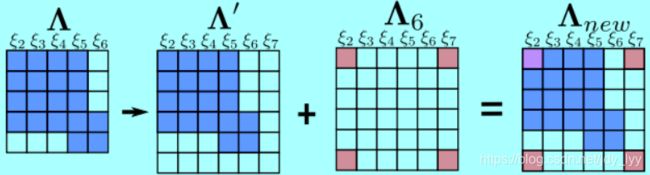
- STEP 1 新的变量 ξ 7 \xi_{7} ξ7跟老的变量 ξ 2 \xi_{2} ξ2之间存在观测信息,能构建残差 r 27 \mathbf{r}_{27} r27。
- STEP 2 新的残差加上之前marg留下的信息,构建新的最小二乘系统,对应的信息矩阵变化如下图所示
注意:
这里的 ξ 2 \xi_{2} ξ2自身的信息矩阵由两部分组成(与 ξ 1 \xi_{1} ξ1有关并在marg之后形成的,第二部分是新添加观测后形成的),这会使得系统存在潜在风险。
这两部分计算雅克比时的线性化点不同。这可能会导致信息矩阵的零空间发生变化,从而在求解时引入错误信息。
步骤总结:
-
(1) 在 t ∈ [ 0 , k ] s t \in[0, k] \mathrm{s} t∈[0,k]s 时刻, 系统中状态 量为 ξ i , i ∈ [ 1 , 6 ] \xi_{i}, i \in[1,6] ξi,i∈[1,6] 。第 k ′ k^{\prime} k′ 时刻,加入新的观 测和状态量 ξ 7 \xi_{7} ξ7
-
(2) 在第 k \mathrm{k} k 时刻,最小二乘优化完以后, marg 掉变量 ξ 1 ∘ \xi_{1 \circ} ξ1∘ 被 marg \operatorname{marg} marg 的状态量记为 x m \mathbf{x}_{m} xm, 剩余 的变量 ξ i , i ∈ [ 2 , 5 ] \xi_{i}, i \in[2,5] ξi,i∈[2,5] 记为 x r \mathbf{x}_{r} xr.
-
(3) marg 发生以后, x m \mathbf{x}_{m} xm 所有的变量以及对应的 测量将被丟弃。同时,这部分信息通过 marg \operatorname{marg} marg 操作传递给了保留变量 x r \mathrm{x}_{r} xr。 marg 变量的信息跟 ξ 6 \xi_{6} ξ6 不相关。
-
(4) 第 k ′ k^{\prime} k′ 时刻,加入新的状态量 ξ 7 ( \xi_{7}\left(\right. ξ7( 记作 x n \mathbf{x}_{n} xn ) 以 及对应的观测,开始新一轮最小二乘优化。
谈一谈新测量信息和旧测量信息构建新的系统的细节
在 k ′ k^{\prime} k′ 时刻, 新残差 r 27 \mathbf{r}_{27} r27 和先验信息 b p ( k ) , Λ p ( k ) \mathbf{b}_{p}(k), \boldsymbol{\Lambda}_{p}(k) bp(k),Λp(k) 以及残差 r 56 \mathbf{r}_{56} r56 构建新的最小二乘问题:
b ( k ′ ) = Π ⊤ b p ( k ) − ∑ ( i , j ) ∈ S a ( k ′ ) J i j ⊤ ( k ′ ) Σ i j − 1 r i j ( k ′ ) Λ ( k ′ ) = Π ⊤ Λ p ( k ) Π + ∑ ( i , j ) ∈ S a ( k ′ ) J i j ⊤ ( k ′ ) Σ i j − 1 J i j ( k ′ ) \begin{array}{c} \mathbf{b}\left(k^{\prime}\right)=\mathbf{\Pi}^{\top} \mathbf{b}_{p}(k)- \sum_{(i, j) \in \mathcal{S}_{a}\left(k^{\prime}\right)} \mathbf{J}_{i j}^{\top}\left(k^{\prime}\right) \boldsymbol{\Sigma}_{i j}^{-1} \mathbf{r}_{i j}\left(k^{\prime}\right) \\ \mathbf{\Lambda}\left(k^{\prime}\right)=\boldsymbol{\Pi}^{\top} \boldsymbol{\Lambda}_{p}(k) \mathbf{\Pi}+\sum_{(i, j) \in \mathcal{S}_{a}\left(k^{\prime}\right)} \mathbf{J}_{i j}^{\top}\left(k^{\prime}\right) \boldsymbol{\Sigma}_{i j}^{-1} \mathbf{J}_{i j}\left(k^{\prime}\right) \end{array} b(k′)=Π⊤bp(k)−∑(i,j)∈Sa(k′)Jij⊤(k′)Σij−1rij(k′)Λ(k′)=Π⊤Λp(k)Π+∑(i,j)∈Sa(k′)Jij⊤(k′)Σij−1Jij(k′)
- Π = [ I dim x r 0 ] \boldsymbol{\Pi}=\left[\begin{array}{ll}\mathbf{I}_{\operatorname{dim}} \mathbf{x}_{r} & \mathbf{0}\end{array}\right] Π=[Idimxr0] :用来将矩阵的维度进行扩张。
- S a \mathcal{S}_{a} Sa:用来表示除被marg 掉的测量以外的其他测量,如 r 56 , r 27 r_{56}, r_{27} r56,r27。
其他
说一说关于先验理解的一家之言:
并不能简简单单的理解为把新的信息矩阵传递到下一帧作为先验约束。从更深层面理解,是相互之间的约束关系变了,新的信息矩阵在图的表示上改变了,也就是说新的信息矩阵表达着一种新的图的关系(如上面图最后两个信息矩阵关系图的变化),这种新的关系是把本来不相关的两个变量关联起来了,这种新的关联,就是所谓的先验约束(一家之言)
3-2-4 marg之后留下信息介绍(先验)
变量命名声明
- x r \mathrm{x}_{r} xr:marg之后的保留变量
- x m \mathbf{x}_{m} xm:被 marg \operatorname{marg} marg 的变量
marg 前,变量 x m \mathbf{x}_{m} xm 以及对应测量 S m \mathcal{S}_{m} Sm 构建的最小二乘信息矩阵为:
b m ( k ) = [ b m m ( k ) b m r ( k ) ] = − ∑ ( i , j ) ∈ S m J i j ⊤ ( k ) Σ i j − 1 r i j Λ m ( k ) = [ Λ m m ( k ) Λ m r ( k ) Λ r m ( k ) Λ r r ( k ) ] = ∑ ( i , j ) ∈ S m J i j ⊤ ( k ) Σ i j − 1 J i j ( k ) \begin{aligned} \mathbf{b}_{m}(k) &=\left[\begin{array}{c} \mathbf{b}_{m m}(k) \\ \mathbf{b}_{m r}(k) \end{array}\right]=-\sum_{(i, j) \in \mathcal{S}_{m}} \mathbf{J}_{i j}^{\top}(k) \boldsymbol{\Sigma}_{i j}^{-1} \mathbf{r}_{i j} \\ \boldsymbol{\Lambda}_{m}(k) &=\left[\begin{array}{cc} \mathbf{\Lambda}_{m m}(k) & \boldsymbol{\Lambda}_{m r}(k) \\ \boldsymbol{\Lambda}_{r m}(k) & \boldsymbol{\Lambda}_{r r}(k) \end{array}\right]=\sum_{(i, j) \in \mathcal{S}_{m}} \mathbf{J}_{i j}^{\top}(k) \boldsymbol{\Sigma}_{i j}^{-1} \mathbf{J}_{i j}(k) \end{aligned} bm(k)Λm(k)=[bmm(k)bmr(k)]=−(i,j)∈Sm∑Jij⊤(k)Σij−1rij=[Λmm(k)Λrm(k)Λmr(k)Λrr(k)]=(i,j)∈Sm∑Jij⊤(k)Σij−1Jij(k)
marg 后, 变量 x m \mathbf{x}_{m} xm 的测量信息传递给了变量 x r \mathbf{x}_{r} xr :
b p ( k ) = b m r ( k ) − Λ r m ( k ) Λ m m − 1 ( k ) b m m ( k ) \mathbf{b}_{p}(k)=\mathbf{b}_{m r}(k)-\mathbf{\Lambda}_{r m}(k) \mathbf{\Lambda}_{m m}^{-1}(k) \mathbf{b}_{m m}(k) bp(k)=bmr(k)−Λrm(k)Λmm−1(k)bmm(k)
Λ p ( k ) = Λ r r ( k ) − Λ r m ( k ) Λ m m − 1 ( k ) Λ m r ( k ) \boldsymbol{\Lambda}_{p}(k)=\boldsymbol{\Lambda}_{r r}(k)-\boldsymbol{\Lambda}_{r m}(k) \boldsymbol{\Lambda}_{m m}^{-1}(k) \boldsymbol{\Lambda}_{m r}(k) Λp(k)=Λrr(k)−Λrm(k)Λmm−1(k)Λmr(k)
下标 p p p 表示 prior. 即这些信息将构建一个关于 x r \mathrm{x}_{r} xr 的先验信息。
谈一谈先验
我们可以从 b p ( k ) , Λ p ( k ) \mathbf{b}_{p}(k), \boldsymbol{\Lambda}_{p}(k) bp(k),Λp(k) 中反解出一个残差 r p ( k ) \mathbf{r}_{p}(k) rp(k) 和对应的雅克比矩 阵 J p ( k ) \mathbf{J}_{p}(k) Jp(k). 需要注意的是,随着变量 x r ( k ) \mathbf{x}_{r}(k) xr(k) 的后续不断优化变化, 残差 r p ( k ) \mathbf{r}_{p}(k) rp(k) 或者 b p ( k ) \mathbf{b}_{p}(k) bp(k) 也将跟着变化, 但雅克比 J p ( k ) \mathbf{J}_{p}(k) Jp(k) 则固定不变了。
说一说关于先验理解的一家之言:
并不能简简单单的理解为把新的信息矩阵传递到下一帧作为先验约束。从更深层面理解,是相互之间的约束关系变了,新的信息矩阵在图的表示上改变了,也就是说新的信息矩阵表达着一种新的图的关系(如上面图最后两个信息矩阵关系图的变化),这种新的关系是把本来不相关的两个变量关联起来了,这种新的关联,就是所谓的先验约束(一家之言)
3-3 滑窗带来的问题,以及信息矩阵的零空间变化
回顾上节
谈一谈新测量信息和旧测量信息构建新的系统的细节
在 k ′ k^{\prime} k′ 时刻, 新残差 r 27 \mathbf{r}_{27} r27 和先验信息 b p ( k ) , Λ p ( k ) \mathbf{b}_{p}(k), \boldsymbol{\Lambda}_{p}(k) bp(k),Λp(k) 以及残差 r 56 \mathbf{r}_{56} r56 构建新的最小二乘问题:
b ( k ′ ) = Π ⊤ b p ( k ) − ∑ ( i , j ) ∈ S a ( k ′ ) J i j ⊤ ( k ′ ) Σ i j − 1 r i j ( k ′ ) Λ ( k ′ ) = Π ⊤ Λ p ( k ) Π + ∑ ( i , j ) ∈ S a ( k ′ ) J i j ⊤ ( k ′ ) Σ i j − 1 J i j ( k ′ ) \begin{array}{c} \mathbf{b}\left(k^{\prime}\right)=\mathbf{\Pi}^{\top} \mathbf{b}_{p}(k)- \sum_{(i, j) \in \mathcal{S}_{a}\left(k^{\prime}\right)} \mathbf{J}_{i j}^{\top}\left(k^{\prime}\right) \boldsymbol{\Sigma}_{i j}^{-1} \mathbf{r}_{i j}\left(k^{\prime}\right) \\ \mathbf{\Lambda}\left(k^{\prime}\right)=\boldsymbol{\Pi}^{\top} \boldsymbol{\Lambda}_{p}(k) \mathbf{\Pi}+\sum_{(i, j) \in \mathcal{S}_{a}\left(k^{\prime}\right)} \mathbf{J}_{i j}^{\top}\left(k^{\prime}\right) \boldsymbol{\Sigma}_{i j}^{-1} \mathbf{J}_{i j}\left(k^{\prime}\right) \end{array} b(k′)=Π⊤bp(k)−∑(i,j)∈Sa(k′)Jij⊤(k′)Σij−1rij(k′)Λ(k′)=Π⊤Λp(k)Π+∑(i,j)∈Sa(k′)Jij⊤(k′)Σij−1Jij(k′)
- Π = [ I dim x r 0 ] \boldsymbol{\Pi}=\left[\begin{array}{ll}\mathbf{I}_{\operatorname{dim}} \mathbf{x}_{r} & \mathbf{0}\end{array}\right] Π=[Idimxr0] :用来将矩阵的维度进行扩张。
- S a \mathcal{S}_{a} Sa:用来表示除被marg 掉的测量以外的其他测量,如 r 56 , r 27 r_{56}, r_{27} r56,r27。
出现的问题
- 由于被 marg \operatorname{marg} marg 的变量以及对应的测量已被丢弃, 先验信息 Λ p ( k ) \boldsymbol{\Lambda}_{p}(k) Λp(k) 中关于 x r \mathrm{x}_{r} xr 的雅克比在后续求解中没法更新。
- 但 x r \mathbf{x}_{r} xr 中的部分变量还跟其他残差有联系, 如 ξ 2 , ξ 5 \xi_{2}, \xi_{5} ξ2,ξ5 。 这些残差如 r 27 \mathbf{r}_{27} r27 对 ξ 2 \xi_{2} ξ2 的雅克比会随着 ξ 2 \xi_{2} ξ2 的迭代更新而不断在最新的线性化 点处计算。
滑动窗口算法优化的时候,信息矩阵如上述公式变成了两部分,且这两部分计算雅克比时的线性化点不同。这可能会导致信息矩阵的零空间发生变化,从而在求解时引入错误信息。
比如: 求解单目 SLAM 进行 Bundle Adjustment 优化时,问题对应的 信息矩阵 Λ \mathbf{\Lambda} Λ 不满秩,对应的零空间为 N \mathbf{N} N, 用高斯牛顿求解时有
Λ δ x = b Λ δ x + N δ x = b \begin{aligned} \boldsymbol{\Lambda} \delta \mathbf{x} &=\mathbf{b} \\ \boldsymbol{\Lambda} \delta \mathbf{x}+\mathbf{N} \delta \mathbf{x} &=\mathbf{b} \end{aligned} ΛδxΛδx+Nδx=b=b
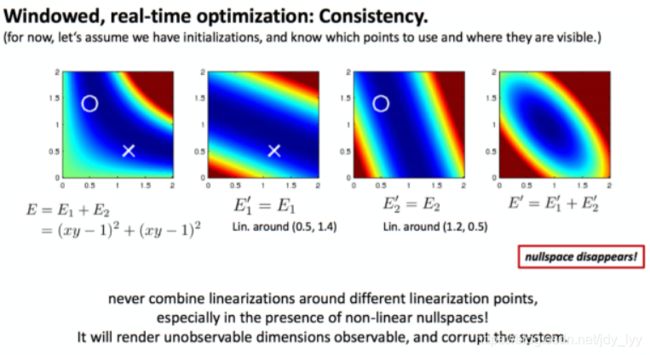
增量 δ x \delta x δx 在零空间维度下变化,并不会改变残差。这意味着系统可以有多个满足最小化损失函数的解 x ∘ \mathbf{x}_{\circ} x∘如下图所示,多个解的问题,变成了一个确定的解。不可观的量,变成了可观的。
我们的观测不是一下子全部到齐的,有着先后顺序的,在第一个观测到达的时候我们在(0.5,1.4)周围进行雅可比求解析如图2的 E 1 ′ {E}_{1}^{\prime} E1′,第二个观测再来的时候我们这次是在(1.2,0.5)周围求解雅可比如图3的 E 2 ′ {E}_{2}^{\prime} E2′,将新的和老的观测求解合并成图4.对比图4和图1,不可观的问题变得可观了。
3-4 滑窗问题的解决(FEJ)
滑动窗口中的问题
滑动窗口算法中,对于同一个变量,不同残差对其计算雅克比矩阵时线性化点可能不一致,导致信息矩阵可以分成两部分,相当于在信息矩阵中多加了一些信息,使得其零空间出现了变化
解决办法: First Estimated Jacobian
FEJ 算法:不同残差对同一个状态求雅克比时,线性化点必须一致。这样就能避免零空间退化而使得不可观变量变得可观。
比如: 计算 r 27 \mathbf{r}_{27} r27 对 ξ 2 \xi_{2} ξ2 的雅克比时, ξ 2 \xi_{2} ξ2 的线性话点必须和 r 12 \mathbf{r}_{12} r12 对其求导时一致。
所谓线性化点一致,也就是新老观测在求导的时候,求导变量数值不变(即使新观测来的时候,求导变量被优化了,也要使用变量优化之前的值求解雅可比)。
在边缘化的时候,FEJ的表现就是,一旦完成了marg,那么旧的雅可比矩阵就被固定住了,不能再变了。至于新来的观测残差球星求导雅可比就无所谓了。(简言之,同意误差对同一变量的雅可比求导必须保证线性化点一致。不能误差,或者不同变量之间没有要求线性化点必须一致。)
0 参考资料
信息矩阵在图优化slam里面的作用 【推荐】
OrbSLAM的Optimizer函数用到的信息矩阵如何理解?
SLAM的滑动窗口算法中,在边缘化时,高斯牛顿法的信息矩阵为什么是 优化变量协方差的逆?
[Why is the observed Fisher information defined as the Hessian of the log-likelihood?]
Maximum Likelihood Estimation (MLE).pdf
公式(68),
The Information matrix is the negative of the expectation of the Hessian.信息矩阵是Hessian期望的负值。
深蓝学院–手写vio课程
《视觉SLAM14讲》