《动手学深度学习》笔记

相关笔记

李沐的《动手学深度学习v2》 PyTorch版

---

前言

相关笔记随笔

04 数据预处理

chapter_preliminaries / pandas
使用pandas预处理原始数据，并将原始数据转换为张量格式

import os

os.makedirs(os.path.join('..', 'data'), exist_ok=True)
data_file = os.path.join('..', 'data', 'house_tiny.csv')
with open(data_file, 'w') as f:
    
    f.write('NumRooms,Alley,Price\n')  # 列名
    f.write('NA,Pave,127500\n')  # 每行表示一个数据样本
    f.write('2,NA,106000\n')
    f.write('4,NA,178100\n')
    f.write('NA,NA,140000\n')

不理解os.path.join()的作用

05 线性代数

chapter_preliminaries / linear-algerbra

基础概念

1. 标量 scalar

用只有一个元素的张量 tensor表示
tensor（3.）

2. 向量

1. 概念
   可以将其视为标量组成的列表，并且将这些标量值称为向量的元素或分量
   用一维张量处理向量
   tensor( [ 0 , 1 , 2 , 3 ] )
2. 定义
   x = torch.arange(4)
   x
   tensor( [ 0 , 1 , 2 , 3 ] )
3. 长度
   len（x）
   4
   向量或轴的维度：向量或轴的长度
   张量的维度：张量具有的轴数
   x.shape
   torch.Size( [ 4 ] )
   形状（shape）是一个元素组，列出了张量沿每个轴的长度
   对于只有一个轴的张量，形状只有一个元素

3. 矩阵

1. 定义
   A = torch.arange(16).reshape(16, 4)
   A
   tensor([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11], [12, 13, 14, 15]])
2. 转置
   A.T
   tensor([[ 0, 4, 8, 12], [ 1, 5, 9, 13], [ 2, 6, 10, 14], [ 3, 7, 11, 15]])
   A == A.T
   tensor([[ True, False, False, False], [False, True, False, False], [False, False, True, False], [False, False, False, True]])

4. 张量

1. 定义
   X = torch.arange(24).reshape(2, 3, 4)
   X
   tensor([[[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]], [[12, 13, 14, 15], [16, 17, 18, 19], [20, 21, 22, 23]]])
2. 算法的基本性质
   给定具有相同形状的任意两个张量，任何按元素二元运算的结果都将是相同形状的张量
   A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
   B = A.clone() # 通过分配新内存，将A的一个副本分配给B
   A, A + B, A * B # 两个矩阵的按元素乘法称为Hadamard积（Hadamard product）（数学符号 ⊙ ）
   将张量乘以或加上一个标量不会改变张量的形状，其中张量的每个元素都将与标量相加或相乘

5. 降维

randn函数——torch内置函数

help(torch.randn)
"""
Help on built-in function randn:

randn(...)
    randn(*size, *, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False) -> Tensor
    
    Returns a tensor filled with random numbers from a normal distribution
    with mean `0` and variance `1` (also called the standard normal
    distribution).
    
    .. math::
        \text{out}_{i} \sim \mathcal{N}(0, 1)
    
    The shape of the tensor is defined by the variable argument :attr:`size`.
    
    Args:
        size (int...): a sequence of integers defining the shape of the output tensor.
            Can be a variable number of arguments or a collection like a list or tuple.
    
    Keyword args:
        generator (:class:`torch.Generator`, optional): a pseudorandom number generator for sampling
        out (Tensor, optional): the output tensor.
        dtype (:class:`torch.dtype`, optional): the desired data type of returned tensor.
            Default: if ``None``, uses a global default (see :func:`torch.set_default_tensor_type`).
        layout (:class:`torch.layout`, optional): the desired layout of returned Tensor.
            Default: ``torch.strided``.
        device (:class:`torch.device`, optional): the desired device of returned tensor.
            Default: if ``None``, uses the current device for the default tensor type
            (see :func:`torch.set_default_tensor_type`). :attr:`device` will be the CPU
            for CPU tensor types and the current CUDA device for CUDA tensor types.
        requires_grad (bool, optional): If autograd should record operations on the
            returned tensor. Default: ``False``.
    
    Example::
    
        >>> torch.randn(4)
        tensor([-2.1436,  0.9966,  2.3426, -0.6366])
        >>> torch.randn(2, 3)
        tensor([[ 1.5954,  2.8929, -1.0923],
                [ 1.1719, -0.4709, -0.1996]])
"""
A = torch.randn(3, 4)
a = torch.randn(size=())

练习1：证明一个矩阵的转置的转置是，即 (⊤)⊤=

A = torch.randn(3, 4)
AT = A.T
ATT = AT.T
A, AT, ATT

练习2：给出两个矩阵 和 ，证明“它们转置的和”等于“它们和的转置”，即 ⊤+⊤=(+)⊤ 。

A, B = torch.randn(3, 4), torch.randn(3, 4)
AT, BT = A.T, B.T
AB, ATBT = A + B , AT + BT
AB, ATBT

练习3：给定任意方阵 ， +⊤ 总是对称的吗?为什么?

不会
大佬答案：

练习4：形状 (2,3,4) 的张量X。len(X)的输出结果是什么？

X = torch.arange(24).reshape(2, 3, 4)
len(X)
2

练习5：对于任意形状的张量X,len(X)是否总是对应于X特定轴的长度?这个轴是什么?

import torch
x, y, z = torch.arange(24).reshape(2,3,4), torch.arange(12).reshape(3,4), torch.arange(4)
len(x),len(y),len(z)
# (2, 3, 4)

对应axis=0这个轴

练习6：运行A/A.sum(axis=1)，看看会发生什么。你能分析原因吗？

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
A,A.sum(axis = 1),A.sum(axis=0),A.sum(axis = 1, keepdim = True)
"""
(tensor([[ 0.,  1.,  2.,  3.],
         [ 4.,  5.,  6.,  7.],
         [ 8.,  9., 10., 11.],
         [12., 13., 14., 15.],
         [16., 17., 18., 19.]]),
 tensor([ 6., 22., 38., 54., 70.]),
 tensor([40., 45., 50., 55.]),
 tensor([[ 6.],
         [22.],
         [38.],
         [54.],
         [70.]]))
"""

结果是报错：
RuntimeError: The size of tensor a (4) must match the size of tensor b (5) at non-singleton dimension 1
原因是：sum（axis = 1）会压缩张量维度，将此处的54的二维矩阵压缩（坍缩）为15的一维矩阵（行向量），
而sum（axis = 1， keepdim = True）则会保存axis = 1的维度，将A矩阵压缩为5*1的一维矩阵（列向量）

练习7：考虑一个具有形状 (2,3,4) 的张量，在轴0、1、2上的求和输出是什么形状?

[3,4], [2,4], [2,3]
copy大佬的解释：

练习8：为linalg.norm函数提供3个或更多轴的张量，并观察其输出。对于任意形状的张量这个函数计算得到什么?

8理解
大佬的答案：

06 矩阵计算

课程概念

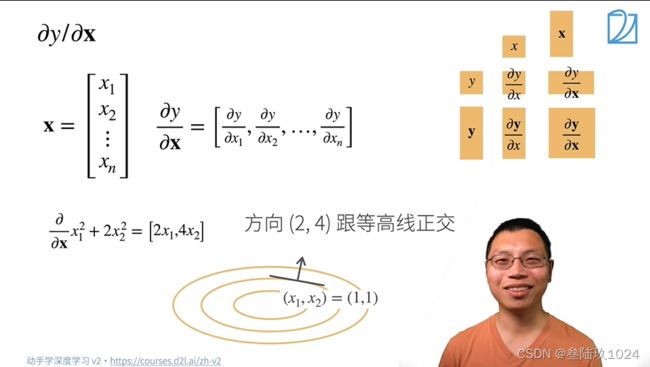
1. 标量对向量求导

2. 向量对标量求导

3. 向量对向量求导

相关知识：
矩阵论 BV1xk4y1B7RQ?p=3
分子布局

07 自动求导

autograd

向量链式求导法

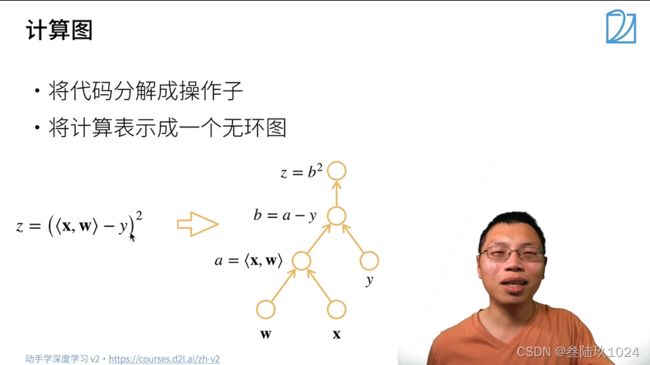
计算图

正向计算

反向累计

正反对比

练习2：在运行反向传播函数之后，立即再次运行它，看看会发生什么。

import torch
x = torch.arange(4.0,requires_grad=True)
y = 2 * torch.dot(x, x)
y.backward()
x.grad
y.backward()
x.grad
"""
RuntimeError: Trying to backward through the graph a second time (or directly access saved tensors after they have already been freed). Saved intermediate values of the graph are freed when you call .backward() or autograd.grad(). Specify retain_graph=True if you need to backward through the graph a second time or if you need to access saved tensors after calling backward.
"""

修改：

import torch
x = torch.arange(4.0,requires_grad=True)
y = 2 * torch.dot(x, x)
y.backward(retain_graph=True)
x.grad
y.backward(retain_graph=True)
x.grad
"""
tensor([ 0.,  8., 16., 24.])
"""

练习3：在控制流的例子中，我们计算d关于a的导数，如果我们将变量a更改为随机向量或矩阵，会发生什么？

def f(a):
    b = a * 2
    while b.norm() < 1000:
        b = b * 2
    if b.sum() > 0:
        c = b
    else:
        c = 100 * b
    return c
a = torch.randn(size=(3,4), requires_grad=True)
d = f(a)
d.backward()
# grad can be implicitly created only for scalar outputs

08 线性回归 （有较多概念）

chapter_linear-networks / linear_regression
线性神经网络基础知识 ：神经网络的整个训练过程，包括：定义简单的神经网络架构、数据处理、指定损失函数和如何训练模型 （包括08 09）
从简单的线性神经网络开始

相关基础概念

1. 线性回归

预测任务的一类，除了回归问题还有分类问题

基本元素

**训练数据集 / 训练集：**真实的数据集，包括试图预测的目标和预测所依据的自变量
**样本 / 数据点 / 数据样本：**每行数据
**标签 / 目标：**试图预测的目标
**特征 / 协变量：**预测所依据的自变量

2. 线性模型

1. 示例表达式：
   
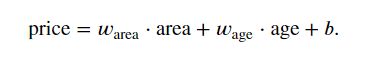
   其中
   Warea和Wage为权重，权重决定了每个特征对我们预测值的影响
   b为偏置(bias)、偏移量(offset)或截距(intercept)
   严格来说：该表达式是输入特征的一个仿射变换(affine transformation)，仿射变换的特点是通过加权和对特征进行线性变换(linear transformation)，并通过偏置项来进行平移(translation)

2. 机器学习领域
   由于我们通常使用的是高维数据集，建模时采用线性代数表示法会比较方便：
   
   其中，上述表达式中的向量x 对应于单个数据样本的特征，使用矩阵X可以很方便的引用整个数据集的样本，其中，行数代表了一个样本的特征数量，而列数代表了样本数
   上述表达式可表示为：
   

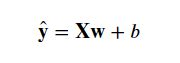
线性回归的目的找到一组权重向量w和偏置b：当给定从X的同分布中取样的新样本特征时，这组权重向量和偏置能够使得新样本预测标签的误差尽可能小

在确定模型参数(model parameters)，还需要两个东西：

1. 模型质量的度量方式
2. 通过更新模型以提高模型预测质量的方法

3. 损失函数

定义：量化目标的实际值与预测值之间的差距

损失均值：

找到一组参数(w*, b*)，使在所有训练样本上的**总损失：**最小化

4. 解析解 / 显示解 数学过程不理解

线性回归是一个很简单的优化问题，线性回归的解可以用一个公式简单地表达出来，此类解叫做解析解

虽然解析解可以进行很好的数学分析，但是解析解对问题的限制很严格，导致他无法广泛应用在深度学习中

5. 随机梯度下降

即使在无法得到解析解的情况下，仍可以有效的训练模型
在许多任务上，那些难以优化的模型效果要更好。 因此，弄清楚如何训练这些难以优化的模型是非常重要的
方法：通过不断在损失函数递减的方向上 更新参数 来降低误差
梯度下降最简单的用法：计算损失函数(数据集中所有样本的损失均值)关于模型参数的导数
但是，该方法执行时会很慢，因为在每一次更新参数前，都必须遍历整个数据集
因此，我们通常会在每次需要计算更新时，随机抽取一小批样本，这种变体就叫做 小批量随机梯度下降(minibatch stochastic gradient descent)

ppt图解：

6. 矢量化加速

对比for循环可带来数量级的加速

7. 正态分布与平方损失

正态分布的概率密度函数：

改变均值会产生沿 轴的偏移，增加方差将会分散分布、降低其峰值

没看懂的点：

8. 从线性回归到深度网络

将线性回归模型描述为一个神经网络

该图只显示连接模式，即只显示每个输入如何连接到输出，隐去了权重和偏置的值。
输入为 1,…, ， 因此输入层中的输入数（或称为特征维度，feature dimensionality）为 。 网络的输出为 1 ，因此输出层中的输出数是1。需要注意的是，输入值都是已经给定的，并且只有一个计算神经元。
由于模型重点在发生计算的地方，所以通常我们在计算层数时不考虑输入层。我们可以将线性回归模型视为仅由单个人工神经元组成的神经网络，或称为单层神经网络。

习题未做（数学相关性太大）

线性回归的从零开始实现 ？

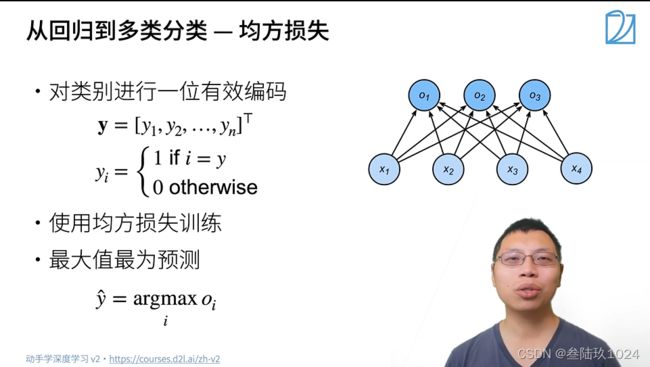
09 Softmax回归

1

04 数据操作 数据预处理

1.引入库

代码如下（示例）：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
import  ssl
ssl._create_default_https_context = ssl._create_unverified_context

2.读入数据

代码如下（示例）：

data = pd.read_csv(
    'https://labfile.oss.aliyuncs.com/courses/1283/adult.data.csv')
print(data.head())

该处使用的url网络请求的数据。

---

总结