最短路径->Dijkstra算法和Floyd算法
背景:在图的学习过程中,最短路径问题是一个肯定会遇到的问题。而这个问题的原型来源于我们实际生活中的问题,例如汽车的最优路径导航。所以为了找到解决这些实际问题的最优方案,前辈们提出了Dijkstra算法和Floyd算法,下面就来详细地了解一下这两个出名的算法。
现在,假设有V0~V6七个地方,每两个地方之间的距离入下图所示:
Dijkstra算法:O(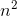 )
)
这是一种贪心算法,每次找到一条权值最小的点加入到一个集合中,该集合中的所有点已经找到源点到该点的最短距离长。主要步骤如下:
创建一个数据结构Vex,包含元素weight:记录源点到该点的暂时的最短路径长,visited:用于判断该点是否已经在集合中,path:用于记录源点到该点的最短路径。然后用一个Vex数组dis来寻找源点到各点的最短路径长。
从dis数组中每次取出一个没有被访问过的,且暂时最短路径长最小的点,将该点加入到集合中。此时,dis数组中可能有些元素需要更新。将dis数组更新。
上面的说起来有点笼统,大家可能不是很理解,接下来我们用上面的图这个实例来理解Dijkstra算法。
假设源点为V0,默认V0点已经在集合中,则此时V0到V1之间距离为6,所以dis[1].weight = 6,V0到V2之间不是直接相连,故dis[2].weight = MAX,表示V0到V2不可达,以此类推,dis[3].weight = 9,dis[4].weight = MAX,dis[5].weight = MAX,dis[6].weight = MAX。
从不在集合中的点中,选出一个距离最短的点,为V1,将dis[1].visited设置为true。之后再更新一下dis数组,因为V1点加入到了集合中,所以V0可以通过V1到达V2,所以此时dis[2].weight = 11,其他点不需更新。
之后再从剩下的点中选出一个距离最短的点,为V3,将dis[3].visited设置为true。之后再更新一下dis数组,因为V3点加入到了集合中,所以V0可以通过V3到达V4,所以此时dis[4].weight = 16,V0可以通过V3到达V5,所以此时dis[5].weight = 19,其他点不需更新。
之后再重复以上的步骤,直至所有的点都加入到集合中。
Dijkstra算法的代码实现:
struct Vex{
int weight;
bool visited;
string path;
};
/**
* Dijkstra代码实现
* @param graph 图的矩阵表示,例如graph[0][1]表示顶点0到顶点1的权值
* @param n 顶点个数
* @param start 起始顶点
*/
void Dijkstra(int graph[][7], int n, int start){
Vex dis[n];
//初始化dis数组
for (int i = 0; i < n; ++i) {
dis[i].weight = graph[start][i];
dis[i].visited = false;
dis[i].path = to_string(start) + "->" + to_string(i);
}
dis[start].visited = true;
//每次寻找一个新的顶点的最短路径
for (int j = 1; j < n; ++j) {
int index = 0;
int temp = MAXCOST;
//找到距离最近的顶点
for (int i = 0; i < n; ++i) {
if (dis[i].visited == false && temp > dis[i].weight){
index = i;
temp = dis[i].weight;
}
}
dis[index].visited = true;
//更新dis数组
for (int k = 0; k < n; ++k) {
if (!dis[k].visited) {
if (dis[k].weight > dis[index].weight + graph[index][k]) {
//修改最短路径长
dis[k].weight = dis[index].weight + graph[index][k];
//修改最短路径
dis[k].path = dis[index].path + "->" + to_string(k);
}
}
}
}
for (int l = 0; l < n; ++l) {
cout<<"点"<Floyd算法:O( )
)
这是一种动态规划算法。Dijkstra算法是求解一个点到其余点的最短路径,而Floyd算法是求解图中任意两个点之间的最短距离。相较于Dijkstra算法而言,这个算法简单直接暴力,代码只有三个简单的for循环。下面我们来分析一下Floyd算法的思路。
该算法将图的邻接矩阵copy了一份保存到了一个新的二维数组graph中,例如graph[i][j]表示顶点i到顶点j的距离。初始时的graph矩阵如下:
| 0 | 6 | ∞ | 9 | ∞ | ∞ | ∞ |
| ∞ | 0 | 5 | 2 | ∞ | ∞ | ∞ |
| ∞ | ∞ | 0 | ∞ | ∞ | ∞ | ∞ |
| ∞ | ∞ | ∞ | 0 | 7 | 10 | ∞ |
| ∞ | ∞ | ∞ | ∞ | 0 | 1 | 3 |
| ∞ | ∞ | ∞ | ∞ | ∞ | 0 | 8 |
| ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | 0 |
现在该矩阵中任何两点之间的路径不经过任何中间点,例如V0与V4点不直接相连,故graph[0][4] = ∞。而我们很容易发现,如果可以经过一个中间点,比如说V1,则任何两点之间的最短路径长可能发生变化,例如:graph[0][2]由∞变为了11。在可以经过一个中间点的情况下,变化后的矩阵如下所示:
| 0 | 6 | 11 | 9 | ∞ | ∞ | ∞ |
| ∞ | 0 | 5 | 2 | ∞ | ∞ | ∞ |
| ∞ | ∞ | 0 | ∞ | ∞ | ∞ | ∞ |
| ∞ | ∞ | ∞ | 0 | 7 | 10 | ∞ |
| ∞ | ∞ | ∞ | ∞ | 0 | 1 | 3 |
| ∞ | ∞ | ∞ | ∞ | ∞ | 0 | 8 |
| ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | 0 |
我们再来思考,如果可以经过两个中间点的话,那么是不是某两个点之间的距离能够变得更近呢?比如V0到V4,如果只经过V3点,那么两点之间的距离为16,如果能经过V1,V3两个点的话,那么两点之间的距离为15,因此我们发现如果能同时经过两个中间点,那么可能某些点之间的距离能变得更近。
因此,我们在以上的基础上,再添加一个点作为中间点。很明显,重复以上的步骤,不断的添加中间点,当所有的点都成为中间点时,我们就能知道图中每两个点之间的最短距离。
Floyd代码实现:
/**
* Floyd代码实现
* @param graph 图的矩阵表示,例如graph[0][1]表示顶点0到顶点1的权值
*/
void Floyd(int graph[][7]){
//外层循环不断的添加中间点
for (int k = 0; k < 7; ++k) {
//内存两个for循环用于更新二维数组
for (int i = 0; i < 7; ++i) {
for (int j = 0; j < 7; ++j) {
if (graph[i][j] > graph[i][k] + graph[k][j]){
graph[i][j] = graph[i][k] + graph[k][j];
}
}
}
}
for (int l = 0; l < 7; ++l) {
cout<<"点0到点"<
