回声消除AEC算法(含Matlab代码)
基于自适应滤波器的回声消除AEC算法(含Matlab代码)
- 摘要
- 自适应滤波器
- 声学回波抵消
- AEC算法解析
- LMS算法
- NLMS算法
- VSNLMS算法
- APLMS算法
- LMS-Newton算法
- PFBLMS算法
- 子带LMS算法
- 实验与结果
- 关于代码中展示模块的一点解释
摘要
本文从实用角度出发,简单介绍回声消除(AEC)背景与理论,对比评价不同自适应算法的效果。
本文提到的所有AEC算法的Matlab代码,均可以从笔者的仓库下载
Gitee项目:https://gitee.com/EthanLifeGreat/Mono_AEC
Github项目:https://github.com/EthanLifeGreat/Mono_AEC
自适应滤波器
“自适应”指的是系统试图调节其参数来达到由系统自身状态和外围参数所确定的某个明确定义的目标,其中的“系统”亦被称为“滤波器”。
一个典型的自适应滤波器可以被用于对某个系统进行建模以了解其参数,或被用于逆建模以均衡某系统产生的影响。
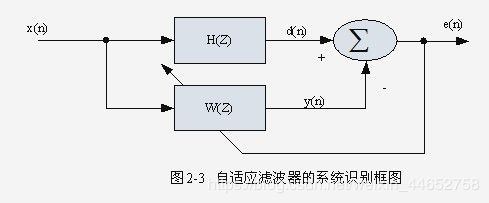
如上图,我们希望自适应滤波器 W(Z) 尽可能地模拟 系统H(Z),(表现在整个系统的输出 e(n) 接近于0)。而 e(n) 又反过来作为自适应滤波器的输入,参与滤波器的自我调节。
用现在的观点来看,自适应滤波器应属于机器学习的范畴。
声学回波抵消
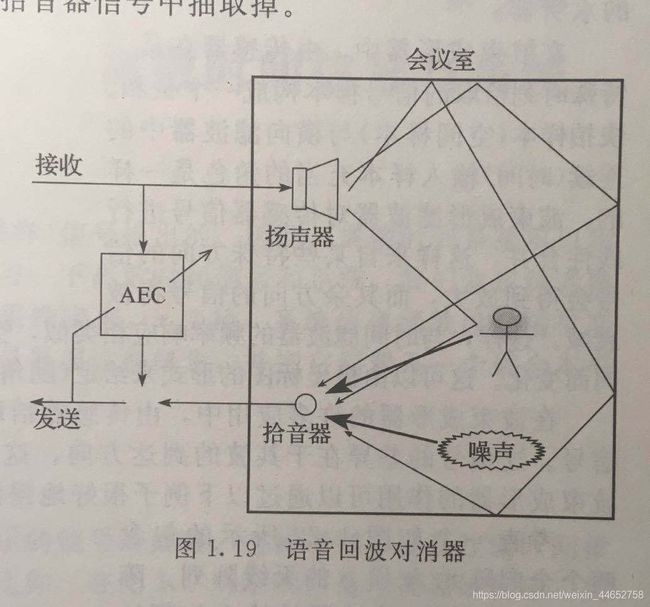
声学回波抵消(Acoustic Echo Cancellation, AEC)就是自适应滤波器的一个应用领域。
AEC的经典背景问题是会议室对话问题。
本会议室接收到远端的语音 x(n),会议室环境视作某一系统 H(Z),记其等效滤波器为 w0(n),则会议室拾音器收到的信号 d(n) 满足 d(n) = w0(n) * x(n) + r(n),其中 r(n) 为噪声,用高斯白噪声简化表示。
图中的 AEC 系统用于模拟会议室的环境,以求在会议室人不发声时,本会议室发送的信号 e(n) 接近与0,即抵消拾音器拾到的回声。
从整体上看,AEC系统的输入为远端参考信号x(n),期望信号d(n),目的是调整自己的滤波器参数 w(n),以使得自己的输出w(n)*x(n)尽量接近 d(n)
当然,以上过程要在近端(会议室)无人讲话的情况下进行。当近端人物开始讲话时,应当停止滤波器系数的更新,因为此时的 d(n) 难以满足 d(n) = w0(n) * x(n) + r(n),如不停止更新,则将产生难以预料的错误。
因此,近端无人讲话时滤波器便重复自适应步骤,以学习缓慢变化的环境,这个阶段称为适应阶段,类似于机器学习的训练;有人讲话时停止适应,用最近的参数滤波,此阶段为决策阶段,类似于机器学习的测试。
另:如果不给参考信号x,则属于盲反卷积/盲均衡问题。这不在本文讨论范围。
AEC算法解析
LMS算法
LMS算法是使用最为广泛的自适应滤波算法。其全称为最小均方(Least Mean Square)算法
算法的代价函数是 e 2 ( n ) e^2(n) e2(n). 即滤波器输出与期望信号的差的平方。
经过最陡梯度下降法的推导,算法流程如下:
- 滤波:
y ^ = w T x \hat{y}=\bf{w}^T\bf{x} y^=wTx - 误差估计:
e = d − y ^ e=d-\hat{y} e=d−y^ - 抽头权系数向量更新:
w ′ = w + 2 μ ⋅ e ⋅ x \bf{w'}=\bf{w}+2\mu\cdot e\cdot\bf{x} w′=w+2μ⋅e⋅x
其中,w为列向量,可视作FIR滤波器系数;
x为列向量,是某一片段的参考信号;
d为标量,是期望信号在该片段的最后一个分量;
y为标量,是期望信号在该片段的最后一个分量的预测值;
w‘为下一个片段(通常是当前片段整体右移一个采样点的片段)的滤波器系数;
μ \mu μ为一恒定常量,称为步长参数。
NLMS算法
NLMS全称归一化(Normalized)LMS算法,其考虑老板勃起输入端信号水平的变化,选择归一化的步长参数作为LMS算法的改进。该归一化的步长参数导致一个稳定且可以快速收敛的自适应算法,流程如下:
- 滤波:
y ^ = w T x \hat{y}=\bf{w}^T\bf{x} y^=wTx - 误差估计:
e = d − y ^ e=d-\hat{y} e=d−y^ - 抽头权系数向量更新: w ′ = w + μ ~ x T x + ψ ⋅ e ⋅ x \bf{w'}=\bf{w}+\frac{\widetilde{\mu}}{\bf{x}^T\bf{x}+\psi}\cdot e\cdot\bf{x} w′=w+xTx+ψμ ⋅e⋅x
其中参数与LMS中定义基本一致。 μ ~ \widetilde{\mu} μ 与 ψ \psi ψ是需要适当选择的正常数,这在代码中给出了范例。
VSNLMS算法
VSNLMS算法在在NLMS基础上时变步长参数 μ ~ \widetilde{\mu} μ ,称为可变步长的NLMS算法。
此时步长参数是滤波器输出与期望信号能量比的负系数线性函数。
μ ~ ( n ) = 1 − η E [ y ^ 2 ( n ) ] E [ d 2 ( n ) ] \widetilde{\mu}(n)=1-\eta\frac{E[\hat{y}^2(n)]}{E[{d}^2(n)]} μ (n)=1−ηE[d2(n)]E[y^2(n)]
这样可以在面对非平稳且高度色化的语音信号具有更快的收敛性能。算法流程如下:
- 滤波:
y ^ = w T x \hat{y}=\bf{w}^T\bf{x} y^=wTx - 误差估计:
e = d − y ^ e=d-\hat{y} e=d−y^ - 步长计算:
σ d 2 ( n ) = α σ d 2 ( n − 1 ) + ( 1 − α ) d 2 ( n ) \sigma^2_d(n)=\alpha\sigma^2_d(n-1)+(1-\alpha)d^2(n) σd2(n)=ασd2(n−1)+(1−α)d2(n)
σ y ^ 2 ( n ) = α σ y ^ 2 ( n − 1 ) + ( 1 − α ) y ^ 2 ( n ) \sigma^2_{\hat{y}}(n)=\alpha\sigma^2_{\hat{y}}(n-1)+(1-\alpha){\hat{y}}^2(n) σy^2(n)=ασy^2(n−1)+(1−α)y^2(n)
μ ~ ( n ) = 1 − η σ y ^ 2 ( n ) σ d 2 ( n ) \widetilde{\mu}(n)=1-\eta\frac{\sigma^2_{\hat{y}}(n)}{\sigma^2_d(n)} μ (n)=1−ησd2(n)σy^2(n)
if μ ~ ( n ) > 1 \widetilde{\mu}(n)>1 μ (n)>1, μ ~ ( n ) = 1 \widetilde{\mu}(n)=1 μ (n)=1
if μ ~ ( n ) < 0 \widetilde{\mu}(n)<0 μ (n)<0, μ ~ ( n ) = 0 \widetilde{\mu}(n)=0 μ (n)=0 - 抽头权系数向量更新: w ′ = w + μ ~ ( n ) x T x + ψ ⋅ e ⋅ x \bf{w'}=\bf{w}+\frac{\widetilde{\mu}(n)}{\bf{x}^T\bf{x}+\psi}\cdot e\cdot\bf{x} w′=w+xTx+ψμ (n)⋅e⋅x
其中 σ \sigma σ表示短时平均值,需要如上逐点递推。
APLMS算法
APLMS算法全称仿射投影(Affine Projection)LMS算法,由于其实质上是NLMS的推广,故亦称为广义NLMS算法。
APLMS与NLMS的联系在于,前者是高维度版的NLMS算法,即输入x从列向量变为矩阵,同时输出 y ^ \hat{y} y^及e从标量变为行向量。其流程如下:
- 滤波:
y ^ = X T w \hat{\bf{y}}=\bf{X}^T\bf{w} y^=XTw
y ^ \hat{y} y^是 y ^ \hat{\textbf{y}} y^ 的第一个分量 - 误差估计:
e = d − y ^ \bf{e}=\bf{d}-\bf{\hat{y}} e=d−y^ - 抽头权系数向量更新: w ′ = w + μ ~ X ( X T X + ψ I ) − 1 e \bf{w'}=\bf{w}+{\widetilde{\mu}}\bf{X}(\bf{X}^T\bf{X}+\psi\bf{I})^{-1}\bf{e} w′=w+μ X(XTX+ψI)−1e
其中。
其中参数与NLMS中定义类似,
w \bf{w} w为列向量,可视作FIR滤波器系数;
X \bf{X} X为矩阵,N行M列,代表是M个长度为N的片段的参考信号;
d \bf{d} d为列向量,是每一个期望信号片段的最后一个分量;
y \bf{y} y为列向量,是为对应 d \bf{d} d的预测值;
w ′ \bf{w}^{'} w′为下一个片段(通常是当前片段整体右移一个采样点的片段)的滤波器系数;
μ ~ {\widetilde{\mu}} μ 为一恒定常量,称为步长参数。
I \bf{I} I为M*M单位矩阵
显然,当M=1时,APLMS退化为NLMS算法。
后面将看到,APLMS算法有着更好的收敛特性,也有着难以驾驭的时间复杂度。
LMS-Newton算法
不同于最陡梯度下降法,Newton法的梯度向量指向性能表面最小点,而非最陡梯度方向。这或有利于获得好得多的收敛性能。

LMS-Newton算法流程与LMS基本一致,唯一不同在于第三步的抽头权系数向量更新,公式为:
w ′ = w + 2 μ e ⋅ R ^ x x − 1 x \bf{w'}=\bf{w}+2\mu e\cdot\bf{\hat{R}^{-1}_{xx}}\bf{x} w′=w+2μe⋅R^xx−1x
其中 R ^ x x − 1 \bf{\hat{R}^{-1}_{xx}} R^xx−1为输入相关矩阵 E [ x x T ] E[\bf{x}\bf{x}^T] E[xxT]的一个估计。
在具体实现时,不对 R ^ x x − 1 \bf{\hat{R}^{-1}_{xx}} R^xx−1进行直接估计,而是引入格型预测器,以实现更便捷的计算。此处不作展开。
PFBLMS算法
PFBLMS全称分割的频域分块(Partitioned Frequency-Based)LMS算法,与核心内容还是LMS算法,但是有如下改进:
基于数据集合的并行处理,块处理技术可以显著地减小自适应滤波器的计算复杂性。
频域计算(或称为快速计算)利用离散傅里叶变换性质,用对应元素乘积替代循环卷积。
分割的FBLMS有利于减少时延,尤其是在滤波器长度很大时。
子带LMS算法
子带(Subband)LMS算法也属于分块/并行处理算法,其核心思想是让频域上的各个子带进行自适应,每个子带有自己的滤波器参数。
示例代码中使用的是如下的综合独立结构。
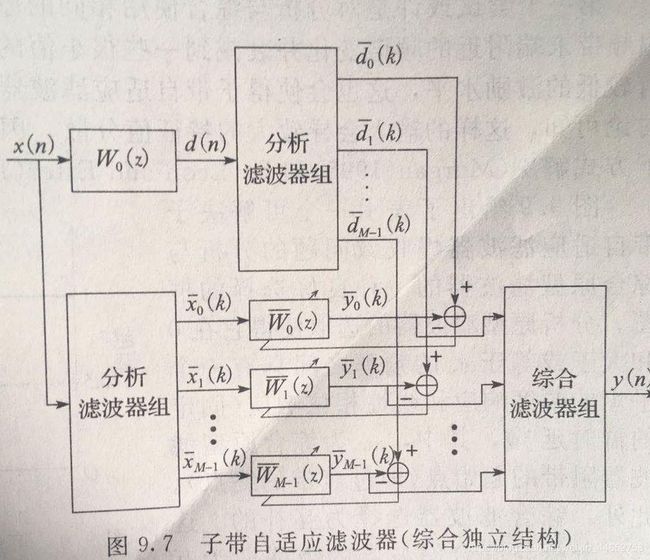
由于滤波器组难以理想地互补,综合独立结构的滤波器具有一定的失真,这也会在后面的实验中体现。
尽管另一选择——综合相关结构,可以减小这种失真,但此结构又会引入时延与不稳定的问题,而不那么受到欢迎。
实验与结果

实验内容是一段英文广播内容,长度30秒。使用的回声是一个680点时延的双脉冲单位脉冲响应。(尽管这与会议室模型常见的回声参数不一致,但却十分浅显,易于辨别)
-
从这张图来看,子带LMS法似乎是最好的选择,但其在原书配套资料中的结果却原没有这里这个实验的效果好,甚至是原书作者给出了“最差”的评价。笔者目前也没有探究出原因。
-
其后是放射投影法(VSAPLMS),收敛速度最快,或认为其可以在更短的样本上学习到更精确的参数。但它的运算量巨大,耗时长:笔者的PC机上(第九代酷睿i3),30秒的音频运行时间超过10秒。
-
再之后,Newton法和PFBLMS的收敛速度似乎不相上下。但就运算时间而言,后者要略胜一筹。时间大致上为1.5秒内与1秒内。
-
收敛速度最后的应该是最简单的NLMS算法无疑,但其计算速度较快,整体上可以与PFBLMS相媲美。
关于代码中展示模块的一点解释
由于代码中前三种算法(NLMS, NLMS-Newton, APLMS)的学习目标都是回声的等效滤波器,这三种算法都可以依据期望信号和学习到的滤波器参数w恢复出原信号 x ^ \hat{x} x^(xhat),而其它的算法只能正向计算(由x到 y ^ \hat{y} y^(yhat)),不能逆向检验结果。
使用前三种算法时,可以尝试播放原信号x,带回声和噪声信号d,恢复后的原信号xhat,拟合的带回声信号yhat,以及对消后信号e,感受效果。