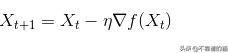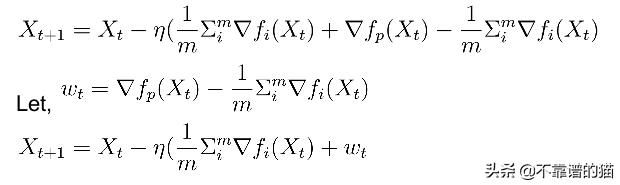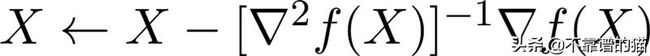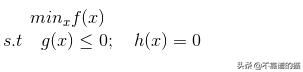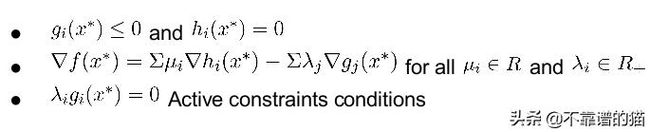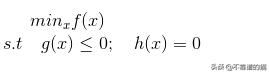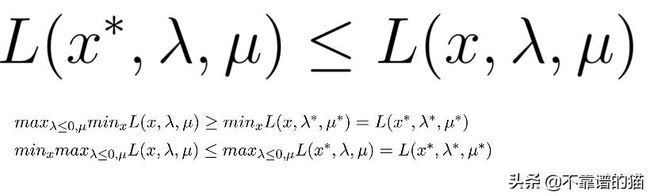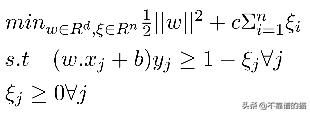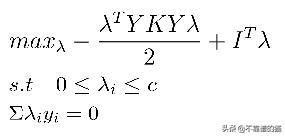支持向量机(SVM)的约束和无约束优化、理论和实现

http://blog.itpub.net/29829936/viewspace-2636249/

 

2019-02-16 21:59:23

 

优化是机器学习领域最有趣的主题之一。我们日常生活中遇到的大多数问题都是通过数值优化方法解决的。在这篇文章中，让我们研究一些基本的数值优化算法，以找到任意给定函数(这对于凸函数最有效)的局部最优解。让我们从简单的凸函数开始，其中局部和全局最小值是相同的，然后转向具有多个局部和全局最小值的高度非线性函数。

整个优化围绕线性代数和微积分的基本概念展开。最近的深度学习更新引起了数值和随机优化算法领域的巨大兴趣，为深度学习网络所展示的惊人定性结果提供了理论支持。在这些类型的学习算法中，没有任何明确已知的优化函数，但我们只能访问0阶和1阶的Oracles。Oracles是在任何给定点返回函数值（0阶），梯度（1阶）或Hessian（2阶）的黑盒子。本本提供了对无约束和约束优化函数的基本理论和数值理解，还包括它们的python实现。

一个点成为局部最小值的必要和充分条件：

设f(.)是一个连续的二阶可微函数。对于任一点为极小值，它应满足以下条件:

 

• 一阶必要条件:

 

• 二阶必要条件：

 

• 二阶充足条件：

 

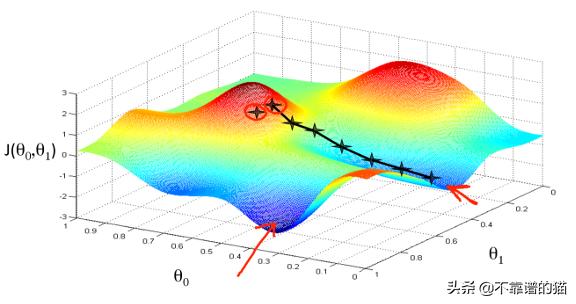
梯度下降：

梯度下降是学习算法(机器学习、深度学习或深度强化学习)领域所有进展的支柱。在这一节中，我们将看到为了更快更好的收敛，梯度下降的各种修改。让我们考虑线性回归的情况，我们估计方程的系数:

 

假设该函数是所有特征的线性组合。通过最小化损失函数来确定最佳系数集：

 

这是线性回归任务的最大似然估计。最小二乘法(Ordinary Least Square)涉及到求特征矩阵的逆，其表达式为:

 

对于实际问题，数据的维数很大，很容易造成计算量的激增。例如,让我们考虑问题的图像特征分析:一般图像的大小1024 x1024,这意味着特征的数量级为10⁶。由于具有大量的特征，这类优化问题只能通过迭代的方式来解决，这就导致了我们所熟知的梯度下降法和牛顿-拉弗森法。

 

梯度下降算法：

 

梯度下降算法利用先前指定的学习率（eta）在负梯度的方向（最陡的下降方向）上更新迭代（X）。学习率用于在任何给定的迭代中防止局部最小值的overshoot。

下图显示了函数f（x）=x²的梯度下降算法的收敛性，其中eta = 0.25

 

找出一个最优eta是目前的任务，这需要事先了解函数的理解和操作域。

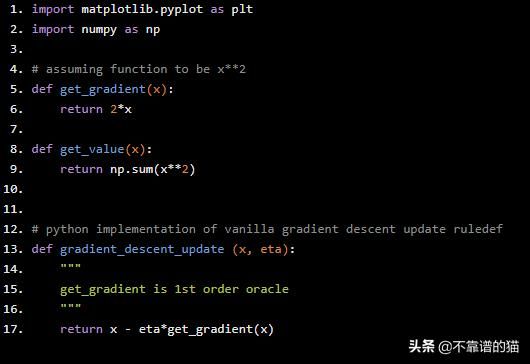
import matplotlib.pyplot as plt
import numpy as np
# assuming function to be x**2
def get_gradient(x):
 return 2*x
def get_value(x):
 return np.sum(x**2)
# python implementation of vanilla gradient descent update ruledef​ ​ 
def gradient_descent_update​ (x, eta):
 """
 get_gradient is 1st order oracle
 """
 return​ x - eta*get_gradient(x)

 

Armijo Goldstein条件梯度下降:

为了减少手动设置的工作，应用Armijo Goldstein (AG)条件来查找下一个迭代的(eta)。AG条件的形式推导需要线性逼近、Lipchitz条件和基本微积分的知识。

我们定义两个函数f1(x)和f2(x)作为两个不同系数和的f(x)的线性逼近，其具有两个不同的系数α和β，由下式给出：

 

在AG条件的每次迭代中，满足以下关系的特定eta：

 

找到并且相应地更新当前迭代。

下图显示了下一次迭代的范围，对于函数f（x）=x²的收敛，alpha = 0.25，beta = 0.5：

 

上图中红色、蓝色和绿色的线对应于绿色显示的下一个可能迭代的范围。

# python implementation of gradient descent with AG condition update rule
def gradient_descent_update_AG(x, ​ alpha​ =0.5, ​ beta​ =0.25):
 eta​ =0.5
 max_eta​ =np.inf
 min_eta​ =0.
 value = get_value(x)
 grad = get_gradient(x)
 while​ ​ True​ :
 x_cand = x - (eta)*grad
 f = get_value(x_cand)
 f1 = value - eta​ *a​ lpha*np.sum(np.abs(grad)*​ *2​ )
 f2 = value - eta​ *be​ ta *np.sum(np.abs(grad)*​ *2​ )
 if​ f<=f2 ​ and​ f>=f1:
 return x_cand
 if f <= f1:
 if eta == max_eta:
 eta = np.min([2.*eta, eta + max_eta/2.])
 else:
 eta = np.min([2.*eta, (eta + max_eta)/2.])
 if​ f>=f2:
 max_eta = eta
 eta = (eta+min_eta)/2.0

 

完全松弛条件的梯度下降：

在完全松弛条件的情况下，新的函数g（eta）被最小化以获得随后用于寻找下一次迭代的eta。

 

此方法涉及解决查找每个下一个迭代的优化问题，其执行方式如下：

 

# The python implementation for FR is shown below:
def​ ​ gradient_descent_update_FR​ (x):
 eta = ​ 0.5
 thresh = ​ 1e-6
 max_eta = np.inf
 min_eta = ​ 0.
 while​ ​ True​ :
 x_cand = x - eta*get_gradient(x)
 g_diff = ​ -1.​ *get_gradient(x)*get_gradient(x_cand)
 if​ np.sum(np.abs(g_diff)) < thresh ​ and​ eta > ​ 0 ​:
 return​ x_cand
 if g_diff > 0:
 if eta == max_eta:
 eta = np.min([2.*eta, eta + max_eta/2.])
 else:
 eta = np.min([2.*eta, (eta + max_eta)/2.])
 else:
 max_eta = eta
 eta = (min_eta + eta)/2.0

 

随机梯度下降

我们知道，在实际设置中，数据的维数会非常大，这使得对所有特征进行进一步的梯度计算非常昂贵。在这种情况下，随机选择一批点(特征)并计算期望的梯度。整个过程的收敛只是在预期的意义上。

在数学上它意味着：随机选择一个点（p）来估计梯度。

 

在上面的迭代中，wt可以被视为噪声。只有当E（wt）趋于0时，该迭代才会导致局部最优。

 

同样，可以看出wt的方差也是有限的。通过以上证明，保证了SGD的收敛性。

# SGD implementation in python
def​ ​ SGD​ (self, X, Y, batch_size, thresh=​ 1 ​ ):
 loss = ​ 100
 step = ​ 0
 if​ self.plot: losses = []
 while​ loss >= thresh:
 # mini_batch formation
 index = np.random.randint(​ 0 ​ , len(X), size = batch_size)
 trainX, trainY = np.array(X)[index], np.array(Y)[index]
 
 self.forward(trainX)
 loss = self.loss(trainY)
 self.gradients(trainY)
 # update
 self.w0 -= np.squeeze(self.alpha*self.grad_w0)
 self.weights -= np.squeeze(self.alpha*self.grad_w)
 
 if self.plot: losses.append(loss)
 if​ step % ​ 1000​ == ​ 999​ : ​ 
 print​ ​ "Batch number: {}"​ .format(step)+​ " current loss: {}"​ .format(loss)
 step += ​ 1
 if​ self.plot : self.visualization(X, Y, losses)
 pass

 

AdaGrad

Adagrad是一个优化器，可帮助自动调整优化问题中涉及的每个特征的学习率。这是通过跟踪所有梯度的历史来实现的。该方法也仅在期望意义上收敛。

def​ ​ AdaGrad​ (self, X, Y, batch_size,thresh=0.5​ ,epsilon=1e-6​ ):
 loss = ​ 100
 step = ​ 0
 if​ self.plot: losses = []
 G = np.zeros((X.shape[​ 1 ​ ], X.shape[​ 1 ​ ]))
 G0 = ​ 0
 while​ loss >= thresh:
 # mini_batch formation
 index = np.random.randint(​ 0 ​ , len(X), size = batch_size)
 trainX, trainY = np.array(X)[index], np.array(Y)[index]
 self.forward(trainX)
 loss = self.loss(trainY)
 self.gradients(trainY)
 G += self.grad_w.T*self.grad_w
 G0 += self.grad_w0**​ 2
 den = np.sqrt(np.diag(G)+epsilon)
 delta_w = self.alpha*self.grad_w / den
 delta_w0 = self.alpha*self.grad_w0 / np.sqrt(G0 + epsilon)
 # update parameters
 self.w0 -= np.squeeze(delta_w0)
 self.weights -= np.squeeze(delta_w)
 if self.plot: losses.append(loss)
 if​ step % ​ 500​ == ​ 0 ​ : ​ 
 print​ ​ "Batch number: {}".format (step)+​ " current loss: {}"​.format(loss)
 
 step += ​ 1
 if​ self.plot : self.visualization(X, Y, losses)
 pass

 

让我们转向基于Hessian的方法，牛顿和拟牛顿方法：

基于hessian的方法是基于梯度的二阶优化方法，几何上涉及到梯度和曲率信息来更新权重，因此收敛速度比仅基于梯度的方法快得多，牛顿方法的更新规则定义为:

 

该算法的收敛速度远快于基于梯度的方法。数学上,梯度下降法的收敛速度正比于O (1 / t),而对于牛顿法它正比于O (1 / t²)。但是对于高维数据，为每个迭代估计二阶oracle的计算成本很高，这导致使用一阶oracle模拟二阶oracle。这就给出了拟牛顿算法。这类拟牛顿法中最常用的算法是BFGS和LMFGS算法。在这一节中，我们只讨论BFGS算法，它涉及到对函数Hessian的rank one矩阵更新。该方法的总体思想是随机初始化Hessian，并使用rank one更新规则在每次迭代中不断更新Hessian。数学上可以表示为:

 

# python implementation for BFGS
def​ ​ BFGS_update​ (H, s, y):
 smooth = ​ 1e-3
 s = np.expand_dims(s, axis= ​ -1​ )
 y = np.expand_dims(y, axis= ​ -1​ )
 rho = ​ 1.​ /(s.T.dot(y) + smooth)
 p = (np.eye(H.shape[​ 0 ​ ]) - rho*s.dot(y.T))
 return​ p.dot(H.dot(p.T)) + rho*s.dot(s.T)
def​ ​ quasi_Newton​ (x0, H0, num_iter=​ 100​ , eta=​ 1 ​ ):
 xo, H = x0, H0
 for​ _ ​ in​ range(num_iter):
 xn = xo - eta*H.dot(get_gradient(xo))
 y = get_gradient(xn) - get_gradient(xo)
 s = xn - xo
 H = BFGS_update(H, s, y)
 xo = xn
 return​ xo

 

约束优化

 

现在，是时候讨论一些围绕约束优化(包括问题的制定和解决策略)的关键概念了。本节还将讨论一种称为SVM(支持向量机)的算法的理论和Python实现。当我们在现实生活中遇到问题时，提出一个理想的优化函数是相当困难的，有时是不可行的，所以我们通过对问题施加额外的约束来放松优化函数，优化这个约束设置将提供一个近似，我们将尽可能接近问题的实际解决方案，但也是可行的。求解约束优化问题的方法有拉格朗日公式法、惩罚法、投影梯度下降法、内点法等。在这一节中，我们将学习拉格朗日公式和投影梯度下降法。本节还将详细介绍用于优化CVXOPT的开源工具箱，并介绍使用此工具箱的SVM实现。

约束优化问题的一般形式：

 

其中f(x)为目标函数，g(x)、h(x)分别为不等式约束和等式约束。如果f(x)是凸的约束条件形成一个凸集，(即g(x)为凸函数h(x)为仿射函数），该优化算法保证收敛于全局最小值。对于其他问题，它收敛于局部极小值。

投影梯度下降

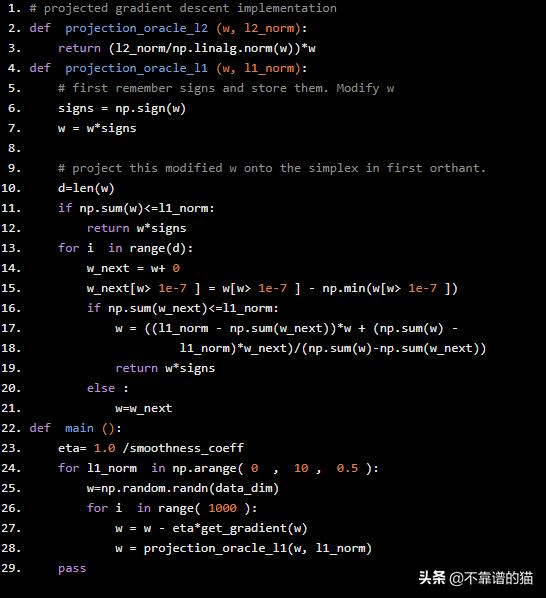
求解约束优化设置的第一步(也是最明显的一步)是对约束集进行迭代投影。这是求解约束优化问题中最强大的算法。这包括两个步骤(1)在最小化(下降)方向上找到下一个可能的迭代，(2)在约束集上找到迭代的投影。

 

# projected gradient descent implementation
def​ ​ projection_oracle_l2​ (w, l2_norm):
 return​ (l2_norm/np.linalg.norm(w))*w
def​ ​ projection_oracle_l1​ (w, l1_norm):
 # first remember signs and store them. Modify w
 signs = np.sign(w)
 w = w*signs
 
 # project this modified w onto the simplex in first orthant.
 d=len(w)
 if​ np.sum(w)<=l1_norm:
 return​ w*signs
 for​ i ​ in​ range(d):
 w_next = w+​ 0
 w_next[w>​ 1e-7​ ] = w[w>​ 1e-7​ ] - np.min(w[w>​ 1e-7​ ])
 if​ np.sum(w_next)<=l1_norm:
 w = ((l1_norm - np.sum(w_next))*w + (np.sum(w) -
 l1_norm)*w_next)/(np.sum(w)-np.sum(w_next))
 return​ w*signs
 else​ :
 w=w_next
def​ ​ main​ ():
 eta=​ 1.0 /smoothness_coeff
 for​ l1_norm ​ in​ np.arange(​ 0 ​ , ​ 10​ , ​ 0.5​ ):
 w=np.random.randn(data_dim)
 for​ i ​ in​ range(​ 1000​ ):
 w = w - eta*get_gradient(w)
 w = projection_oracle_l1(w, l1_norm)
 pass

 

了解拉格朗日公式

在大多数优化问题中，找到约束集上迭代的投影是一个困难的问题(特别是在复杂约束集的情况下)。它类似于在每次迭代中解决优化问题，在大多数情况下，优化问题是非凸的。在现实中，人们试图通过解决对偶问题而不是原始问题来摆脱约束。

在深入拉格朗日对偶和原始公式之前，让我们先了解一下KKT条件及其意义

• 对于任意点为具有等式约束的局部/全局最小值:

 

• 类似地，不等式约束:

 

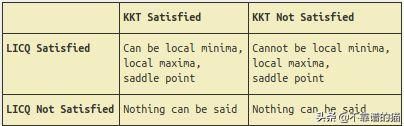
这两个条件可以很容易地通过将单位圆看作一个约束集来观察。在第一部分中，我们只考虑一个(mu)符号不重要的边界，这是等式约束的结果。在第二种情况下，考虑一个单位圆的内部集合，其中-ve符号表示(lambda)，表示可行解区域。

KKT (Karush-Kuhn-Tucker)条件被认为是一阶必要条件，当一个点被认为是一个平稳点(局部极小点、局部极大点、鞍点)时，该条件必须满足。x ^ * 是局部最小值：

 

LICQ条件:所有活动约束

 

它们应该是线性无关的。

 

拉格朗日函数

对于任何函数f (x)与不等式约束g_i (x)≤0和等式约束h_i (x) = 0,拉格朗日L (x λμ)

 

优化函数：

 

以上优化相当于：

 

上面的公式被游戏理论的主张称为原始问题（p ^ *）（即第二个玩家将总是有更好的优化机会），可以很容易地看出：

 

这个公式被称为对偶问题(d ^ *)。

当且仅当目标函数为凸且约束集为凸时，原始公式和对偶公式的最优值相同。这项要求的证明理由如下:

函数是凸的，这意味着

 

SVM（支持向量机）

 

SVM属于用于分类和回归问题的监督机器学习算法类。SVM易于扩展，可以解决线性和非线性问题（通过使用基于核的技巧）。在大多数问题中，我们无法对两类不同的数据进行单独的区分，因此我们需要在决策边界的构建中提供一点余地，这很容易用SVM来表示。支持向量机的思想是在两组不同的数据点之间创建分离的超平面。一旦获得了分离超平面，对其中一个类中的数据点(测试用例)进行分类就变得相对容易了。支持向量机甚至可以很好地用于高维数据。与其他机器学习（ML）模型相比，svm的优点是内存效率高、准确、快速。我们来看看支持向量机的数学

SVM原始问题

 

使用拉格朗日算法的SVM对偶问题

 

Derivation of Dual

 

CVXOPT

在本节中，我们将讨论使用CVXOPT库在python中实现上述SVM对偶算法。

CVXOPT通用格式的问题

 

# SVM using CVXOPT
import​ numpy ​ as​ np
from​ cvxopt ​ import​ matrix,solvers
def​ ​ solve_SVM_dual_CVXOPT​ (x_train, y_train, x_test):
 """
 Solves the SVM training optimisation problem (the Arguments:
 x_train: A numpy array with shape (n,d), denoting R^d.
 y_train: numpy array with shape (n,) Each element
 x_train: A numpy array with shape (m,d), denoting dual) using cvxopt.
 
 n training samples in takes +1 or -1
 m test samples in R^d.
 Limits:
 n<200, d<100, m<1000
 
 Returns:
 y_pred_test : A numpy array with shape (m,). This is the result of running the learned model on the
 test instances x_test. Each element is +1 or -1.
 """
 n, d = x_train.shape
 c = ​ 10​ ​ # let max lambda value be 10
 y_train = np.expand_dims(y_train, axis=​ 1 ​ )*​ 1.
 P = (y_train * x_train).dot((y_train * x_train).T)
 q = -1.​ *np.ones((n, ​ 1 ​ ))
 G = np.vstack((np.eye(n)*​ -1​ ,np.eye(n)))
 h = np.hstack((np.zeros(n), np.ones(n) * c))
 A = y_train.reshape(​ 1 ​ , ​ -1​ )
 b = np.array([​ 0.0​ ])
 P = matrix(P); q = matrix(q)
 G = matrix(G); h = matrix(h)
 A = matrix(A); b = matrix(b)
 sol = solvers.qp(P, q, G, h, A, b)
 lambdas = np.array(sol[​ 'x'​ ])
 w = ((y_train * lambdas).T.dot(x_train)).reshape(​ -1​ , ​ 1 ​ )
 b = y_train - np.dot(x_train, w)
 prediction = ​ lambda​ x, w, b: np.sign(np.sum(w.T.dot(x) + b))
 y_test = np.array([prediction(x_, w, b) ​ for​ x_ ​ in​ x_test])
 return​ y_test
if​ __name__ == ​ "__main__"​ :
 # Example format of input to the functions
 n=​ 100
 m=​ 100
 d=​ 10
 x_train = np.random.randn(n,d)
 x_test = np.random.randn(m,d)
 w = np.random.randn(d)
 y_train = np.sign(np.dot(x_train, w))
 y_test = np.sign(np.dot(x_test, w))
 y_pred_test = solve_SVM_dual_CVXOPT(x_train, y_train, x_test)
 check1 = np.sum(y_pred_test == y_test)
 print​ (​ "Score: {}/{}"​ .format(check1, len(y_Test)))