【学习笔记】密码学入门(3) 密钥,随机数,PGP软件

【学习笔记】密码学入门(3) 密钥,随机数,PGP软件

密钥

密钥本身大小并不重要,重要的是密钥空间,足够大的密钥空间才能防止暴力破解.

对称密码和公钥密码用于确保机密性的密钥,防止消息泄露;消息认证码的密钥和数字签名的密钥用于认证的密钥防止篡改和伪造.

• 会话密钥
  每次通信只使用一次的密钥
  当我们访问https://开头的网页时,web服务器和浏览器之间会基于SSL/TLS的加密通信.这样每次通信密钥都在变化提高安全性.
• 主密钥
  一直被重复使用的密钥

密钥管理

• 生成密钥
  一般用随机数生成器生成密钥,分为真随机数和伪随机数生成器.
• 配送密钥
  可以事先共享密钥,使用密钥分配中心或者公钥密码解决密钥配送问题
• 更新密钥
  利用单向散列函数更新密钥,利用这次密钥的散列值作为下次密钥,同时保证了后向安全,防止破译过去的通信内容.
• 保存密钥
  将密钥加密后保存,用于加密密钥的密钥称为KEK（Key Encrypting Key).可以通过这样降低密钥数量,例如上面提到的主密钥.
• 作废密钥

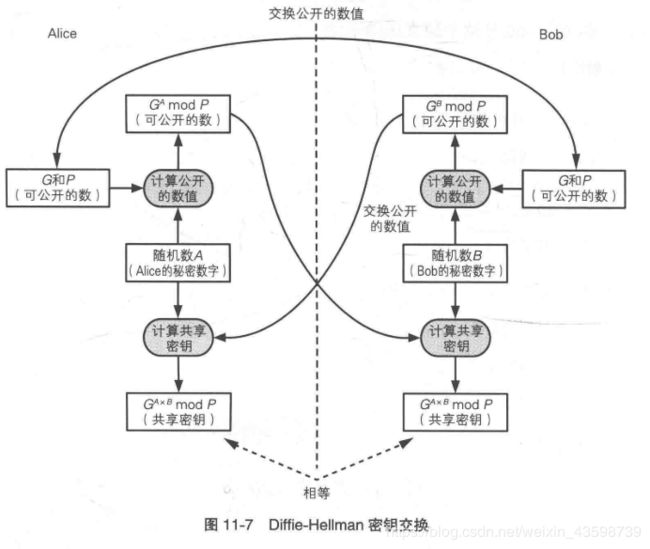
Diffie-Hellman密钥交换

通信双方仅通过交换一些公开的信息生成一个共享的密钥.

算法结构

• Alice给Bob发送两个质数P和G
• Alice和Bob各生成一个1~(p-2)之间的随机数A和B不告诉彼此
• A把 $G^{A}modP$发送给Bob,Bob把$G^{A}modP$发送给Alice.
• Alice用来自Bob的数求A次方后得到密钥,同样Bob可以计算B次方得到同样密钥
  Alice的密钥:
  $$(G^{B}modP{)}^{A}modP=G^{A\ast B}modP$$
  Bob的密钥:
  $$(G^{A}modP{)}^{B}modP=G^{A\ast B}modP$$
  所以Alice的密钥和Bob的密钥相同.
• 总结
  公开的数据有:P,G,$G^{A}modP$,$G^{B}modP$,但是根据这些数很难反推出A 和 B.称为有限域的离散对数问题,所以密钥是安全的.

生成元

在mod运算中,存在质数P和G,其中G满足G的1到(P-1)次方modP之后的结果都不一样,可以遍历1-(P-1)的任意数字,则可以称作G是P的一个生成元.例如下图中,P=13,2,6,7,11都为生成元.

但是需要注意的是1~(P-1)之间的任何一个G的P-1次方modP的结结果都是1,所以在实际中Alice 和 Bob 取得随机数是在1-(P-2)之间.
所以当G是P的生成元时,1~(P-1)之间的随机数A便和G^AmodP存在一一对应的关系.所以最终Alice和Bob的密钥存在唯一值.

同时相比于利用有限域的离散对数问题,也可以利用椭圆曲线构造Diffie-Hellman算法.

基于口令的密码

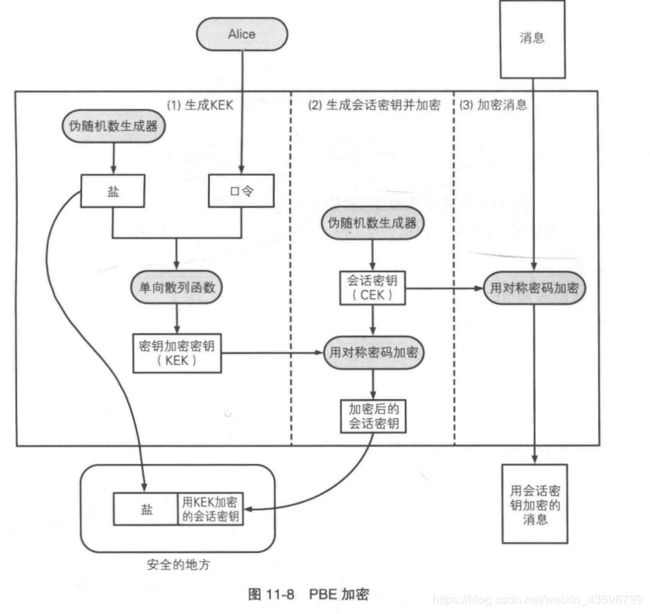
基于口令的密钥(Password Based Encryption,PBE)就是一种根据口令生成密钥并用该密钥加密的方法.逻辑如下:

可以总结为三个步骤:

• 生成KEY
  通过口令加上**盐(Salt,防御字典攻击的随机数)**经过单向散列函数产生的散列值就是用于加密密钥的KEK.
• 生成会话密钥并加密
  用随机数生成器生成会话密钥用于加密消息,即会KEK.会话密钥需要通过第一步生成的KEK加密,然后和盐保存在安全的地方.KEK加密后就可以丢弃,因为通过盐和口令就可以重建KEK.
• 加密消息
  用上述的绘画密钥加密消息.
• 总结
  加密后的产生的数据有:盐,用KEK加密后的会话密钥,用会话密钥加密的消息.
  
  同样,PBE解密也有三个步骤:
• 重建KEK
• 解密会话密钥
• 解密消息

盐的作用

盐是用来防御字典攻击的,字典攻击就是一种事先进行计算准备好了候选密钥列表的方法,因为口令一般比较简短且容易破解.所以加入盐之后,候选KEK的数量会变多.

总结

最终,口令是靠人脑记忆,盐和加密后的CEK通过武力方式保存,比如存储卡中,在使用时,通过盐和口令获得KEK,然后用KEK解密CEK,再解密消息.
可以通过拉伸改良PBE,即通过多次单向散列函数生成KEK,这样得到的KEK强度高于只经过一次单向散列函数的KEK.

随机数

前面提到的随机数主要用于:

• 生成密钥:对称密码和消息认证码
• 生成密钥对:公钥密码和数字签名
• 其他用途:生成初始化变量,生成盐等

随机数的性质:

• 随机性
  不存在统计学偏差,每个数出现的概率相同,且序列是无序的,例如给定的随机比特流样本中，1的数量大致等于0的数量，同理，“10”“01”“00”“11”四者数量大致相等,可以认为是具备统计学随机性.
• 不可预测性
  在攻击者知道过去生成的伪随机数列的前提下,依然无法预测出下一个伪随机数.
• 不可重现性
  无法重现和某一随机序列相同的数列性质,除了序列本身重现该数列.凡是有周期的序列都不具备不可重现性.
  
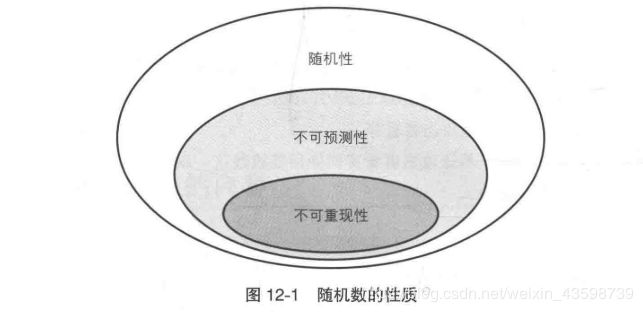
  这三条性质越往下越严格,所以可以根据三种性质分为:“弱随机数”,“强伪随机数”,“真随机数”.

伪随机数生成器

伪随机数生成器一般具有"内部状态",然后根据外部输入的"种子"来生成伪随机数列.对伪随机数的攻击也是建立在对种子以及随机数池的攻击,所以对种子以及随机数池需要进行保护.

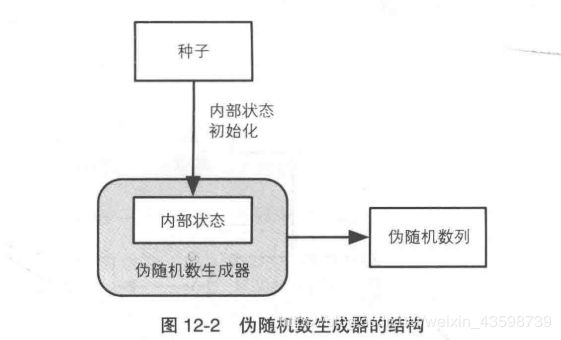
• 内部状态
  伪随机数生成器所管理的内存中的数值,因为内部状态决定了下一时刻的伪随机数列,所以内部状态不能被攻击者知道.
• 种子(seed)
  种子是用来对伪随机数生成器的内部状态进行初始化的,是一串随机的比特序列,伪随机数生成器是公开的,但是种子是保密的.

伪随机数生成算法

• 线性同余法
  将当前的伪随机数值乘以A再加上C,然后将除以M得到的余数作为下一个伪随机数,所以内部状态即最近一次生成的伪随机数的值.
  但是不可以应用于密码技术,因为产生的随机数不具备不可预测性.
• 单向散列函数(Hash)
  单向散列函数可以产生具有不可预测性的伪随机数列,即强伪随机数.因为单向散列函数的单向性,所以伪随机数具有不可预测性.
  
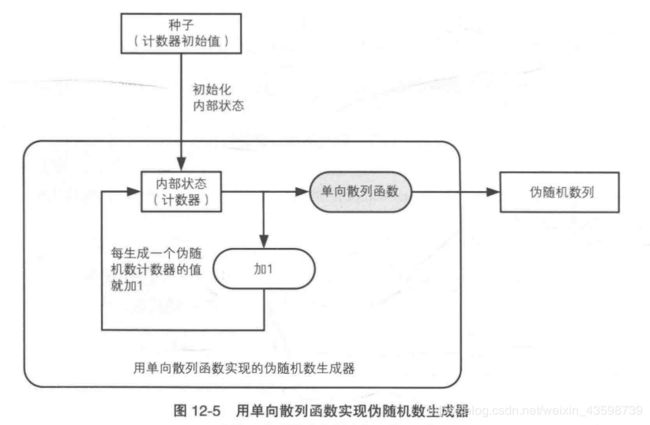
• 密码法生成伪随机数
  即用加密算法代替单向散列函数,把内部状态通过AES或者RSA加密算法加密后生成伪随机数，密码的机密性支撑了伪随机数的不可预测性．
• 其他算法
  ANSI X9.17算法
  
  还有梅森旋转算法等,但是需要注意的是,一个随机数算法是否能够用于密码学和安全领域取决于是否具有不可预测性.

PGP密码软件

PGP其实是一款名为Pretty Good Privary的软件,具有以下功能

• 对称密码
• 公钥密码
• 数字签名
• 单向散列函数
• 证书
• 其他(压缩,钥匙串管理等)

信任网

在前面提到验证公钥合法性,即确认公钥来自正确的人没有被替换掉时,用到的时数字证书,再PGP中采用的则是信任网,PGP网络中会互相对对方的公钥进行数字签名,不依赖于认证机构,建立每个人之间的信任网络.

参考资料

[1] 图解密码技术(第三版)