DIFFPOOL（Hierarchical Graph Representation）

Differentiable Pooling)

论文链接：https://arxiv.org/pdf/1806.08804.pdf
https://mp.weixin.qq.com/s/-UqEQMFwCRgRt0FFDm4CpA
一些概念：置换矩阵：每个行以及每个列都只有一个1的矩阵，其可以看做是单位阵经过行的交换而生成的。置换阵一定是正交阵。左乘一个置换阵相当于是对矩阵进行了多次初等行变换，右乘一个置换阵相当于对矩阵进行了多次初等列变换。

这篇论文其实是属于子图嵌入这一类的，一般做子图嵌入的是直接把初始节点的特征简单的加起来当成是一个节点来用，或者是加上一个虚拟节点，直接放进网路里边跑，而这里采用的不一样的想法，将其子图集群起来。
该文提出了一个用于图（graph）分类的可微池化操作模块——DIFFPOOL，可以生成图的层级表示并且可以以端到端的方式被各种图神经网络整合。

动机

现在的GNN方法本质上来说都是平面的，没有学习到图的层次表示。这对于图形分类任务来说尤其成问题，因为其目标是预测与整个图形相关的标签。所以文章提出了 DIFFPOOL，一种可以产生图的分层表示以及可以将不同的图神经网络框架合并起来的端到端模型。DIFFPOOL在深度GNN中为每一层的节点学习可微分的软集群分配，将节点映射到一组集群，然后这些集群形成下一个GNN层的粗化输入。

核心思想

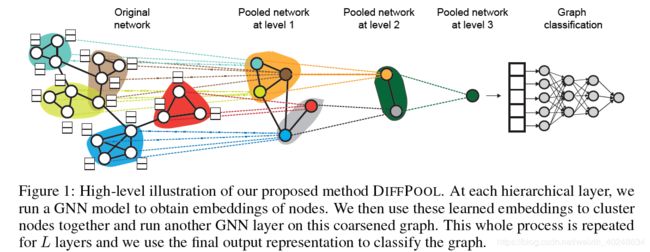
DIFFPOOL的核心思想是它能够通过一个微分模块去分层的聚合图节点，进而构造深的、多层的GNN模型。DIFFPOOL基于学习到的嵌入，将节点映射为簇（cluster）的集合，进而在GNN的每一层学习一个可微的软分配（soft assignment）。通过使用分层的方式将$l-1$层的簇输出（其实就是一个新的粗图而已），用于另一个GNN网络的输入，堆叠多个不同的GNN 层后，就可以建立深度 GNN，GNN 模块中 l 层的输入节点为l-1 层学到的簇（cluster）。
给定一个标签图的集合$D=（G_1，y_1），（G_2，y_2），...$，其中$y_i\in Y$是对应于$G_i\in G$的标签，图分类的目标是学习一个映射函数f：

$$f：G\to Y$$将图映射为标签的集合
其中：

• 图G表示为（A,F）
• $A\in {0,1}^{n\times n}$是邻接矩阵
• $F\in R^{n\times d}$是节点的特征矩阵
• d为每个节点的特征数

图神经网络

图分类的常规框架：
$$H^{(k)}=M(A,H^{(k-1)};{\theta }^{(k)})$$
其中：

• $H^{(k)}\in R^{n\times d}$,表示在GNN的k步之后计算得到的节点嵌入
• M是信息传播函数
• ${\Theta }^{(k)}$是可训练参数
• $H^{(0)}=F$,是图上的节点特征
  传播函数M有多种形式，使用图卷积神经网络GCN时，可以表示为：
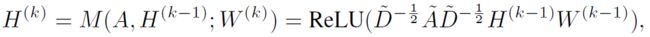  其中：
• $\tilde{A}=A+I$
• $\tilde{D}$为度矩阵
• W^(k)∈R{d×d}是可训练的权重矩阵
  一个GNN模块迭代K次，可以生成最终输出节点嵌入:
  $$Z=H^{(k)}\in {\mathbb{R}}^{n\times d}$$
  进而可以将任意GNN的内部结构抽象表示为：
  $$Z=GNN(A,X)$$

下面提出的可微分池化模型可以应用任何GNN模型来实现

可微分池化层

可微分池化层（DIFFPOOL层基于GNN第$l-1$层生成的节点嵌入X以及分配矩阵S，以端到端的方式将节点分配给第l层的簇，然后这些簇输入到 GNN 下一层，进而实现了用分层的方式堆叠多个GNN 层的想法，主要包含分配矩阵的学习以及池化分配矩阵两部分内容。

分配矩阵的学习

文中使用两个分开的GNN来生成分配矩阵$S^{(l)}$与每一个簇节点新的嵌入$Z^{(l)}$，这两个GNN都使用簇节点特征$X^{（l）}$与粗化邻接矩阵$A^{(l)}$作为输入。
通过嵌入GNN（可以选择任意的GNN框架）去生成每个簇节点在$l$层的新嵌入$Z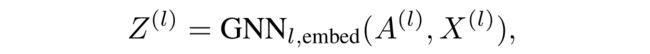^{(l)}$
$l$层的分配矩阵，这里使用的是池化GCN（可以选择任意的GNN框架）。这里$S^{(l)}$提供每个节点的下一个粗化$l+1$层中的簇的软分配（soft assignment）。
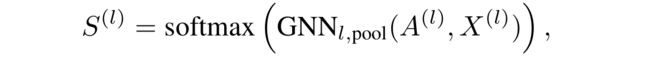其中：

• $S^{(l)}$的每一行对应于在l层的$n_l$个节点中的一个，$S^{(l)}$的每列对应于下一层l + 1处的$n_{l+1}$个簇中的一个

• softmax函数是以逐行的方式应用的。

• $GN{N}_{l,pool}$的输出维度为层l中的预先定义的最大簇数目。

• 第0层的输入为原始图的输入邻接矩阵A与节点特征F

• 在倒数第二层L-1处，需要将分配矩阵$S^{(L-1)}$设置为1维的向量，即最终层L处的所有节点被分配给单个簇，从而生成对应于整个图的最终嵌入向量

这两个GNN使用相同的输入数据，但使用不同的参数，并扮演不同的角色：嵌入GNN为此层的输入节点生成新的嵌入，而池化GNN生成输入节点下一层$n_{l+1}$簇的概率分配。

池化分配矩阵

通过GNN得到的分配矩阵$S^{(l)}$，与该层节点的新嵌入矩阵$Z^{(l)}$后，DIFFPOOL 层通过下式粗化输入图，对于图中的每个节点/簇生成一个新的粗化的邻接矩阵$A^{(l)}$与新的嵌入矩阵$X^{(l)}$,进而形成新的更加粗化的图：
其中：

• $A_{ij}^{(l+1)}$表示簇i和簇j之间的连接强度
• $X^{(l+1)}$的第i行对应于簇i的嵌入
  粗化的邻接矩阵$A_{ij}^{(l+1)}$和簇嵌入$X^{(l+1)}$合在一起可以用作另一个GNN层的输入。在新的粗化图中的每一个簇节点（图1中第一个池化网络中蓝色的节点）对应于图的 第 l 层的一个节点簇（图1原始图中蓝色的圈）。

优化

由于存在非凸优化问题，并且在训练早期使池化GNN远离虚假局部最小值是很困难的。因此，在图分类任务中不能仅仅使用梯度信号去训练池化GNN。文中使用辅助连接预测目标（Auxiliary Link Prediction Objective）来训练池化GNN，在每一个l层，最小化下面损失函数
$$L_{LP}=||A^{(l)},S^{(l)}{S}^{(l{)}^T}|{|}_F$$
其中：
‖ . ‖_F 表示Frobenius范数

one hot矩阵优化

并且对于每一个节点输出的簇分配应该接近于one-hot向量，以便明确定义每个簇或子图之间的关系。因此，文中还定义了最小化L_E损失来规范簇assignment的熵：
$$L_E=\frac{1}{n}\sum _{i=1}^{n}H(S_i)$$
其中：

• H表示熵函数
• S_i是S的第i行
  在训练期间，每层的$L_{LP}$和$L_E$ 被加入到分类损失中。

实验

数据集

文中使用了多种图分类基准数据，如蛋白质数据集（ENZYMES，PROTEINS，D&D），社交网络数据集（REDDIT-MULTI-12K），科研合作数据集（COLLAB）。其中10%的数据作为验证集，进行交叉验证以评估模型结果。

实验设置

在实验中，使用GRAPHSAGE架构作为DIFFPOOL的GNN模型，每两个GRAPHSAGE层之后应用DIFFPOOL层，嵌入矩阵和分配矩阵分别由两个单独的GRAPHSAGE模型。

Baseline

• 基于CNN的方法：

• 带有全局平均池化的 GRAPHSAGE。

• STRUCTURE2VEC（S2V），使用全局平均池化，该算法将潜在变量模型和 GNN 结合在一起。

• ECC：在CNN 中用于图形的边缘条件过滤器，使用图形粗化算法进行池化操作，将边缘信息整合到 GCN 模型中。

• PATCHYSAN：为每个节点定义了接受域（邻域），并使用了规范节点排序，对节点嵌入的线性序列应用卷积操作。

• SET2SET ：通过聚合替代了传统 GNN 架构的全局平均池化。

• SORTPOOL：应用 GNN 结构在排好序的节点嵌入上做了单层软池化，然后进行1D 卷积。

• DIFFPOOL-DET，是一种DIFFPOOL变体，使用确定性图聚类算法生成分配矩阵。

• DIFFPOOL-NOLP是DIFFPOOL的变体，取消了连接预测目标部分。

基于核的方法中，对于每个内核，计算归一化的gram矩阵，具体采用如下几个方法:

• GRAPHLET

• SHORTEST-PATH

• I-WL

• WLOA

实验结果

为了评估DIFFPOOL对一些最先进的图分类方法的影响，作者在基于 GNN 和现有最好的基于核的方法上进行验证。实验结果如下：
从上图可以观察到DIFFPOOL方法在GNN的所有池化方法中获得最高的平均性能。
为了更好地证明DIFFPOOL对于图分类十分有效，文中还使用了其他GNN体系结构（Structure2Vec（S2V）），并且构造了两个变体，进行对比实验：

• S2V WITH 1 DIFFPOOL：在S2V的第一层之后应用一个DIFFPOOL层，并且在DIFFPOOL的输出之上堆叠另外两个S2V层
• S2V WITH 2 DIFFPOOL：分别在S2V的第一层和第二层之后应用一个DIFFPOOL层
  结果： 从表中可以观察到DIFFPOOL显着改善了S2V在ENZYMES和D＆D数据集上的性能。
  除上述两个对比实验之外，文中还通过可视化不同层中的簇assignment研究DIFFPOOL学习有意义的节点簇的程度。图2显示了COLLAB数据集图中第一层和第二层中节点分配的可视化，其中节点颜色表示其簇的成员。节点簇成员是通过获取其簇assignment概率的最大参数值来确定的。
  

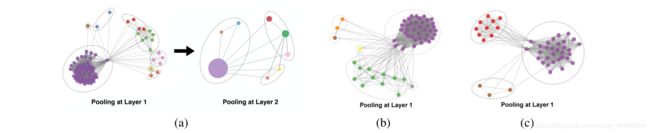
可以观察到即使在仅基于图形分类目标（即没有辅助连接预测目标）学习聚类分配时，DIFFPOOL仍然可以捕获层级结构。并且DIFFPOOL学会以非均匀的方式将节点转换为成软簇，并且倾向于将密集连接的子图转换成簇。

不足点

这个分配矩阵需要很多空间去存储，需要O(kV^2)存储复杂度，k为池化层的层数，所以对于大图来说这个收到很大的限制。