HDU 4832 Chess （DP）

Chess

Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 24    Accepted Submission(s): 10

Problem Description

　　小度和小良最近又迷上了下棋。棋盘一共有N行M列，我们可以把左上角的格子定为(1,1)，右下角的格子定为(N,M)。在他们的规则中，“王”在棋盘上的走法遵循十字路线。也就是说，如果“王”当前在(x,y)点，小度在下一步可以移动到(x+1, y), (x-1, y), (x, y+1), (x, y-1), (x+2, y), (x-2, y), (x, y+2), (x, y-2) 这八个点中的任意一个。


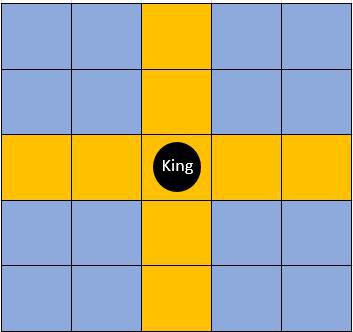
　　 图1 黄色部分为棋子所控制的范围
　　小度觉得每次都是小良赢，没意思。为了难倒小良，他想出了这样一个问题：如果一开始“王”在(x ₀,y ₀)点，小良对“王”连续移动恰好K步，一共可以有多少种不同的移动方案？两种方案相同，当且仅当它们的K次移动全部都是一样的。也就是说，先向左再向右移动，和先向右再向左移动被认为是不同的方案。
　　小良被难倒了。你能写程序解决这个问题吗？

 

 

Input

输入包括多组数据。输入数据的第一行是一个整数T(T≤10)，表示测试数据的组数。
每组测试数据只包括一行，为五个整数N,M,K,x ₀,y ₀。(1≤N,M,K≤1000,1≤x ₀≤N,1≤y ₀≤M)

 

 

Output

对于第k组数据，第一行输出Case #k:，第二行输出所求的方案数。由于答案可能非常大，你只需要输出结果对9999991取模之后的值即可。

 

 

Sample Input

2 2 2 1 1 1 2 2 2 1 1

 

 

Sample Output

Case #1: 2 Case #2: 4

 

 

Source

2014年百度之星程序设计大赛 - 初赛（第二轮）

 

 

 

可以很容易发现行和列是独立的。

 

只要做两个一维的DP。

 

然后组合起来就是答案了。

 

  1 /* ***********************************************

  2 Author        :kuangbin

  3 Created Time  :2014/5/25 14:57:15

  4 File Name     :E:\2014ACM\比赛\百度之星初赛2\B.cpp

  5 ************************************************ */

  6 

  7 #include <stdio.h>

  8 #include <string.h>

  9 #include <iostream>

 10 #include <algorithm>

 11 #include <vector>

 12 #include <queue>

 13 #include <set>

 14 #include <map>

 15 #include <string>

 16 #include <math.h>

 17 #include <stdlib.h>

 18 #include <time.h>

 19 using namespace std;

 20 

 21 const int MOD = 9999991;

 22 int C[1010][1010];

 23 int dp1[2020][1010];

 24 int dp2[2020][1010];

 25 int x,y;

 26 int n,m;

 27 int k;

 28 void add(int &a,int b)

 29 {

 30     a += b;

 31     if(a >= MOD)a -= MOD;

 32 }

 33 int sum1[1010];

 34 int sum2[1010];

 35 void init()

 36 {

 37     C[0][0] = 1;

 38     for(int i = 1;i < 1010;i++)

 39     {

 40         C[i][0] = C[i][i] = 1;

 41         for(int j = 1; j < i;j++)

 42         {

 43             C[i][j] = C[i-1][j] + C[i-1][j-1];

 44             if(C[i][j] >= MOD)

 45                 C[i][j] -= MOD;

 46         }

 47     }

 48     memset(dp1,0,sizeof(dp1));

 49     memset(dp2,0,sizeof(dp2));

 50     dp1[y][0] = 1;

 51     for(int t = 1;t <= k;t++)

 52         for(int i = 1;i <= m;i++)

 53         {

 54             dp1[i][t] = 0;

 55             if(i-2 >= 1)

 56             {

 57                 add(dp1[i][t],dp1[i-2][t-1]);

 58             }

 59             if(i - 1 >= 1)

 60             {

 61                 add(dp1[i][t],dp1[i-1][t-1]);

 62             }

 63             if(i + 1 <= m)

 64             {

 65                 add(dp1[i][t],dp1[i+1][t-1]);

 66             }

 67             if(i+2 <= m)

 68             {

 69                 add(dp1[i][t],dp1[i+2][t-1]);

 70             }

 71         }

 72     dp2[x][0] = 1;

 73     for(int t = 1;t <= k;t++)

 74         for(int i = 1;i <= n;i++)

 75         {

 76             dp2[i][t] = 0;

 77             if(i-2 >= 1)

 78             {

 79                 add(dp2[i][t],dp2[i-2][t-1]);

 80             }

 81             if(i - 1 >= 1)

 82             {

 83                 add(dp2[i][t],dp2[i-1][t-1]);

 84             }

 85             if(i + 1 <= n)

 86             {

 87                 add(dp2[i][t],dp2[i+1][t-1]);

 88             }

 89             if(i+2 <= n)

 90             {

 91                 add(dp2[i][t],dp2[i+2][t-1]);

 92             }

 93         }

 94     memset(sum1,0,sizeof(sum1));

 95     for(int i = 0;i <= k;i++)

 96         for(int j = 1;j <= m;j++)

 97             add(sum1[i],dp1[j][i]);

 98     memset(sum2,0,sizeof(sum2));

 99     for(int i = 0;i <= k;i++)

100         for(int j = 1;j <= n;j++)

101             add(sum2[i],dp2[j][i]);

102 }

103 

104 int main()

105 {

106     //freopen("in.txt","r",stdin);

107     //freopen("out.txt","w",stdout);

108     int T;

109     int iCase = 0;

110     scanf("%d",&T);

111     while(T--)

112     {

113         iCase++;

114         printf("Case #%d:\n",iCase);

115         scanf("%d%d%d%d%d",&n,&m,&k,&x,&y);

116         init();

117         long long ans = 0;

118         for(int i = 0;i <= k;i++)

119         {

120             ans += (long long)C[k][i] * sum1[i]%MOD*sum2[k-i]%MOD;

121             ans %= MOD;

122         }

123         printf("%d\n",(int)ans);

124 

125     }

126     return 0;

127 }