Understanding Batch Normalization
Batch Normalization
批标准化(Batch Normalization)输入为 mini-batch的数据,记为 I b , c , x , y I_{b,c,x,y} Ib,c,x,y. 输出也是维度为4的张量,记为 O b , c , x , y O_{b,c,x,y} Ob,c,x,y
其中,b表示batch,c为通道数, (x,y)是空间维度
算法:
输入: 一个mini-batch的数据 I b , c , x , y I_{b,c,x,y} Ib,c,x,y
要学习的参数: γ c , β c \gamma_c \;,\; \beta_c γc,βc
输出: O b , c , x , y O_{b,c,x,y} Ob,c,x,y
- 对每个通道,计算mini-batch的均值:
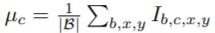
- 对每个通道,计算mini-batch的方差: σ c = 1 ∣ B ∣ ∑ b , x , y ( I b , c , x , y − μ c ) 2 \sigma_c=\frac{1}{\vert \mathcal{B} \vert} \sum_{b,x,y}(I_{b,c,x,y}-\mu_c)^2 σc=∣B∣1∑b,x,y(Ib,c,x,y−μc)2
- 标准化: I ^ b , c , x , y = I b , c , x , y − μ c σ c 2 + ϵ \hat{I}_{b,c,x,y}=\frac{I_{b,c,x,y}-\mu_c}{\sqrt{\sigma_c^2+\epsilon}} I^b,c,x,y=σc2+ϵIb,c,x,y−μc
- 尺度变换: O b , c , x , y = γ c I ^ b , c , x , y + β c O_{b,c,x,y}=\gamma_c \hat{I}_{b,c,x,y}+\beta_c Ob,c,x,y=γcI^b,c,x,y+βc
训练的时候, μ c , σ c \mu_c,\sigma_c μc,σc由上述公式得到。测试时,使用训练时所有 μ c , σ c \mu_c,\sigma_c μc,σc的平均值。
实验
初始条件
- 分类网络:110 层Resnet
- 数据集:CIFAR10
- 优化算法:SGD with momentum and weight decay
- 数据处理:标准的数据增强和图片预处理
| lr | 用BN | 不用BN |
|---|---|---|
| 0.1 | 收敛(橙色) | 不收敛 |
| 0.003 | 收敛(蓝色) , epoch=1320 | 不收敛 |
| 0.0001 | 收敛 (绿色) | 收敛 (红色), epoch=2400 |
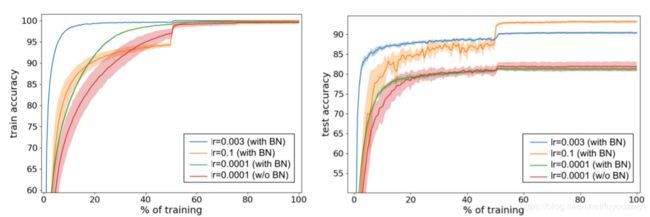
注,当lr降到0.0001时,不用BN的网络才能收敛。
批标准化后的网络:收敛更快(训练时间更短),正确率更高,能够使用更高的学习率
| lr | train accuracy | test accuracy |
|---|---|---|
| 0.003(with BN) | ≈ 100 | ≈90 |
| 0.1 (with BN) | ≈99.9 | ≈100 |
| 0.0001(with BN) | ≈99.8 | ≈80 |
| 0.0001(w/o BN) | ≈99.7 | ≈81 |
注:表中的数据是我根据作者的图估计的,并不严谨
从表中或图中可以看出,有BN的泛化性能更好
SGD
深度学习通常需要优化一个代价函数 l ( x ) l(x) l(x).
假设数据集一共有N个数据,则需要最小化经验风险
l ( x ) = 1 N ∑ i = 1 N l ( f ( x i ; w ) , y ) l(x)=\frac1N \sum_{i=1}^Nl(f(x_i;w),y) l(x)=N1i=1∑Nl(f(xi;w),y)
其中 f ( ⋅ ) f(\cdot) f(⋅)表示神经网络, w w w为参数.
按照最优化的理论,采用梯度下降法,求解最优解:
w n = w n − 1 − α ∇ l ( x ) , α ∇ l ( x ) = α 1 N ∇ w ∑ i = 1 N l ( f ( x i ; w ) , y i ) w_n=w_{n-1}-\alpha \nabla l(x) \;\;,\;\; \alpha\nabla l(x)=\alpha\frac1N \nabla_w \sum_{i=1}^Nl(f(x_i;w),y_i) wn=wn−1−α∇l(x),α∇l(x)=αN1∇wi=1∑Nl(f(xi;w),yi)
通常情况下,用于深度学习的数据集都过于庞大,如果每次更新梯度都需要遍历一遍数据集,就太慢了。
SGD则是随机选取一小部分数据,记为B,用这一小部分数据计算出的梯度,来估计整体的梯度。SGD算法中的梯度是对原本梯度的一种估计。
w n = w n − 1 − α ∇ S G D ( x ) , α ∇ S G D ( x ) = α ∣ B ∣ ∑ i ∇ w l i ( x ) w_n= w_{n-1}-\alpha\nabla_{SGD}(x)\;\;\;, \;\;\; \alpha\nabla_{SGD}(x)=\frac{\alpha}{|B|}\sum_i \nabla_wl_i(x) wn=wn−1−α∇SGD(x),α∇SGD(x)=∣B∣αi∑∇wli(x)
根据最优化理论,梯度应该取整个数据集梯度的均值,而SGD随机选取部分数据的梯度求均值,然后更新参数的值。所以这里存在一些噪声。我们定义噪声为
α ∇ S G D ( x ) − α ∇ l ( x ) = α ∣ B ∣ ∑ i ( ∇ l i ( x ) − ∇ l ( x ) ) \alpha\nabla_{SGD}(x)-\alpha\nabla l(x)=\frac{\alpha}{|B|}\sum_i (\nabla l_i(x)-\nabla l(x)) α∇SGD(x)−α∇l(x)=∣B∣αi∑(∇li(x)−∇l(x))
假如,有 E [ ∣ ∣ α ∇ S G D ( x ) − α ∇ l ( x ) ∣ ∣ 2 ] = 0 \mathbb{E}[||\alpha\nabla_{SGD}(x)-\alpha\nabla l(x)||^2]=0 E[∣∣α∇SGD(x)−α∇l(x)∣∣2]=0,则可以说是无偏估计,即随机梯度下降法和梯度下降法是等价的(在这个意义下)。但是总是存在一些噪声。根据推导有:
E [ ∣ ∣ α ∇ S G D ( x ) − α ∇ l ( x ) ∣ ∣ 2 ] ≤ α 2 ∣ B ∣ C \mathbb{E}[||\alpha\nabla_{SGD}(x)-\alpha\nabla l(x)||^2] \le \frac{\alpha^2}{|B|}C E[∣∣α∇SGD(x)−α∇l(x)∣∣2]≤∣B∣α2C
深度学习 — 优化入门五(Batch Normalization(批量归一化)
深度学习 — 优化入门五(Batch Normalization(批量归一化)二)
参考文献2