HDU-1133Buy the Ticket 卡特兰数买票问题

    题目：HDU-1133 Buy the Ticket

    题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1133

    题目：

Buy the Ticket

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 5746    Accepted Submission(s): 2391

Problem Description

The "Harry Potter and the Goblet of Fire" will be on show in the next few days. As a crazy fan of Harry Potter, you will go to the cinema and have the first sight, won’t you?

Suppose the cinema only has one ticket-office and the price for per-ticket is 50 dollars. The queue for buying the tickets is consisted of m + n persons (m persons each only has the 50-dollar bill and n persons each only has the 100-dollar bill).

Now the problem for you is to calculate the number of different ways of the queue that the buying process won't be stopped from the first person till the last person. 
Note: initially the ticket-office has no money. 

The buying process will be stopped on the occasion that the ticket-office has no 50-dollar bill but the first person of the queue only has the 100-dollar bill.

 

Input

The input file contains several test cases. Each test case is made up of two integer numbers: m and n. It is terminated by m = n = 0. Otherwise, m, n <=100.

 

Output

For each test case, first print the test number (counting from 1) in one line, then output the number of different ways in another line.

 

Sample Input

   
   
   
   

    
    
    
    3 0
3 1
3 3
0 0
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    Test #1:
6
Test #2:
18
Test #3:
180
   
   
   
   

 

    额，这道题我依旧是用Java做的，因为答案很长longlong也存不下，C++要么用数组存要么自己写一个大数据类，所以毫无疑问选择了Java，建议做ACM的同学如果没了解Java的话可以简单了解一下，至少大数据类用这还是挺方便的。

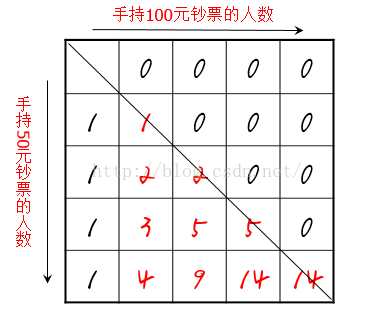
    题目分析，有n+m个人去买票，m个人拿50，n个人拿100，问有几种安排人排队的方法。明显是一个有关组合的问题，我们先判断一下特殊情况，只有在m>=n的情况下才可能安排排队，否则钱是找不开的，而且n=0时全是拿50的，那直接n的阶乘就好了。在一般情况下，可以列一个n*m的矩阵来表示答案，而且因为只要有几种排队方法确定以后直接乘以n的阶乘和m的阶乘就可以了，所以我们可以把n个人视为一样的，m个人视为一样的。那么就可以确定一般情况时排队方法有多少种。

    则第m+n个人的排队方式可以看做多了第m+n个人，本来已经有了(m+n-1)个人，如果这个人拿的是50，那么就是在（（m-1）+n）的基础上多了一个人，此时第m+n个人站在最后面（因为每个人都一样，所以实际上已经考虑了所有的情况），同样，如果这个人拿的是100，那么就是在（m+（n-1））的基础上多了一个人，因为人 都一样，所以又有（m，n-1）这种情况的种类，那么第m+n个人的排队类数就是（m，n-1）和（m-1，n）的和，（事实上如果最后来的那个人不站最后面那么就会出现重复的排队数，你可以试试用笔推一下）。那么递推式就出来了，我们就可以用打表的方法利用递推把m,n个人对应的排队数目用数组存储起来

    嗯哼，这个做法当然不是我想的，我要是有这么聪明就好了=-=。唉，我这令人担忧的智商。

    我们可以发现，对角线上的数字就是卡特兰数，也就是说如果m=n，那么排队数目就是卡特兰数 。

    之后求阶乘的步骤就不用再说，排队的种类数乘以m的阶乘和n的阶乘就去掉了我们之前把拿同一种钞票的人视为一样的做法的影响了，那么我们得到的就是最终答案了。小提示，求m和n的阶乘的时候即使是0的阶乘也要注意返回一个1，否则当n=0时计算结果就会出现错误~~

    啦啦啦，上代码~~

import java.util.*;
import java.math.*;
public class Main {
    public static void main(String[] args){
        Scanner input=new Scanner(System.in);
        BigInteger a=new BigInteger("1");
        BigInteger c=new BigInteger("0");
        BigInteger ans[][]=new BigInteger[105][105];
        for(int i=0;i<=100;i++)
            for(int j=0;j<=100;j++){
                if(i<j) ans[i][j]=c;
                else if(j==0) ans[i][j]=a;
                else{
                    ans[i][j]=ans[i][j-1].add(ans[i-1][j]);
                }
            }
        int count=0;
        while(true){
            int m=input.nextInt(),n=input.nextInt();
            if(m==0 && n==0) break;
            BigInteger e=new BigInteger("1");
            BigInteger f=new BigInteger("0");
            for(int i=1;i<=m;i++){
                f=f.add(a);
                e=e.multiply(f);
            }
            BigInteger g=new BigInteger("1");
            BigInteger h=new BigInteger("0");
            for(int i=1;i<=n;i++){
                h=h.add(a);
                g=g.multiply(h);
            }
            BigInteger b=ans[m][n].multiply(e).multiply(g);
            System.out.println("Test #"+ ++count+":");
            System.out.println(b);
        }
    }
}

    好好学习，天天向上，加油~~~