B树

　　常见的动态查找树有：二叉查找树（BST）、平衡二叉查找树（AVL）、红黑树（RB-Tree）、B-tree/B+-tree。
　　由于前面三种树都属于二叉树，因此树的高度为(log₂N)。树查找的时间复杂度与树的高度有关，因此要提高查找效率必须要降低树的高度，所以我们可以想到多叉树。
　　B树、B+树都是基于多叉树实现的。

磁盘读取

　　（参考http://blog.csdn.net/v_july_v/article/details/6530142）
　　由于内存是有限制的，一般最多也只有几个G。当存储数据量过大时，内存不再满足需求，此时必须用到辅存，如磁盘等。
　　虽然磁盘比主存便宜且容量大得多，但是它们的读写速度却很慢。一个典型的磁盘驱动器如下图所示：
　　
　　磁盘是一个扁平的圆盘。盘面上有许多称为磁道的圆圈，数据就记录在这些磁道上。
　　当磁盘驱动器执行读/写功能时。盘片装在一个主轴上，并绕主轴高速旋转，当磁道在读/写头(又叫磁头) 下通过时，就可以进行数据的读 / 写了，一个磁道对应一个柱面。

磁盘的读/写原理和效率

　　磁盘块是磁盘中数据存储、检索的基本单位。同一个磁盘具有固定大小的磁盘块，一般为512字节或4k字节。
　　磁盘上数据必须用一个三维地址唯一标示：柱面号、盘面号、块号(磁道上的盘块)
　　读/写磁盘上某一指定数据需要下面3个步骤：
　　(1) 首先移动臂根据柱面号使磁头移动到所需要的柱面上，这一过程被称为定位或查找
　　(2) 如上图所示，所有磁头都定位到了10个盘面的10条磁道上。这时根据盘面号来确定指定盘面上的磁道
　　(3) 盘面确定以后，盘片开始旋转，将指定块号的磁道段移动至磁头下
　　经过上面三个步骤，指定数据的存储位置就被找到。这时就可以开始读/写操作了。
　　
　　磁盘读取数据是以盘块(block)为基本单位的。位于同一盘块中的所有数据都能被一次性全部读取出来。而磁盘IO代价主要花费在查找时间上。因此我们应该尽量将相关信息存放在同一盘块，同一磁道中。或者至少放在同一柱面或相邻柱面上，以求在读/写信息时尽量减少磁头来回移动的次数，避免过多的查找时间。
　　
　　读写数据时，花费最大的是磁盘存取的时间。因此为了提高效率，我们必须降低磁盘查找存取的次数。因此想到了多叉树，如B树、B+树、B*树。本文将主要介绍B树的原理和操作。

B树

　　为了降低树的高度，B树的度一般都非常大。B树与红黑树的相似之处在于，每棵含n个节点的B树的高度为O(lgn)，但是可能比红黑树的高度小得多。
　　一棵简单的B树示意图如下：
　　
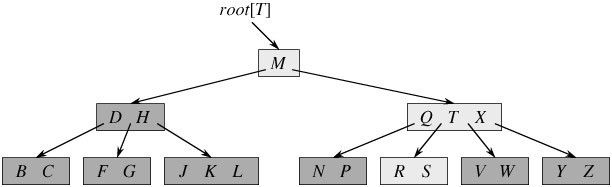
　　内节点：非叶子节点
　　如果B树的内节点x包含n[x]个关键字，则x节点就有n[x]+1个孩子节点。节点x中的n[x]个关键字将x所处理的关键字区间划分成n[x]+1个子区间。以根节点的左孩子节点为例，D、H两个关键字将该节点所处理的关键字区间划分成3个子区间：
　　1）key < D
　　2）D < key < H
　　3）key > D

B树的定义

　　B树必须满足：
　　1）每个节点x有以下域
　　　　a）n[x]，存储节点中的关键字数
　　　　b）key_i[x]，n[x]个关键字本身，以非降序方式存放，即key₁[x] ≤ key₂[x] ≤ …… ≤ key_n[x][x]
　　　　c）leaf[x]，为TRUE时，表明节点是叶子节点。否则为FALSE，表明节点为内节点
　　2）每个内节点还包含n[x]+1个指向其孩子的指针，c₁[x]、c₂[x]、……、c_n[x]+1[x]
　　3）每个内节点x中的n[x]个关键字对各子树中的关键字范围进行划分，n[x]个节点划分出n[x]+1个区间（子树）
　　4）每个叶节点具有相同的深度，即树的高度h
　　
　　5）除了上述的基本性质之外，还对B树的度有限制。若B树的最小度数为t ≥ 2，则
　　　　a）每个节点（根节点除外）必须至少有 t-1 个关键字，即至少有t个子树
　　　　b）每个节点最多有 2t-1 个关键字，即至少有2t个子树，此时节点是满的

　　t=2是最简单的B树，但是在实际应用中t的值要大得多。一般B树中的一个节点就占用磁盘中的一个块的内存（一般为512或4096字节）。由于在查找时，我们在B树的每一层最多访问一个节点，因此查找的时间复杂度为O(h)。而一个节点对应一个磁盘块，因此读取磁盘的次数也为O(h)。若B树的度为t，则B树的高度 h ≤ log_t((n+1)/2) ，比一般的二叉树读取磁盘的次数要少得多。
　　

B树的基本操作

　　数据结构的基本操作主要有：创建、查找、插入、删除　　

查找

　　查找首先在节点x中查找，若x节点中没有，则在x节点中目标所属范围的子树中查找　　

B-TREE-SEARCH(x,k)
{ i=1; while(i<=n[x] && k>key(x,i)){ ++i; }
    if(i<=n[x] && k==key(x,i)){ return (x,i); }
    if(leaf[x])
        return NULL;
    else{ DISK_READ(ci[x]); return B-TREE-SEARCH(ci[x],k); }
}

创建　　

　　创建一棵B树，可以首先创建一个空的根节点，然后依次插入所有元素。　　

B-TREE_CREATE(T) { x=allocate_node(); leaf[x]=true; n[x]=0; DISK_WRITE(x); root[T]=x; }

插入　 　　

　　由于对于度为t的B树，每个节点中关键字的数目必须为[t-1, 2t-1]中的一个值，因此当要插入的节点中已经有2t-1个节点时，就必须先对该节点进行分裂。
　　
　　分裂时以中间第t个关键字为轴将节点分裂成两个含有t-1个关键字的子树。然后将第t个节点提升到父节点中。示意图如下：
　　
　　有初始B树如下：
　　t=2，则每个节点的关键字数量必须为[t-1,2t-1]，即为[1,3]。因此当要插入的节点已经有3个关键字时，就必须进行分裂，以第t个即第二个关键字为中间轴进行分裂。
　　
　　当要插入关键字A时，最终会插入到y节点。而y节点已经有3个关键字，因此在插入之前必须先将y分裂成两个节点，并将H提升到父节点中
　　最终插入的结果为：
　　

　　　总结：
　　1）插入关键字最终都是插入到叶子节点中的
　　2）当要插入的节点已满时，必须先对其进行分裂，然后将中间关键字key_t[x]提升到父节点
　　3）当父节点已满时，必须先对父节点分裂，再提升关键字，一直向上递归
　　4）当根节点已满时，就需要创建一个新的根节点，用于保存原来根节点中的第t个关键字。此时树的高度会加1
　　可以发现，对根进行分裂是增加B树高度的唯一途径。B树高度的增加都是在根节点处发生的，下面所有的后代节点深度都会加1，因此所有叶子节点的深度都相同。
　　分裂的代码如下

B-TREE-SPLIT-CHILD(x,i,y)
{
    z=allocate_node();
    leaf[z]=leaf[y];
    n[z]=t-1;
    for(j=1;j<=t-1;++j){ //y中后半部分key拷贝到z中
        z[j]=y[t+j];
    }
    if(!leaf[y]){
        for(j=1;j<=t;++j){ //y中后半部分子树拷贝到z中
        c(z,j)=c(y,j+t);
    }
    n[y]=t-1;
    for(j=n[x]+1;j>i;--j){ //x中i之后是子树的指针后移1个
        c(x,j+1)=c(x,j);
    }
    c(x,i+1)=z;
    for(j=n[x];j>=i;--j){ //x中的key后移1位
        x[j+1]=x[j];
    }
    x[i]=y[t]; //y中中间节点提升到x中
    n[x]+=1;
    DISK_WRITE(x);
    DISK_WRITE(y);
    DISK_WRITE(z);

删除　　　

　　1）如果要删除的关键字在叶子节点上，且叶子节点关键字数大于t，则可以直接删除。
　　2）但如果在内节点中，由于每一个key左右都有一个子树，删除后会违背B树的定义，因此必须进行调整。
　　3）同时为了保证删除后每个节点至少有t-1个关键字，因此在查找过程中，保证递归的每个节点至少有t个关键字。否则就要先对节点进行合并，才能继续向下递归查找。
　　同样以t=2为例，则每个节点关键字数为[t-1,2t-1]，即为[1,3]
　　因此具体的删除可以分为三种情况：
　　1）要删除的关键字在叶子节点上，且叶子节点关键字数大于t，则可以直接删除
　　
　　2）要删除的key在内节点中
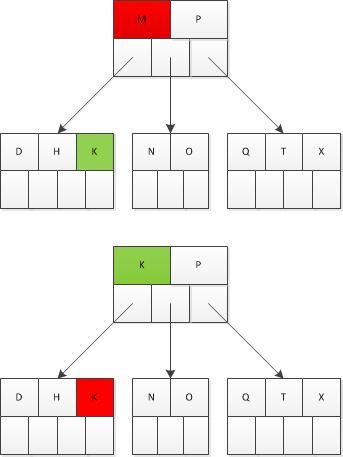
　　　　a）若节点x中浅语key的子节点中包含至少t个关键字，则找出key在以y节点为根节点的子树中的前驱k’，用k’替换k，并递归的删除k’。
　　　　如要删除M，而M的前驱为K，则用K替换M，并递归的删除K。
　　　　
　　　　b）相反，若y中关键字树小于t个，则看x位于key之后的子节点z中是否包含至少t个关键字。若是，则找出key的后继替换key，并递归删除。
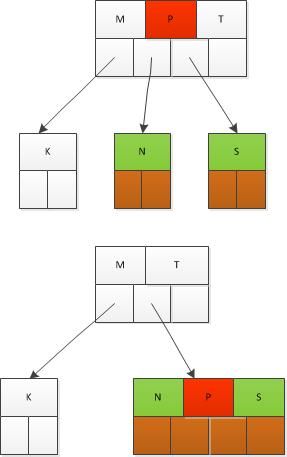
　　　　如要删除P，P之前的子节点只有一个关键字N，不满足2a。因此找到P的后继Q，用Q替换P，并递归的删除Q。
　　　　
　　　　c）若x中key前后子节点中关键字都少于t个，则将左右节点与key合并，然后再完成删除操作
　　　　如要删除P，y中只有一个关键字N，z中也只有一个关键字Q，因此首先将N、P、Q合并，然后删除P。
　　　　
　　3）如果要删除的key所在的节点x不是内节点，那么必须保证包含key的子树的根节点ci[x]至少包含t个关键字。如果ci[x]只包含t-1个关键字，则必须先完成下面的操作使得我们降至一个至少含有t个节点的子树。
　　　　a）如果ci[x]只包含t-1个关键字，但是它的一个相邻兄弟包含至少t个关键字。则将x中的一个关键字降至ci[x]，并将ci[x]的兄弟节点中的一个关键字提升到x中，这样ci[x]就有t个关键字了。然后再继续进行删除操作。
　　　　
　　　　b）如果ci[x]以及ci[x]的所有相邻兄弟都只包含t-1个关键字，则将ci[x]与一个兄弟节点合并，并将x中的一个关键字下降至合并后的节点，成为该节点中的中间关键字。
　　　　
　　

示例：

（http://cis.stvincent.edu/html/tutorials/swd/btree/btree.html）

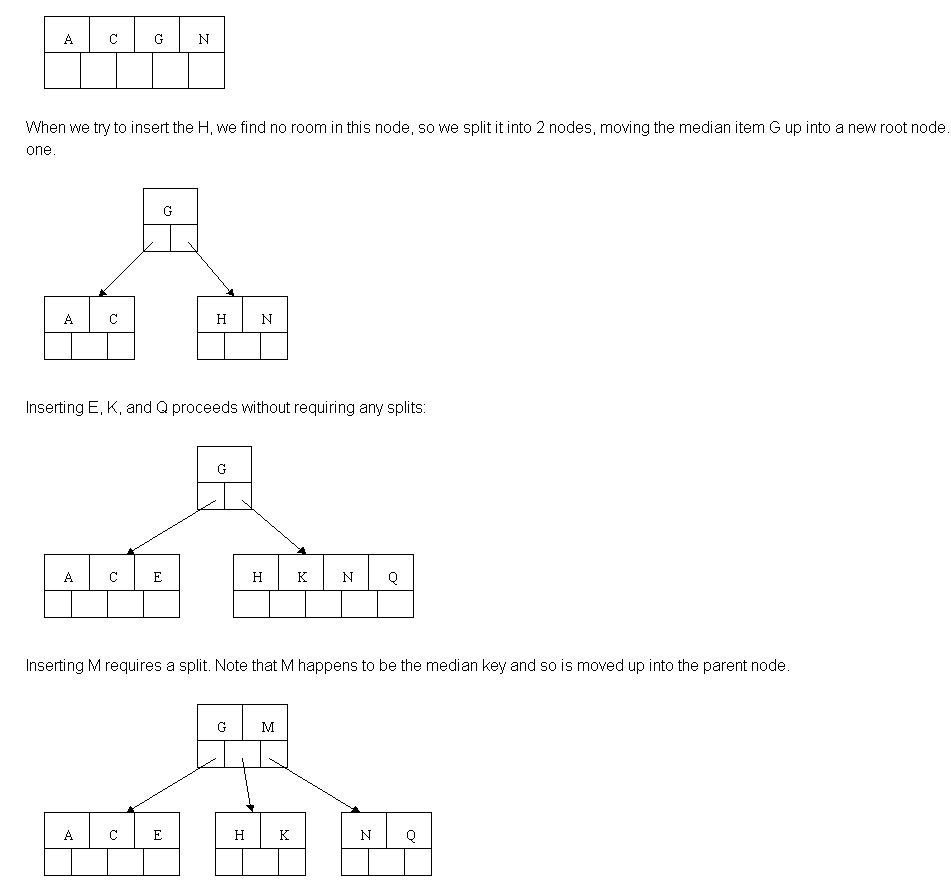
插入一个节点　

　　
　　
　　

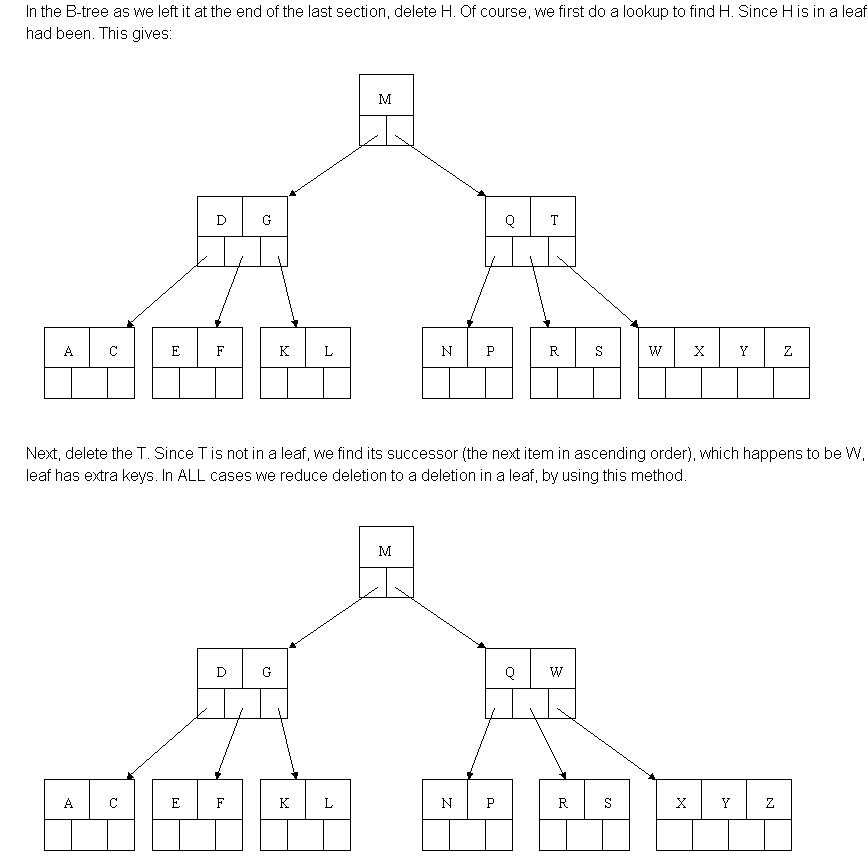
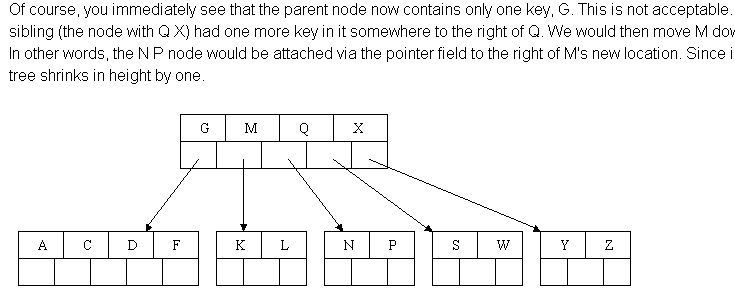
删除一个节点　

　　
　　
　　
　　

一个非常好的学习网站：http://cis.stvincent.edu/html/tutorials/swd/