单调队列、单调栈(第一周DIY)
Largest Rectangle in a Histogram
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Submission(s): 4087 Accepted Submission(s): 1218
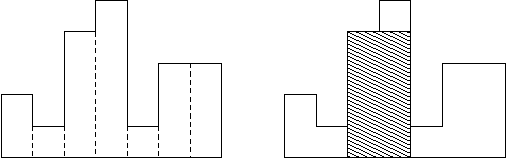
Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.
7 2 1 4 5 1 3 3 4 1000 1000 1000 1000 0
8 4000
http://acm.hdu.edu.cn/showproblem.php?pid=1506
方法一:
思路:对于每一点(设高度为h),向左找到第一个比它小的数(设这个下标为i),向右找到第一个比它小的数(设这个下标为j),那么此时以这点为高度的最大
面积为area=(i-j+1)*h; 以此类推,用for循环遍历数组,对每一点求面积,可求出最大的area.
关键:解题重点在于求左边和右边的“边界”,如果按常规算法,肯定会TLE,因此需用到动态规划。
#include<iostream>
#include<cstdio>
#include<stack>
using namespace std;
#define MAXN 100010
__int64 rec[MAXN], l[MAXN],r[MAXN],max_area,sum;
int main()
{
freopen("input.txt","r",stdin);
int n,i;
while(scanf("%d",&n),n){
for(i=1; i<=n; ++i){
scanf("%I64d",&rec[i]);
l[i]=r[i]=i;
}
rec[0]=rec[n+1]=-1;
for(i=1; i<=n; ++i){
while(rec[i] <= rec[l[i]-1])
l[i] = l[l[i]-1];
}
for(i=n; i>=1; --i){
while(rec[i] <= rec[r[i]+1])
r[i] = r[r[i]+1];
}
max_area = -2147483647;
for(i=1; i<=n; ++i){
sum = rec[i]*(r[i]-l[i]+1);
if(sum > max_area)
max_area = sum;
}
printf("%I64d\n",max_area);
}
return 0;
}
方法二(单调栈):
使用栈线性扫描解决该问题
对于一个新的元素:
(1)如果此时栈为空或者栈顶元素比新元素小,则将该元素入栈;
(2)如果栈顶元素与新元素相等,则跳过新元素;
(3)如果栈顶元素比新元素大,那么此时需要更新栈顶元素并更新面积,一直到栈顶元素小于新元素为止。
#include<iostream>
#include<cstdio>
#include<stack>
using namespace std;
__int64 rec[100010], max_area,sum;
int main()
{
//freopen("input.txt","r",stdin);
int n,i,temp;
while(scanf("%d",&n),n){
for(i=0; i<n; ++i)
scanf("%I64d",&rec[i]);
max_area = -2147483647; //注意: 不能给__int64或long long直接赋值-2147483648,否则会变成2147483648. 为什么?
rec[n]=-1; //最后一个元素的下一个赋值为-1, 则这个一定会比栈顶元素小
stack<int>q;
for(i=0; i<=n; ++i){
if(q.empty() || rec[i]>rec[q.top()]){
q.push(i);
}
else if(rec[i]<rec[q.top()]){
while(!q.empty() && rec[q.top()]>rec[i]){
sum = (i-q.top())*rec[q.top()];
if(sum>max_area)
max_area = sum;
temp = q.top(); //记录跳出盏的元素的下标。
q.pop();
}
q.push(temp); //此时temp下标表示以rec[i]为高度的矩形的左边的边界(因为盏是递减的,所以左边的比右边的高)
rec[temp] = rec[i]; //这里注意理解,把rec[i]的值赋值给rec[temp](原来的高度已经没用了),此时它表示的是高为rec[i]的矩形
}
}
printf("%I64d\n",max_area);
}
return 0;
}
Max Sum of Max-K-sub-sequence
Time Limit : 2000/1000ms (Java/Other) Memory Limit : 32768/32768K (Java/Other)
Total Submission(s) : 46 Accepted Submission(s) : 4
Now your job is to calculate the max sum of a Max-K-sub-sequence. Max-K-sub-sequence means a continuous non-empty sub-sequence which length not exceed K.
Then T lines follow, each line starts with two integers N , K(1<=N<=100000 , 1<=K<=N), then N integers followed(all the integers are between -1000 and 1000).
4 6 3 6 -1 2 -6 5 -5 6 4 6 -1 2 -6 5 -5 6 3 -1 2 -6 5 -5 6 6 6 -1 -1 -1 -1 -1 -1
7 1 3 7 1 3 7 6 2 -1 1 1
分析:因为序列是环状的,所以可以在序列后面复制一段(或者复制前k个数字)。如果用s[i]来表示复制过后的序列的前i个数的和,那么任意一个子序列[i..j]的和就等于s[j]-s[i-1]。对于每一个j,用s[j]减去最小的一个s[i](i>=j-k+1)就可以得到以j为终点长度不大于k的和最大的序列了。将原问题转化为这样一个问题后,就可以用单调队列解决了。
单调队列即保持队列中的元素单调递增(或递减)的这样一个队列,可以从两头删除,只能从队尾插入。单调队列的具体作用在于,由于保持队列中的元素满足单调性,对于上述问题中的每个j,可以用O(1)的时间找到对应的s[i]。(保持队列中的元素单调增的话,队首元素便是所要的元素了)。
维护方法:对于每个j,我们插入s[j-1](为什么不是s[j]? 队列里面维护的是区间开始的下标,j是区间结束的下标),插入时从队尾插入。为了保证队列的单调性,我们从队尾开始删除元素,直到队尾元素比当前需要插入的元素优(本题中是值比待插入元素小,位置比待插入元素靠前,不过后面这一个条件可以不考虑),就将当前元素插入到队尾。之所以可以将之前的队列尾部元素全部删除,是因为它们已经不可能成为最优的元素了,因为当前要插入的元素位置比它们靠前,值比它们小。我们要找的,是满足(i>=j-k+1)的i中最小的s[i],位置越大越可能成为后面的j的最优s[i]。
在插入元素后,从队首开始,将不符合限制条件(i>=j-k+1)的元素全部删除,此时队列一定不为空。(因为刚刚插入了一个一定符合条件的元素)
#include<iostream>
#include<cstdio>
#include<deque>
using namespace std;
int arr[200010],sum[200010];
int main()
{
// freopen("input.txt","r",stdin);
int T;
int N,K,i;
scanf("%d",&T);
while(T--){
scanf("%d %d",&N,&K);
sum[0] = 0;
for(i=1; i<=N; ++i){
scanf("%d",&arr[i]);
sum[i] = sum[i-1] + arr[i];
}
for(i=N+1; i<N+K; ++i){
sum[i] = sum[i-1] + arr[i-N];
}
deque<int>q;
q.clear();
int max = -2147483647,start,end;
for(i=1; i<N+K; ++i){
while(!q.empty() && sum[q.back()] > sum[i-1])
q.pop_back ();
while(!q.empty() && q.front() < (i-K))
q.pop_front();
q.push_back (i-1);
int val = sum[i] - sum[q.front()];
if(val > max){
max = val;
start = q.front() + 1;
end = i;
}
}
printf("%d %d %d\n",max, start, end>N?end%N:end);
}
return 0;
}
这一题中,用到了一个技巧,即对于一个序列 1,2,3,4,5,6,7,…… 要求某一区间的和, 例如第i数到第j个数的和,那么可以用前j个数的和减去前i-1个数的和
这个技巧可以拓展到矩阵,看下一题:
最大子矩阵
Time Limit : 30000/10000ms (Java/Other) Memory Limit : 32768/32768K (Java/Other)
Total Submission(s) : 7 Accepted Submission(s) : 4
1 4 5 2 2 3 361 649 676 588 992 762 156 993 169 662 34 638 89 543 525 165 254 809 280
2474
http://acm.hdu.edu.cn/showproblem.php?pid=1559
对于一个n行的矩阵,可以把n行看成一行,即和并列,每一列看成一个元素;以此推广。
#include<iostream>
#include<cstdio>
#include<deque>
using namespace std;
int arr[200010],sum[200010];
int main()
{
// freopen("input.txt","r",stdin);
int T;
int N,K,i;
scanf("%d",&T);
while(T--){
scanf("%d %d",&N,&K);
sum[0] = 0;
for(i=1; i<=N; ++i){
scanf("%d",&arr[i]);
sum[i] = sum[i-1] + arr[i];
}
for(i=N+1; i<N+K; ++i){
sum[i] = sum[i-1] + arr[i-N];
}
deque<int>q;
q.clear();
int max = -2147483647,start,end;
for(i=1; i<N+K; ++i){
while(!q.empty() && sum[q.back()] > sum[i-1])
q.pop_back ();
while(!q.empty() && q.front() < (i-K))
q.pop_front();
q.push_back (i-1);
int val = sum[i] - sum[q.front()];
if(val > max){
max = val;
start = q.front() + 1;
end = i;
}
}
printf("%d %d %d\n",max, start, end>N?end%N:end);
}
return 0;
}
—— 生命的意义,在于赋予它意义。