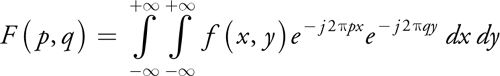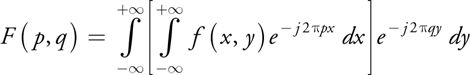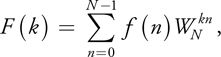1D傅里叶变换:

1D傅里叶逆变换:
2D傅里叶变换:
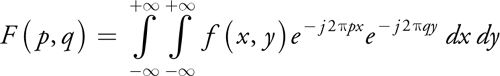
2D傅里叶变换通过两次1D傅里叶变换实现:
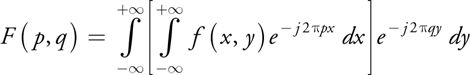
由此我们只需要关注1D的傅里叶变换如何处理,又因为我们处理图片的时候都是离散的点信息,最终我们得到的傅里叶变换是:
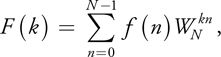
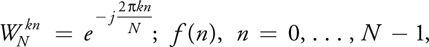
逆变换:

上述的傅里叶变换公式很直观,图像进行傅里叶变换时,像素点是n,最终转换到频域的时候,结果纹理存储的是k点的集合。(比较重要的是,傅里叶变换和逆变换不同点只有两个:(1/N)和(-kn),这说明他们的算法实现可以共用)
快速傅里叶算法(FFT):
先看一下一个8个采样点的快速傅里叶变换,它是基2,基4,基8的快速傅里叶算法的基础:
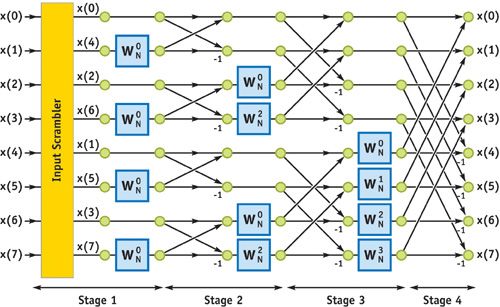
1.看下面不起眼的stage单词没,它对整个过程划分了几个阶段,个人感觉这里的划分有问题,应该是3个阶段。每个阶段有几个过程:(n个输入:log2(n+1)个阶段:nlog2(n)次复数乘法和加法)
(1)排序过程:黄颜色的部分,执行排序功能,让需要计算的两个值排在一起进行计算。
k = BIT_REVERSE(n)
(2)加权过程:蓝颜色部分,相乘的两个位置为奇数位的需要乘一个W(n0),看上面好像只有第1个阶段是对的,其实第2个和第3个阶段如果排完序就是对的了。
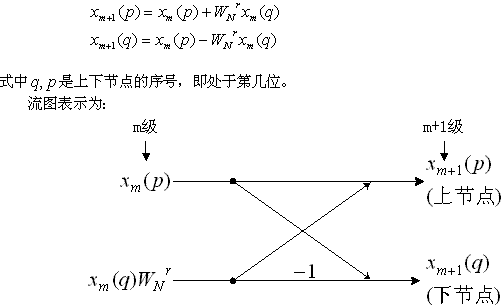
(3)蝶形算法过程:
一次蝶形运算:两次复数加法 + 两次复数乘法 (复数加法:2次浮点加法 复数乘法:4次浮点乘法+2次浮点加法) 一次蝶形运算 = 8次浮点乘 + 8次浮点加
FFT算法实现:
1.FFT:
// data为输入和输出的数据,N为长度
bool CFFT::Forward(complex *const Data, const unsigned int N)
{
if (!Data || N < 1 || N & (N - 1))
return false;
// 排序
Rearrange(Data, N);
// FFT计算:const bool Inverse = false
Perform(Data, N);
return true;
} 2.IFFT:
// Scale 为是否缩放
bool CFFT::Inverse(complex *const Data, const unsigned int N,
const bool Scale /* = true */)
{
if (!Data || N < 1 || N & (N - 1))
return false;
// 排序
Rearrange(Data, N);
// FFT计算,ture表示是逆运算
Perform(Data, N, true);
// 对结果进行缩放
if (Scale)
CFFT::Scale(Data, N);
return true;
}
3.排序:
void CFFT::Rearrange(complex *const Data, const unsigned int N)
{
// Swap position
unsigned int Target = 0;
// Process all positions of input signal
for (unsigned int Position = 0; Position < N; ++Position)
{
// Only for not yet swapped entries
if (Target > Position)
{
// Swap entries
const complex Temp(Data[Target]);
Data[Target] = Data[Position];
Data[Position] = Temp;
}
// Bit mask
unsigned int Mask = N;
// While bit is set
while (Target & (Mask >>= 1))
// Drop bit
Target &= ~Mask;
// The current bit is 0 - set it
Target |= Mask;
}
}
4.FFT计算:
void CFFT::Perform(complex *const Data, const unsigned int N,
const bool Inverse /* = false */)
{
const double pi = Inverse ? 3.14159265358979323846 : -3.14159265358979323846;
// Iteration through dyads, quadruples, octads and so on...
for (unsigned int Step = 1; Step < N; Step <<= 1)
{
// Jump to the next entry of the same transform factor
const unsigned int Jump = Step << 1;
// Angle increment
const double delta = pi / double(Step);
// Auxiliary sin(delta / 2)
const double Sine = sin(delta * .5);
// Multiplier for trigonometric recurrence
const complex Multiplier(-2. * Sine * Sine, sin(delta));
// Start value for transform factor, fi = 0
complex Factor(1.);
// Iteration through groups of different transform factor
for (unsigned int Group = 0; Group < Step; ++Group)
{
// Iteration within group
for (unsigned int Pair = Group; Pair < N; Pair += Jump)
{
// Match position
const unsigned int Match = Pair + Step;
// Second term of two-point transform
const complex Product(Factor * Data[Match]);
// Transform for fi + pi
Data[Match] = Data[Pair] - Product;
// Transform for fi
Data[Pair] += Product;
}
// Successive transform factor via trigonometric recurrence
Factor = Multiplier * Factor + Factor;
}
}
}
5.缩放:
void CFFT::Scale(complex *const Data, const unsigned int N)
{
const double Factor = 1. / double(N);
// Scale all data entries
for (unsigned int Position = 0; Position < N; ++Position)
Data[Position] *= Factor;
}
2D傅里叶变换:
2D的就是做两次1D的FFT运算
FFT对图片的处理:
FFT对图片的处理主要需要注意的是参数怎么控制,对于灰度图来说,灰度值是实数位,0为虚数为。对于RGB则是对RGB分别进行FFT转换,其中R,G,B分别为实数,虚数位依旧是0。
参考:
http://www.librow.com/articles/article-10