1. Hashing
-- Save items in a key-indexed table (index is a function of the key).
-- Hash function: Method for computing array index from key.
-- Classic space-time tradeoff.
-- No space limitation: trivial hash function with key as index.
-- No time limitation: trivial collision resolution with sequential search.
-- Space and time limitations: hashing (the real world).
2. Computing the hash function
-- Idealistic goal: scramble the keys uniformly to produce a table index.
-- Efficiently computable.
-- Each table index equally likely for each key.
-- Practical challenge. Need different approach for each key type.
3. Java hashCode implementation :
-- Integer :
public final class Integer
{
private final int value;
...
public int hashCode() {
return value; //using value of the Integer itself
}
}
-- Boolean :
public final class Boolean
{
private final boolean value;
...
public int hashCode() {
if (value) return 1231;
else return 1237;
}
}
-- Double :
public final class Double
{
private final double value;
...
public int hashCode() {
long bits = doubleToLongBits(value); //convert to IEEE 64-bit representation;
return (int) (bits ^ (bits >>> 32)); //xor most significant 32-bits with least significant 32-bits
}
}
-- String :
public final class String
{
private final char[] s;
...
public int hashCode() {
int hash = 0;
// Horner's method to hash string of length L: L multiplies/adds.
// Equivalent to h = s[0] · 31^(L–1) + … + s[L – 3] · 31^2 + s[L – 2] · 31^1 + s[L – 1] · 31^0.
for (int i = 0; i < length(); i++)
hash = s[i] + (31 * hash);
return hash;
}
}
-- user-defined types
public final class Transaction implements Comparable<Transaction>
{
private final String who;
private final Date when;
private final double amount;
...
public int hashCode() {
int hash = 17;
hash = 31*hash + who.hashCode();
hash = 31*hash + when.hashCode();
hash = 31*hash + ((Double) amount).hashCode();
return hash;
}
}
-- "Standard" recipe for user-defined types:
-- Combine each significant field using the 31x + y rule.
-- If field is a primitive type, use wrapper type hashCode().
-- If field is null, return 0.
-- If field is a reference type, use hashCode().
-- If field is an array, apply to each entry.
-- Modular hashing:
-- Hash code: An int between -2^31 and 2^31 - 1.
-- Hash function: An int between 0 and M - 1 (for use as array index).
-- Math.abs(key.hashCode()) % M --> 1-in-a-billion bug: hashCode() of "polygenelubricants" is -2^31
-- correct implementation:
private int hash(Key key) {
return (key.hashCode() & 0x7fffffff) % M;
}
4. Uniform hashing assumption:
-- Uniform hashing assumption: Each key is equally likely to hash to an integer between 0 and M - 1.
-- Birthday problem: Expect two balls in the same bin after ~ sqrt( π M / 2 ) tosses.
-- Coupon collector: Expect every bin has ≥ 1 ball after ~ M ln M tosses.
-- Load balancing: After M tosses, expect most loaded bin has Θ ( log M / log log M ) balls.
5. Separate chaining hash table
-- Use an array of M < N linked lists.
-- Hash: map key to integer i between 0 and M - 1.
-- Insert: put at front of ith chain (if not already there).
-- Search: need to search only ith chain.
-- Java Implementation
public class SeparateChainingHashST<Key, Value>
{
private int M = 97; // number of chains
private Node[] st = new Node[M]; // array of chains , array doubling and halving code omitted
private static class Node
{
private Object key;
private Object val;
private Node next;
}
private int hash(Key key) {
return (key.hashCode() & 0x7fffffff) % M;
}
public Value get(Key key) {
int i = hash(key);
for (Node x = st[i]; x != null; x = x.next)
if (key.equals(x.key)) return (Value) x.val;
return null;
}
public void put(Key key, Value val) {
int i = hash(key);
for (Node x = st[i]; x != null; x = x.next)
if (key.equals(x.key)) {
x.val = val; return;
}
st[i] = new Node(key, val, st[i]);
}
}
6. Analysis of separate chaining :
-- Proposition: Under uniform hashing assumption, prob. that the number of keys in a list is within a constant factor of N / M is extremely close to 1.
-- Consequence: Number of probes for search/insert is proportional to N / M.
-- M too large ⇒ too many empty chains.
-- M too small ⇒ chains too long.
-- Typical choice: M ~ N / 5 ⇒ constant-time ops.
7. Open addressing
-- When a new key collides, find next empty slot, and put it there.
-- Hash: Map key to integer i between 0 and M-1.
-- Insert: Put at table index i if free; if not try i+1, i+2, etc.
-- Search. Search table index i; if occupied but no match, try i+1, i+2, etc.
-- Array size M must be greater than number of key-value pairs N.
-- Java Implementation
public class LinearProbingHashST<Key, Value>
{
private int M = 30001;
private Value[] vals = (Value[]) new Object[M]; // array doubling and halving code omitted
private Key[] keys = (Key[]) new Object[M];
private int hash(Key key) { /* as before */ }
public void put(Key key, Value val) {
int i;
for (i = hash(key); keys[i] != null; i = (i+1) % M)
if (keys[i].equals(key))
break;
keys[i] = key;
vals[i] = val;
}
public Value get(Key key){
for (int i = hash(key); keys[i] != null; i = (i+1) % M)
if (key.equals(keys[i]))
return vals[i];
return null;
}
}
8. Knuth's parking problem
-- Model. Cars arrive at one-way street with M parking spaces. Each desires a random space i : if space i is taken, try i + 1, i + 2, etc. What is mean displacement of a car?
-- Half-full: With M / 2 cars, mean displacement is ~ 3 / 2.
-- Full: With M cars, mean displacement is ~ sqrt( π M / 8 ).
-- Proposition. Under uniform hashing assumption, the average # of probes in a linear probing hash table of size M that contains N = α M keys is: ~1/2(1+1/(1-α ) ) for search hit and ~1/2(1+1/(1-α )^2) for search miss or insert.
-- Parameter choice
-- M too large ⇒ too many empty array entries.
-- M too small ⇒ search time blows up.
-- Typical choice: α = N / M ~ ½.
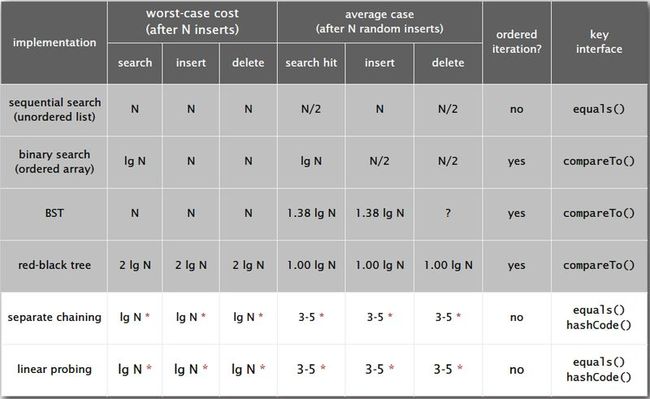
9. ST implementations summary:
10. Hashing Variations:
-- Two-probe hashing. (separate-chaining variant)
-- Hash to two positions, insert key in shorter of the two chains.
-- Reduces expected length of the longest chain to log log N.
-- Double hashing. (linear-probing variant)
-- Use linear probing, but skip a variable amount, not just 1 each time.
-- Effectively eliminates clustering.
-- Can allow table to become nearly full.
-- More difficult to implement delete.
-- Cuckoo hashing. (linear-probing variant)
-- Hash key to two positions; insert key into either position; if occupied, reinsert displaced key into its alternative position (and recur).
-- Constant worst case time for search.