1. For collections, which item to delete ?
Stack: Remove the item most recently added.
Queue: Remove the item least recently added.
Randomized queue: Remove a random item.
Priority queue: Remove the largest (or smallest) item.
2. Priority Queue interfaces:
MaxPQ(): create an empty priority queue
MaxPQ(Key[] a): create a priority queue with given keys
void insert(Key v): insert a key into the priority queue
Key delMax(): return and remove the largest key
boolean isEmpty(): is the priority queue empty?
Key max(): return the largest key
int size(): number of entries in the priority queue
3. Find the largest M items in a stream of N items:
| implementation | time | space |
| sort | N log N | N |
| elementary PQ | M N | M |
| binary heap | NlogM | M |
| best in theory | N | M |
4. unordered array implementation:
public class UnorderedMaxPQ<Key extends Comparable<Key>>
{
private Key[] pq; // pq[i] = ith element on pq
private int N; // number of elements on pq
public UnorderedMaxPQ(int capacity)
{ pq = (Key[]) new Comparable[capacity]; }
public boolean isEmpty()
{ return N == 0; }
public void insert(Key x)
{ pq[N++] = x; }
public Key delMax()
{
int max = 0;
for (int i = 1; i < N; i++)
if (less(max, i)) max = i;
exch(max, N-1);
Key result = pq[--N];
pq[N] = null;
return result;
}
}
5. order of growth of running time for priority queue with N items:
| implementation | insert | del max | max |
| unordered array | 1 | N | N |
| ordered array | N | 1 | 1 |
| goal | logN | logN | logN |
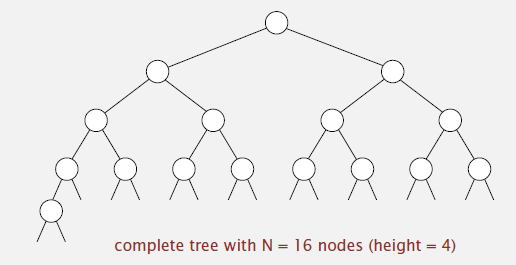
6. Binary tree: Empty or node with links to left and right binary trees.
Complete tree: Perfectly balanced, except for bottom level.
Property: Height of complete tree with N nodes is ⎣log N⎦.
7. Binary heap: Array representation of a heap-ordered complete binary tree.
Heap-ordered binary tree:
a) Keys in nodes.
b) Parent's key no smaller than children's keys.
Array representation:
a) Indices start at 1.
b) Take nodes in level order.
c) No explicit links needed!
8. Can use array indices to move through binary tree:
a) Largest key is a[1], which is root of binary tree.
b) Parent of node at k is at k/2.
c) Children of node at k are at 2k and 2k+1.
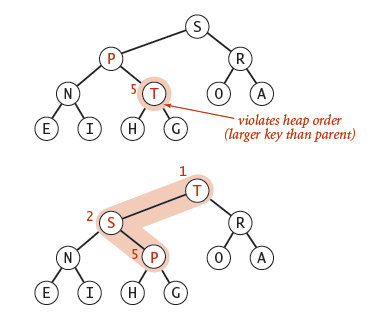
9. To eliminate the violation that child's key becomes larger key than its parent's key:
a) Exchange key in child with key in parent.
b) Repeat until heap order restored.
private void swim(int k)
{
while (k > 1 && less(k/2, k))
{
exch(k, k/2);
k = k/2;
}
}
10. Insertion in a heap: Add node at end, then swim it up:
public void insert(Key x)
{
pq[++N] = x;
swim(N);
}
Cost : At most 1 + lg N compares.
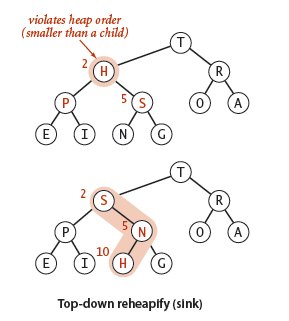
11. To eleminate the violation that parent's key becomes smaller than one (or both) of its children's:
a) Exchange key in parent with key in larger child.
b) Repeat until heap order restored.
private void sink(int k)
{
while (2*k <= N)
{
int j = 2*k;
if (j < N && less(j, j+1)) j++;
if (!less(k, j)) break;
exch(k, j);
k = j;
}
}
12. Delete the maximum in a heap: Exchange root with node at end, then sink it down:
public Key delMax()
{
Key max = pq[1];
exch(1, N--);
sink(1);
pq[N+1] = null;
return max;
}
Cost: At most 2 lg N compares.
13. Order-of-growth of running time for priority queue with N items:
| implementation | insert | del max | max |
| unordered array | 1 | N | N |
| ordered array | N | 1 | 1 |
| binary heap | log N | log N | 1 |
| d-ary heap | logd N | d logd N | 1 |
| Fibonacci | 1 | log N | 1 |
| impossibl | 1 | 1 | 1 |
14. Binary heap considerations:
Immutability of keys:
a) Assumption: client does not change keys while they're on the PQ.
b) Best practice: use immutable keys.
Underflow and overflow:
a) Underflow: throw exception if deleting from empty PQ.
b) Overflow: add no-arg constructor and use resizing array.
15. Immutable: String, Integer, Double, Color.
Mutable: StringBuilder, Stack, Java array.
16. Advantages of immutable type:
a) Simplifies debugging.
b) Safer in presence of hostile code.
c) Simplifies concurrent programming.
d) Safe to use as key in priority queue or symbol table.
Disadvantage: Must create new object for each data type value.
17. Basic plan for in-place heap sort.
a) Create max-heap with all N keys.
b) Repeatedly remove the maximum key.
18. Heap construction: Build heap using bottom-up method.
for (int k = N/2; k >= 1; k--) sink(a, k, N);
19. Java implementation of heap sort :
public class Heap
{
public static void sort(Comparable[] a)
{
int N = a.length;
for (int k = N/2; k >= 1; k--)
sink(a, k, N);
while (N > 1)
{
exch(a, 1, N);
sink(a, 1, --N);
}
}
private static void sink(Comparable[] a, int k, int N)
{ /* as before */ }
private static boolean less(Comparable[] a, int i, int j)
{ /* as before but convert from 1-based indexing to 0-base indexing*/ }
private static void exch(Comparable[] a, int i, int j)
{ /* as before but convert from 1-based indexing to 0-base indexing*/ }
}
20. Heap construction uses ≤ 2 N compares and exchanges.
Heapsort uses ≤ 2 N log N compares and exchanges.
Heapsort is optimal for both time and space, but:
a) Inner loop longer than quicksort’s.
b) Makes poor use of cache memory. (last item will exchange with first item)
c) Not stable.
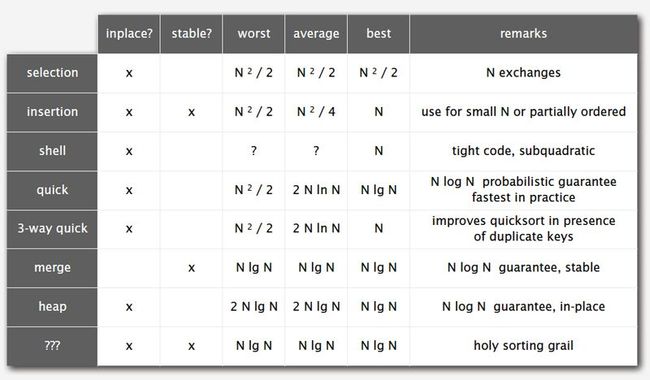
21. Sorting Algorithm Summary: