1. Sorted Arrays: Supported Operations
a) Search (binary search) θ(log(n))
b) Select (given order statistic i ) O(1)
c) MIN/MAX O(1)
d) Pred/Succ (given pointer/index to a key) O(1)
e) Rank (i.e., # of keys less than or equal to a given value) O(log(n))
f) Output in sorted order O(n)
g) insertion and deletion θ(n)
2. Balanced Search Trees: Supported Operations
a) Search θ(log(n))
b) Select O(log(n))
c) MIN/MAX O(log(n))
d) Pred/Succ O(log(n))
e) Rank O(log(n))
f) Output in sorted order O(n)
g) Insert/Delete O(log(n))
Like sorted array + fast (logarithmic) inserts + deletes !
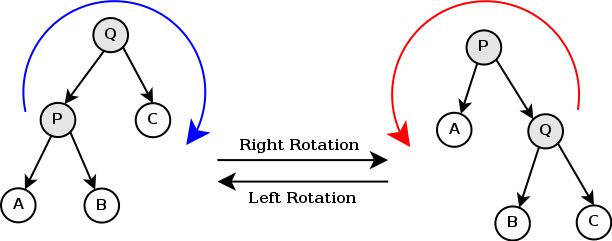
3. Binary Search Tree Structure
-- exactly one node per key
-- most basic version :
each node has
-- left child pointer
-- right child pointer
-- parent pointer
-- for an arbitrary node , it's bigger than any nodes in its left child tree and less than those in its right child tree.
Height of tree: longest root-leaf path
4. Min, Max, Pred, And Succ
To compute the minimum (maximum) key of a tree
- Start at root
- Follow left child (right child for maximum) untill you can't anymore
- return last key found
5. To compute the predecessor of key k
- Easy case : If k’s left subtree nonempty, return max key in left subtree
- Otherwise : follow parent pointers until you get to a key less than k.
6. n-Order Traversal
- Let r = root of search tree, with subtrees TL and TR
- recurse on TL
- Print out r’s key
- Recurse on TR
7. Deletion--To delete a key k from a search tree
-- Search for k
-- easy case : (k’s node has no children)
--Just delete k’s node from tree
-- mediaum case : (k’s node has one child)
--Unique child assumes position previously held by k’s node
-- difficult case : (k’s node has 2 children)
--Compute k’s predecessor i
-- Swap k and i (in it’s new position, k has no right child )
8. Select and Rank
Idea : store the size of the node at each node
size(x) = # of tree nodes in subtree rooted at x.
if x has children y and z, then size(y) + size(z) + 1
Easy to keep sizes up-to-date during an Insertion or Deletion
To select ith order statistic from augmented search tree (with subtree sizes)
-- start at root x, with children y and z
-- let a = size(y) [a = 0 if x has no left child ]
-- if a = i-1, return x’s key
-- if a >= i, recursively compute ith order statistic of search tree rooted at y
-- if a < i-1 recursively compute (i-a-1)th order statistic of search tree rooted at z
9. Balanced Search Trees :
Idea : ensure that height is always O(log(n)) [best possible]
Search / Insert / Delete / Min / Max / Pred / Succ will then run in O(log(n)) time [n = # of keys in tree]
10. Red-Black Tree Invariants
a) Each node red or black
b) Root is black
c) No 2 reds in a row [ red node => only black children ]
d) Every root-NULL path has same number of black nodes
11. Height Guarantee
Claim : every red-black tree with n nodes has height <= 2log2(n+1)
Proof : If every root-NUL path has >= k nodes, then tree includes (at the top) a perfectly balanced search tree of depth k-1. => Size n of the tree must be at least 2^k -1. => k <= log2(n+1)
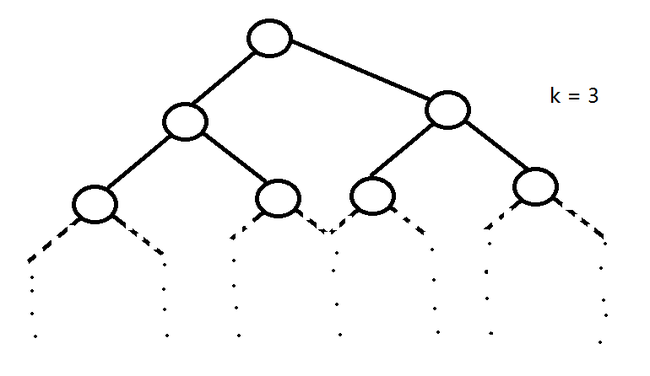
Thus in a red-black tree with n nodes, there is a root-NULL path (the shortest path) with at most log2(n+1) black nodes.
By 4th Invariant : every root-NULL path has black nodes at most log2(n+1)
By 3rd Invariant : every root-NULL path has at most 2log2(n+1) total nodes.
12. Key primitive for balanced search tree : common to all balanced search tree such as AVL, Red-Black, B+, etc. Locally balance subtrees at a node in O(1) time.