1. Basic plan:
a) Shuffle the array.
b) Partition so that, for some j
– entry a[j] is in place
– no larger entry to the left of j
– no smaller entry to the right of j
c) Sort each piece recursively.
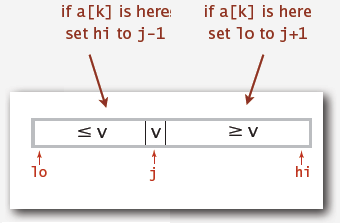
2. Partitioning:
Repeat following steps until i and j pointers cross:
a) Scan i from left to right so long as (a[i] < a[lo]).
b) Scan j from right to left so long as (a[j] > a[lo]).
c) Exchange a[i] with a[j].
When pointers cross.
a) Exchange a[lo] with a[j].
private static int partition(Comparable[] a, int lo, int hi)
{
int i = lo, j = hi+1;
while (true)
{
while (less(a[++i], a[lo]))
if (i == hi) break;
while (less(a[lo], a[--j]))
if (j == lo) break; // this test is redundant
if (i >= j) break;
exch(a, i, j);
}
exch(a, lo, j);
return j;
}
3. Quick Sort Implementation :
public class Quick
{
private static int partition(Comparable[] a, int lo, int hi)
{ /* see previous slide */ }
public static void sort(Comparable[] a)
{
StdRandom.shuffle(a);
sort(a, 0, a.length - 1);
}
private static void sort(Comparable[] a, int lo, int hi)
{
if (hi <= lo) return;
int j = partition(a, lo, hi);
sort(a, lo, j-1);
sort(a, j+1, hi);
}
}
4. Best case: each time the partition element is in the middle of the array to be sorted. Number of compares is ~ N lg N.
5. Worst case: the array to be sorted is already in order ( or in reverse order). Number of compares is ~ ½ N^2 .
6. Proposition: The average number of compares to quicksort an array of N distinct keys is ~ 2N ln N (1.39 N lg N ) and the number of exchanges is ~ ⅓ N ln N. ( 39% more compares than mergesort. But faster than mergesort in practice because of less data movement.)
7. Quick Sort is in-place sorting algorithm and not stable.
8. Improvements:
a) Insertion sort small subarrays.
--Even quicksort has too much overhead for tiny subarrays.
--Cutoff to insertion sort for ≈ 10 items.
--Note: could delay insertion sort until one pass at end.
private static void sort(Comparable[] a, int lo, int hi)
{
if (hi <= lo + CUTOFF - 1)
{
Insertion.sort(a, lo, hi);
return;
}
int j = partition(a, lo, hi);
sort(a, lo, j-1);
sort(a, j+1, hi);
}
b) Median of sample.
--Best choice of pivot item = median.
--Estimate true median by taking median of sample.
--Median-of-3 (random) items.
private static void sort(Comparable[] a, int lo, int hi)
{
if (hi <= lo) return;
int m = medianOf3(a, lo, lo + (hi - lo)/2, hi);
swap(a, lo, m);
int j = partition(a, lo, hi);
sort(a, lo, j-1);
sort(a, j+1, hi);
}
9. The goal of selection problem : Given an array of N items, find the kth largest. Ex. Min (k = 0), max (k = N - 1), median (k = N / 2).
10. Quick Select :
a) Partition array so that:
--Entry a[j] is in place.
--No larger entry to the left of j.
--No smaller entry to the right of j.
b) Repeat in one subarray, depending on j; finished when j equals k.
public static Comparable select(Comparable[] a, int k)
{
StdRandom.shuffle(a);
int lo = 0, hi = a.length - 1;
while (hi > lo)
{
int j = partition(a, lo, hi);
if (j < k) lo = j + 1;
else if (j > k) hi = j - 1;
else return a[k];
}
return a[k];
}
11. Proposition: Quick-select takes linear time on average.
12. Quick-select uses ~ ½ N^2 compares in the worst case. but the random shuffle provides a probabilistic guarantee.
13. If the array to be sorted contains large amount of duplicate keys:
MergeSort : Between ½ N lg N and N lg N compares.
Quicksort: Algorithm goes quadratic unless partitioning stops on equal keys
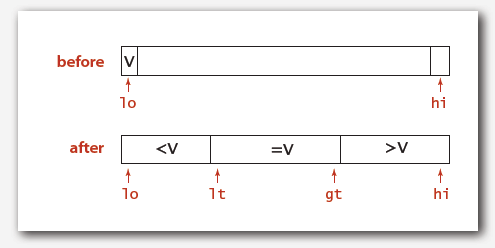
14. 3-way partitioning: Goal--Partition array into 3 parts so that:
a) Entries between lt and gt equal to partition item v.
b) No larger entries to left of lt.
c) No smaller entries to right of gt.
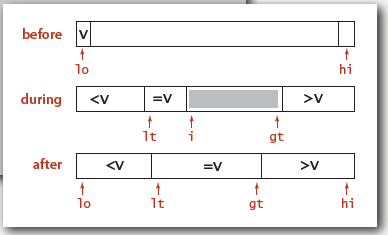
15. Algorithm of 3-way partitioning :
a) Let v be partitioning item a[lo].
b) Scan i from left to right.
– (a[i] < v): exchange a[lt] with a[i]; increment both lt and i
– (a[i] > v): exchange a[gt] with a[i]; decrement gt
– (a[i] == v): increment i
private static void sort(Comparable[] a, int lo, int hi)
{
if (hi <= lo) return;
int lt = lo, gt = hi;
Comparable v = a[lo];
int i = lo;
while (i <= gt)
{
int cmp = a[i].compareTo(v);
if (cmp < 0) exch(a, lt++, i++);
else if (cmp > 0) exch(a, i, gt--);
else i++;
}
sort(a, lo, lt - 1);
sort(a, gt + 1, hi);
}
16. Randomized quicksort with 3-way partitioning reduces running time from linearithmic to linear in broad class of applications.
17. The reason why Java adopt tuned quick sort for primitives and tuned merge sort for objects is that it's assumed that if primitives are used , it means the user cares much about spaces.
18. Tukey's ninther. Median of the median of 3 samples, each of 3 entries.
a) Approximates the median of 9.
b) Uses at most 12 compares.
Better partitioning than random shuffle and less costly.
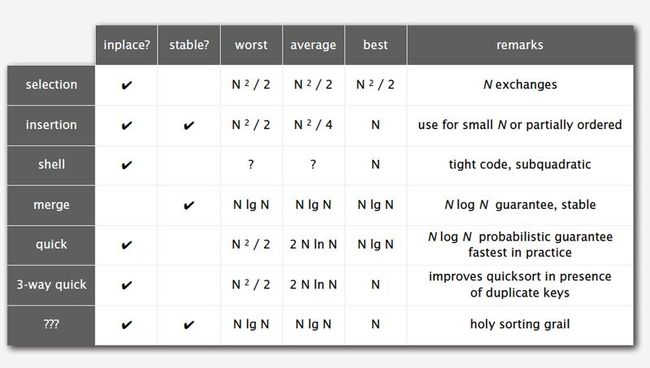
18. Sorting Summary: