主席树/函数式线段树/可持久化线段树

什么是主席树

可持久化数据结构(Persistent data structure)就是利用函数式编程的思想使其支持询问历史版本、同时充分利用它们之间的共同数据来减少时间和空间消耗。

因此可持久化线段树也叫函数式线段树又叫主席树。

 

可持久化数据结构

在算法执行的过程中，会发现在更新一个动态集合时，需要维护其过去的版本。这样的集合称为是可持久的。

实现持久集合的一种方法时每当该集合被修改时，就将其整个的复制下来，但是这种方法会降低执行速度并占用过多的空间。

考虑一个持久集合S。

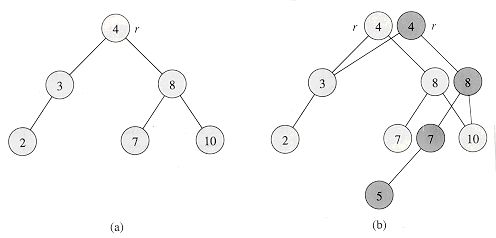
如图所示，对集合的每一个版本维护一个单独的根，在修改数据时，只复制树的一部分。

称之为可持久化数据结构。

 

可持久化线段树

令 T 表示一个结点，它的左儿子是 left(T)，右儿子是 right(T)。

若 T 的范围是 [L,R]，那么 left(T) 的范围是 [L,mid]，right(T) 的范围是 [mid+1,R]。

单点更新

我们要修改一个叶子结点的值，并且不能影响旧版本的结构。

在从根结点递归向下寻找目标结点时，将路径上经过的结点都复制一份。

找到目标结点后，我们新建一个新的叶子结点，使它的值为修改后的版本，并将它的地址返回。

对于一个非叶子结点，它至多只有一个子结点会被修改，那么我们对将要被修改的子结点调用修改函数，那么就得到了它修改后的儿子。

在每一步都向上返回当前结点的地址，使父结点能够接收到修改后的子结点。

在这个过程中，只有对新建的结点的操作，没有对旧版本的数据进行修改。

区间查询

从要查询的版本的根节点开始，像查询普通的线段树那样查询即可。

延迟标记

...

 

区间第K小值问题

有n个数，多次询问一个区间[L,R]中第k小的值是多少。

查询[1,n]中的第K小值

我们先对数据进行离散化，然后按值域建立线段树，线段树中维护某个值域中的元素个数。

在线段树的每个结点上用cnt记录这一个值域中的元素个数。

那么要寻找第K小值，从根结点开始处理，若左儿子中表示的元素个数大于等于K，那么我们递归的处理左儿子，寻找左儿子中第K小的数；

若左儿子中的元素个数小于K，那么第K小的数在右儿子中，我们寻找右儿子中第K-(左儿子中的元素数)小的数。

查询区间[L,R]中的第K小值

我们按照从1到n的顺序依次将数据插入可持久化的线段树中，将会得到n+1个版本的线段树（包括初始化的版本），将其编号为0~n。

可以发现所有版本的线段树都拥有相同的结构，它们同一个位置上的结点的含义都相同。

考虑第i个版本的线段树的结点P，P中储存的值表示[1,i]这个区间中，P结点的值域中所含的元素个数；

假设我们知道了[1,R]区间中P结点的值域中所含的元素个数，也知道[1,L-1]区间中P结点的值域中所包含的元素个数，显然用第一个个数减去第二个个数，就可以得到[L,R]区间中的元素个数。

因此我们对于一个查询[L,R]，同步考虑两个根root[L-1]与root[R]，用它们同一个位置的结点的差值就表示了区间[L,R]中的元素个数，利用这个性质，从两个根节点，向左右儿子中递归的查找第K小数即可。 

POJ 2104 K-th Number (HDU 2665)

注意可持久化数据结构的内存开销非常大，因此要注意尽可能的减少不必要的空间开支。

 1 const int maxn=100001;

 2 struct Node{

 3     int ls,rs;

 4     int cnt;

 5 }tr[maxn*20];

 6 int cur,rt[maxn];

 7 void init(){

 8     cur=0;

 9 }

10 inline void push_up(int o){

11     tr[o].cnt=tr[tr[o].ls].cnt+tr[tr[o].rs].cnt;

12 }

13 int build(int l,int r){

14     int k=cur++;

15     if (l==r) {

16         tr[k].cnt=0;

17         return k;

18     }

19     int mid=(l+r)>>1;

20     tr[k].ls=build(l,mid);

21     tr[k].rs=build(mid+1,r);

22     push_up(k);

23     return k;

24 }

25 int update(int o,int l,int r,int pos,int val){

26     int k=cur++;

27     tr[k]=tr[o];

28     if (l==pos&&r==pos){

29         tr[k].cnt+=val;

30         return k;

31     }

32     int mid=(l+r)>>1;

33     if (pos<=mid) tr[k].ls=update(tr[o].ls,l,mid,pos,val);

34     else tr[k].rs=update(tr[o].rs,mid+1,r,pos,val);

35     push_up(k);

36     return k;

37 }

38 int query(int l,int r,int o,int v,int kth){

39     if (l==r) return l;

40     int mid=(l+r)>>1;

41     int res=tr[tr[v].ls].cnt-tr[tr[o].ls].cnt;

42     if (kth<=res) return query(l,mid,tr[o].ls,tr[v].ls,kth);

43     else return query(mid+1,r,tr[o].rs,tr[v].rs,kth-res);

44 }

主席树

 

常数优化的技巧

一种在常数上减小内存消耗的方法：

插入值时候先不要一次新建到底，能留住就留住，等到需要访问子节点时候再建下去。

这样理论内存复杂度依然是O(Nlg^2N)，但因为实际上很多结点在查询时候根本没用到，所以内存能少用一些。

 

动态第K小值

每一棵线段树是维护每一个序列前缀的值在任意区间的个数，如果还是按照静态的来做的话，那么每一次修改都要遍历O(n)棵树，时间就是O(2*M*nlogn)->TLE。

考虑到前缀和，我们通过树状数组来优化，即树状数组套主席树，每个节点都对应一棵主席树，那么修改操作就只要修改logn棵树，O(nlognlogn+Mlognlogn)时间是可以的，但是直接建树要nlogn*logn（10^7）会MLE。

我们发现对于静态的建树我们只要nlogn个节点就可以了，而且对于修改操作，只是修改M次，每次改变俩个值（减去原先的，加上现在的）也就是说如果把所有初值都插入到树状数组里是不值得的，所以我们分两部分来做，所有初值按照静态来建，内存O(nlogn)，而修改部分保存在树状数组中，每次修改logn棵树，每次插入增加logn个节点O(M*logn*logn+nlogn)。

 

可用主席树解决的问题

 

POJ 2104 K-th Number

入门题，求区间第K小数。

 1 #include <iostream>

 2 #include <cstdio>

 3 #include <cstring>

 4 #include <algorithm>

 5 using namespace std;

 6 const int maxn=100001;

 7 struct Node{

 8     int ls,rs;

 9     int cnt;

10 }tr[maxn*20];

11 int cur,rt[maxn];

12 void init(){

13     cur=0;

14 }

15 inline void push_up(int o){

16     tr[o].cnt=tr[tr[o].ls].cnt+tr[tr[o].rs].cnt;

17 }

18 int build(int l,int r){

19     int k=cur++;

20     if (l==r) {

21         tr[k].cnt=0;

22         return k;

23     }

24     int mid=(l+r)>>1;

25     tr[k].ls=build(l,mid);

26     tr[k].rs=build(mid+1,r);

27     push_up(k);

28     return k;

29 }

30 int update(int o,int l,int r,int pos,int val){

31     int k=cur++;

32     tr[k]=tr[o];

33     if (l==pos&&r==pos){

34         tr[k].cnt+=val;

35         return k;

36     }

37     int mid=(l+r)>>1;

38     if (pos<=mid) tr[k].ls=update(tr[o].ls,l,mid,pos,val);

39     else tr[k].rs=update(tr[o].rs,mid+1,r,pos,val);

40     push_up(k);

41     return k;

42 }

43 int query(int l,int r,int o,int v,int kth){

44     if (l==r) return l;

45     int mid=(l+r)>>1;

46     int res=tr[tr[v].ls].cnt-tr[tr[o].ls].cnt;

47     if (kth<=res) return query(l,mid,tr[o].ls,tr[v].ls,kth);

48     else return query(mid+1,r,tr[o].rs,tr[v].rs,kth-res);

49 }

50 int b[maxn];

51 int sortb[maxn];

52 int main()

53 {

54     int n,m;

55     int T;

56     //scanf("%d",&T);

57     //while (T--){

58     while (~scanf("%d%d",&n,&m)){

59         init();

60         for (int i=1;i<=n;i++){

61             scanf("%d",&b[i]);

62             sortb[i]=b[i];

63         }

64         sort(sortb+1,sortb+1+n);

65         int cnt=1;

66         for (int i=2;i<=n;i++){

67             if (sortb[i]!=sortb[cnt]){

68                 sortb[++cnt]=sortb[i];

69             }

70         }

71         rt[0]=build(1,cnt);

72         for (int i=1;i<=n;i++){

73             int p=lower_bound(sortb+1,sortb+cnt+1,b[i])-sortb;

74             rt[i]=update(rt[i-1],1,cnt,p,1);

75         }

76         for (int i=0;i<m;i++){

77             int a,b,k;

78             scanf("%d%d%d",&a,&b,&k);

79             int idx=query(1,cnt,rt[a-1],rt[b],k);

80             printf("%d\n",sortb[idx]);

81         }

82     }

83     return 0;

84 }

POJ 2104 K-th Number

 

SPOJ 3267 D-query

求区间内不重复的数的个数。

扫描数列建立可持久化线段树，第i个数若第一次出现，则在线段树中的位置i加1；若不是第一次出现，将上次出现的位置减1，在本次位置加1。

对于每个询问的区间 [L,R]，在第R个版本上的线段树只有前R个数，在线段树上查询位置L，对经过的区间中的和进行累计即可。

 1 #include <iostream>

 2 #include <cstdio>

 3 #include <cstring>

 4 #include <algorithm>

 5 #include <map>

 6 using namespace std;

 7 const int maxn=100001;

 8 struct Node{

 9     int ls,rs;

10     int cnt;

11 }tr[maxn*20];

12 int cur,rt[maxn];

13 void init(){

14     cur=0;

15 }

16 inline void push_up(int o){

17     tr[o].cnt=tr[tr[o].ls].cnt+tr[tr[o].rs].cnt;

18 }

19 int build(int l,int r){

20     int k=cur++;

21     if (l==r) {

22         tr[k].cnt=0;

23         return k;

24     }

25     int mid=(l+r)>>1;

26     tr[k].ls=build(l,mid);

27     tr[k].rs=build(mid+1,r);

28     push_up(k);

29     return k;

30 }

31 int update(int o,int l,int r,int pos,int val){

32     int k=cur++;

33     tr[k]=tr[o];

34     if (l==pos&&r==pos){

35         tr[k].cnt+=val;

36         return k;

37     }

38     int mid=(l+r)>>1;

39     if (pos<=mid) tr[k].ls=update(tr[o].ls,l,mid,pos,val);

40     else tr[k].rs=update(tr[o].rs,mid+1,r,pos,val);

41     push_up(k);

42     return k;

43 }

44 int query(int l,int r,int o,int pos){

45     if (l==r) return tr[o].cnt;

46     int mid=(l+r)>>1;

47     if (pos<=mid) return tr[tr[o].rs].cnt+query(l,mid,tr[o].ls,pos);

48     else return query(mid+1,r,tr[o].rs,pos);

49 }

50 int b[maxn];

51 map<int,int> mp;

52 int main()

53 {

54     int n,m;

55     //int T;

56     //scanf("%d",&T);

57     //while (T--){

58     while (~scanf("%d",&n)){

59         mp.clear();

60         init();

61         for (int i=1;i<=n;i++){

62             scanf("%d",&b[i]);

63         }

64         rt[0]=build(1,n);

65         for (int i=1;i<=n;i++){

66             if (mp.find(b[i])==mp.end()){

67                 mp[b[i]]=i;

68                 rt[i]=update(rt[i-1],1,n,i,1);

69             }

70             else{

71                 int tmp=update(rt[i-1],1,n,mp[b[i]],-1);

72                 rt[i]=update(tmp,1,n,i,1);

73             }

74             mp[b[i]]=i;

75         }

76         scanf("%d",&m);

77         for (int i=0;i<m;i++){

78             int a,b;

79             scanf("%d%d",&a,&b);

80             int ans=query(1,n,rt[b],a);

81             printf("%d\n",ans);

82         }

83     }

84     return 0;

85 }

SPOJ 3267 D-query