2-6基础算法-快速幂/倍增/构造

一.快速幂

快速幂算法是一种高效计算幂a^b的方法，特别是当b非常大时。它基于幂运算的性质，将幂运算分解成一系列的平方操作，以此减少乘法的次数。算法的核心在于将指数b表示为二进制形式，并利用二进制位来决定何时将当前的底数的幂乘入结果中。

普通的快速幂算法

#include 
#include 
using namespace std;
long long fastPower(long long base, long long power) {
	long long result = 1;
	while (power > 0) {
		if (power % 2 == 1) {
			result *= base;
		}
		base *= base;
		power /= 2;
	}
	return result;
}
int main() {
	long long base, power;
	cin >> base >> power;
	cout << fastPower(base, power);
}

为了适用于大数运算，提高效率，引入了位运算和模运算
位运算：比乘除法和模运算更快。
模运算：在每次乘法后进行，避免了大整数的处理和溢出的问题。

#include 
#include 
using namespace std;
#define mod 998244353  //固定数
long long fastPower(long long base, long long power) {
	long long result = 1;
	while (power > 0) {
		if (power&1) { //power % 2 == 1
			result *= base% mod;
		}
		base *= base% mod;
		power >>= 1;//右移一位，相当于÷2，即power /= 2;
	}
	return result;
}
int main() {
	long long base, power;
	cin >> base >> power;
	cout << fastPower(base, power);
}

[例] 快速幂

评测系统

#include 
#include 
using namespace std;
long long fastPower(long long base, long long power, long long k) {
	long long result = 1;
	while (power > 0) {
		if (power & 1) {
			result = result * base % k;
		}
		base = base * base % k;
		power >>= 1;
	}
	return result;
}
int main() {
	long long b, p, k;
	cin >> b >> p >> k;
	long long s = fastPower(b, p, k);
	cout << s;
}

二.倍增

倍增算法是一种用于解决各种问题的通用技术，例如在计算斐波那契数列、找到图中节点的祖先或者处理区间查询问题（如最小值或最大值）时。其基本思想是通过重复倍增一个数或者序列的长度，从而以对数时间解决问题。例如，在求解LCA（最近公共祖先）问题时，倍增算法可以在预处理阶段通过倍增跳跃来快速移动到任意节点的不同层级的祖先节点。

[例1] 最近公共祖先LCA查询

评测系统

分析：
（1）预处理
①使用DFS从根节点开始变量，计算每个结点的所有祖先
②使用数组parent[node][i]存储结点node的第2ⁱ个祖先，parent[node][0]就是结点node的父节点，parent[node][1]就是node的第2个祖先
③递推式parent[node][i]=parent[parent[node][i-1]][i-1] //两个i-1就是i
（2）查询
为了找到两个结点u和v的最低公共祖先，若u的深度≥v，我们将u的深度提升至与v相同，若提升后的u与v是同一结点，则该结点就是他们的最低公共祖先，否则同时提升二者的深度，直到他们有相同的第2ⁱ个祖先为止

例如查找第1248个祖先，1248二进制表示为10011100000
即1248=2¹⁰+2⁷+2⁶+2⁵
即从node向上跳2¹⁰步，再跳2⁷，再跳2⁶，再跳2⁵
即任意一个数都可以通过向上跳2ⁱ来表示

#include 
#include 
#include 
using namespace std;
const int MAXN = 1e5 + 5;//节点数量的上限
const int MAXLOG = 20;//最大深度,2^20>1e5
vector<int> tree[MAXN];//tree[i]存储了所有直接连接到节点i的子节点的列表，即树的邻接表表示
int parent[MAXN][MAXLOG];
int depth[MAXN];//每个节点在树中的深度
void dfs(int node, int prev) { //遍历树并填充 parent 和 depth 数组
	for (int i = 1; i < MAXLOG; i++) {
		parent[node][i] = parent[parent[node][i - 1]][i - 1];
	}
	for (int child : tree[node]) {  //递归处理子节点
		if (child != prev) {
			depth[child] = depth[node] + 1;
			parent[child][0] = node;
			dfs(child, node);
		}
	}
}
int lca(int u, int v) {
	if (depth[u] < depth[v]) swap(u, v);//确保u更深
	for (int i = MAXLOG - 1; i >= 0; i--) { //向上提升u
		if (depth[u] - (1 << i) >= depth[v]) { //1<
			u = parent[u][i];
		}
	}
	if (u == v)
		return u;
	for (int i = MAXLOG - 1; i >= 0; i--) {
		if (parent[u][i] != parent[v][i]) {
			u = parent[u][i];
			v = parent[v][i];
		}
	}
	return parent[u][0];
}
int main() {
	int N;
	cin >> N;
	for (int i = 1; i < N; i++) {
		int u, v;
		cin >> u >> v;
		tree[u].push_back(v);
		tree[v].push_back(u);
	}
	dfs(1, -1);
	int Q;
	cin >> Q;
	while (Q--) {
		int a, b;
		cin >> a >> b;
		cout << lca(a, b) << endl;
	}
	return 0;
}

[例2] 如今仍是遥远的理想之城1

对于小数据

#include 
#include 
using namespace std;
const int N = 2e5 + 5;
int main() {
	int n, k;
	cin >> n >> k;
	long long a[N];
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	long long position = 1;
	while(k--) {
		position = a[position];
	}
	cout << position;
}

对于大数据
需要移除重复的循环
例如
第 1 次传送：从 1 到 2
第 2 次传送：从 2 到 3
第 3 次传送：从 3 到 4
第 4 次传送：从 4 到 2
在第 4 次传送时，我们回到了传送阵 2，这里形成了一个循环：2 -> 3 -> 4 -> 2,这个循环会一直重复,循环长度为3
可以看出，当k足够大时,若pre=1说明一定没有节点能跳转到当前结点。若pre=2，当k足够大时一定有能跳转过来的，也就一定能出现循环

#include 
#include 
using namespace std;
const int N = 2e5 + 5;
int main() {
	long long n, k;
	cin >> n >> k;
	long long a[N], pre[N] = { 0 };//pre[position]表示访问到position时总的传送次数【这里必须初始化为0】
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	long long position = 1;
	long long num = 1;//num表示总传送次数
	while (k--) {
		position = a[position];
		if (pre[position])
			k = k % (num - pre[position]);//num-1-pre[position]表示这个循环的长度
		pre[position] = num++;

	}
	cout << position;
}

注：局部变量不会自动初始化为零，全局变量会初始化为0。在main函数内long long a[N], pre[N]时必须初始化为0，或者直接在全局定义。

[例3] 数的变换

分析：F[i][j]表示A初始为i时，经过2^j次变换的值，其中2⁰=1次变换表示进行一次变化，即输出A/B+C；2¹=2表示两次变换，即将A/B+C作为新的A，放入A/B+C中，输出结果

例如：
A = 10, B = 2, C = 1, D = 5
F[i][0]表示A=i时，即i/b+c的值，通过遍历i的所有可能，以此作为第0列的值，即初始化过程。由于A不断变为A/B+C，所以A的最大取值为max(1e5,A/B+C的大小)=max(1e5,2e5)=2e5，即F的最大行数
以下是第0列的初始化过程

for (int i = 0; i <= 200000; i++) {  //初始化
		F[i][0] = i / b + c;
}

然后我们按列更新
更新F[0][1]时，表示A=0经过2¹=2次变换的结果，具体的变化过程为A=0→A=1（一次变换）→A=1（两次变换）

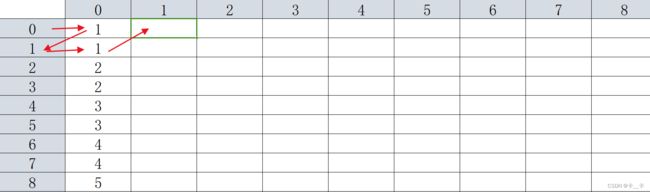
更新F[3][1]同样

即对第一列所有的更新，我们都是把F[i][0]作为新的行，找到第0列对应的值（即一次变换）

for (int i = 0; i <= 200000; i++) {
	F[i][1] = F[F[i][0]],0];
}

更新F[18][2]时，从A=18起经过了4次变换，得到了3

显然，我们从F[18][2]的左侧F[18][1]=6开始，进行两次变换（标号3和4）更快得到了答案
更显然的，A=6进行两次变化，可以直接从表格中的F[6][1]得到（注意1是2¹）
我们据此更新第二列，以当前行前一列的值（6）作为行，直接找到该行（6这一行）前一列（第1列）的值（3），即为结果

for (int i = 0; i <= 200000; i++) {
	F[i][2] = F[F[i][1]],1];
}

对于第j列的更新，按照同样的逻辑，我们有

for (int i = 0; i <= 200000; i++) {
	F[i][j] = F[F[i][j-1]],j-1];
}

再遍历所有的j，我们有

for (int j = 1; j <= 30; j++) {
	for (int i = 0; i <= 200000; i++) {
		F[i][j] = F[F[i][j - 1]][j - 1];
	}
}

j表示进行2^j次变换，2³⁰>1e9=maxQ（查询次数的最大值）

以上过程是倍增的重要思想

当A=3时，1左移3位就是1000，视为二进制，对应的十进制是8，即2³，可视为F[i][j]的j=3
当A=8时，1左移8位就是100000000，视为二进制，对应的十进制是256，即2⁸，可视为F[i][j]的j=8
可以看出，A的值=1左移位数=j的值
而j的范围很小，是从0到30，我们遍历j就相当于遍历了A
1左移j位得到的这个二进制数中只会有一个1，我们将查询次数Q也写为二进制，二者相与，若结果为1，说明两个二进制数一定完全相同，即此时Q的二进制中也只有一个1，而这个1所在的位置可以通过1< 因此，通过遍历j，当相与为1时，我们可以直接在F数组中找到F[A][j]

for (int j = 0; j <= 30; j++) {
	if ((1 << j) & q) {
		answer = F[A][j];
		break;
	}
}

因此，本题的求解代码为

#include 
#include 
using namespace std;
const int N = 2e5 + 5, M = 30 + 5;
int main() {
	long long a, b, c, q;
	long long F[N][M];
	cin >> a >> b >> c >> q;
	if (b == 1) { //特殊情况
		cout << a + q * c;
		return 0;
	}
	for (int i = 0; i <= 200000; i++) {
		F[i][0] = i / b + c;
	}
	for (int j = 1; j <= 30; j++) {
		for (int i = 0; i <= 200000; i++) {
			F[i][j] = F[F[i][j - 1]][j - 1];
		}
	}
	for (int j = 0; j <= 30; j++) {
		if ((1 << j) & q) {
			a = F[a][j];
			break;
		}
	}
	cout << a;
}

三.构造

通过观察问题的结构和规律，找到一种通用的方法或模式，使得在问题规模增大时，依然能够高效地得到答案。

1.小浩的ABC


评测系统

分析：
A*B+C>=2，若X<2，无解
若X<=10⁶+1，则B=C=1,A=X-1。此时字典序一定是最小的
若X>10⁶+1，为了让B更小，应该A尽可能大，即A=10⁶
若A、C都是10⁶，那么X一定是10⁶的整数倍，即有X%10⁶=0
若X不是10⁶的整数倍，说明C一定不是10⁶，设X=1e7+2
A=1e6，B=9，C=1e6，不满足
A=1e6，B=10，C=2，满足，显然B=X/A，C=X%A

#include 
#include 
using namespace std;
int main() {
	long long T, A, B, C;
	cin >> T;
	while (T--) {
		long long X;
		cin >> X;
		if (X < 2) {
			cout << "-1" << endl;
		}
		else {
			if (X <= 1e6 + 1) {
				B = 1, C = 1, A = X - 1;
			}
			else {
				A = 1e6;
				if (X % 1000000 == 0) {
					C = 1e6, B = (X - C) / A;
				}
				else {
					B = X / 1000000;
					C = X % 1000000;
				}
			}
			cout << A << " " << B << " " << C << endl;
		}
	}
}

2.小新的质数序列挑战


评测系统

分析：质数：2、3、5、7、11
A和B任一个小于2都失败
每一个偶数都能由多个2组成，每一个奇数都能由1个3和多个2组成
因此输出只能为0或1
若AB都是偶数，输出一定为0
若AB相等，输出一定为0
其他情况需要具体分析
如一奇一偶
27和24，由9个3和8个3组成，输出为0
3和5，由3和2 3组成，输出为1
所以可以查看AB（大于1的）公因数，若有，则输出为0，否则为1
此方法也涵盖了都是偶数和两数相等的情况

#include 
#include 
using namespace std;
long long f(long long a, long long b) { //求最大公因数
	while (b) {
		long long temp = b;
		b = a % b;
		a = temp;
	}
	return a;
}
int main() {
	int T;
	cin >> T;
	long long A, B;
	while (T--) {
		cin >> A >> B;
		if (A < 2 || B < 2) {
			cout << "-1" << endl;
		}
		else {
			if (f(A, B) > 1) {
				cout << "0" << endl;
			}
			else
				cout << "1" << endl;
		}
	}
}

3.小蓝找答案

评测系统

【本题分析与注释仅供参考】

分析：
①假设3个字符串的长度分别为1，2，3
s1:a
s2长度为2，aa满足
s3长度为3，aaa满足
因此长度|s_i|<长度|s_i+1|，显然没有产生进位，那么s_i就是s_i+1的前缀。所以s_i+1是由s_i向后补字符集中最小的字母，直到长度等于s_i+1

②假设3个字符串的长度分别为3，2，1
s1:aaa
s2长度为2，将s1的长度变为2（即截尾），得到aa，显然不满足，最后一位+1得到ab，满足
s3长度为1，将s2的长度变为1（截尾），得到a，显然不满足，最后一位+1得到b，满足
因此长度|s_i|≥长度|s_i+1|，一定产生了进位，具体来说是s_i截尾后的最后一位加1得到的。

③假设3个字符串的长度分别为3，2，2（这里k=2）
s1:aaa
s2长度为2，将s1的长度变为2（即截尾），得到aa，显然不满足，最后一位+1得到ab，满足
s3长度为2，将s2的长度变为2（不变），得到ab，显然不满足，最后一位+1得到了ac，这时c>字符集中最小的字母+1，需要再次进位（即进位到前一位），ac变为ba

④假设s2为abc（这里k=3）
s3长度为3，将s2的长度变为3（不变），得到abc，显然不满足，最后一位+1得到abd，此时d>字符集中最小的字母+2，需要再次进位（即进位到前一位），abd变为aca
因此，当某一位>字符集中最小的字母+k-1时，就产生了进位
或者更通用的，当某一位+1后>字符集中最小的字母+k时，就产生了进位

⑤假设4个字符串的长度分别为3，1，2，2
s1:aaa
s2长度为1，将s1的长度变为1（截尾），得到a，显然不满足，最后一位+1得到b，满足
s3长度为2，将s2作为前缀，后面补字符集中最小的字母至与s3等长，得到bb，满足
s4长度为2，将s2的长度变为2（不变），得到bb，显然不满足，最后一位+1得到了bc；这时c>字符集中最小的字母+1，需要再次进位（即进位到前一位），bc变为ca；这时c>字符集中最小的字母+1，需要再次进位（即进位到前一位），ca变为aaa，超出长度。即第一位产生进位就是不合法。

我们假设字符集的大小为k，使用二分去找最小的合法字符集的大小，并验证二分出来的k是否合法

最终代码

#include 
#include 
using namespace std;
const int N = 2e5 + 5;
int s[N];
int n;
struct node {
    int pos;//字符串长度
    int num;//长度为pos的字符串产生的进位次数
}stk[N];//栈
int top;//栈顶指针
void insert(int v, int mid) {//处理进位
    while (top > 1 && stk[top].pos > v)//截尾。或者说当前长度的进位信息我们当前不需要考虑,可以移除
        top--;
    if (stk[top].pos == v)//如果二者长度相等
        stk[top].num++;//直接复制过来,最后一位+1。即产生进位次数+1
    else//如果长度不相等,新信息压入栈
        stk[++top] = { v,1 };//进位次数初始化为1
    if (top > 1 && stk[top].num == mid)//若某个长度的字符串的进位次数≥mid,需要向前进位。如aa/ab两次进位==mid=2,此时需要向前进位变成ba
        insert(v - 1, mid);
}
int check(int mid) {//验证给定的字符集大小mid是否足够用来构造出满足条件的字符串序列
    top = 1;
    stk[top] = { 0,0 };
    for (int i = 1; i < n; i++) {
        if (s[i + 1] <= s[i]) //一定有进位
            insert(s[i + 1], mid);
    }
    return stk[1].num;//返回第一个位置上的进位,为0表示没有进位,即合法
}
int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> s[i];
    }
    int num = 0;
    for (int i = 1; i < n; i++) {
        if (s[i + 1] > s[i])
            num++;
    }
    if (num == n - 1) { //如果从第二个起每一个都能通过"补齐"实现，则字符集中只有a
        cout << "1";
        return 0;
    }
    //补不了,使用二分找k
    int left = 2, right = 2e5 + 5;
    int ans = 0;
    while (left + 1 != right) {
        int mid = (left + right) / 2;
        if (check(mid) == 0)
            right = mid;
        else
            left = mid;
    }
    if (check(left) == 0)
        cout << left;
    else
        cout << right;
}

一些具体的分析：
①假设我们有一个字符串长度序列 [4, 3, 2, 1]，并且我们正在按序处理这些字符串的长度。我们将关注栈中的变化，特别是在 top-- 过程中栈的状态。

while (top > 1 && stk[top].pos > v)//当前长度更小
	top--;

处理长度4:
假设栈初始为 [{0, 0}]。
长度4是序列中的第一个元素，因此不需要进位操作。栈状态不变。

处理长度3:
当我们开始处理长度3的字符串时，由于它小于4，我们需要在长度3上进行一次进位操作。
栈变为 [{0, 0}, {3, 1}]。

处理长度2:
现在我们处理长度2的字符串。在这里，长度为3的进位记录（即 {3, 1}）不再相关，因为我们现在关注的是长度2。
执行 top–，栈中长度为3的记录被移除，栈变回 [{0, 0}]。
然后，我们在长度2上进行进位操作，栈变为 [{0, 0}, {2, 1}]。

处理长度1:
接下来是长度1的字符串。同样，长度为2的记录（即 {2, 1}）现在不再相关。
执行 top–，移除长度为2的记录，栈变回 [{0, 0}]。
在长度1上进行
进位操作，栈变为 [{0, 0}, {1, 1}]。

在 top-- 的过程中，栈中存储的是之前处理的不同长度字符串的进位记录。每当我们转向处理一个更短的字符串时，所有比这个新长度长的字符串的进位记录都变得不再相关，因此需要被移除。这些进位记录反映了在之前长度上的字符集使用情况和进位情况。

②假设有一个字符串长度序列 [3, 2, 2, 1]，我们考虑如何处理这些长度并记录进位信息：

if (stk[top].pos == v)//如果二者长度相等
	stk[top].num++;

处理长度3: 不需要进位，假设栈状态是 [{0, 0}]。
处理长度2: 第一次出现长度2，进行一次进位操作。栈状态变为 [{0, 0}, {2, 1}]。
再次处理长度2: 当再次遇到长度2时，栈顶元素已经是 {2, 1}。这时，这行代码 stk[top].num++ 会执行，表示在长度2上又发生了一次进位。栈状态更新为[{0, 0}, {2, 2}]，意味着在长度为2的字符串上发生了两次进位操作。

③当字符串长度再次变为之前处理过的长度时，确保 num 是累加的
示例分析
考虑序列 [3, 2, 2, 1, 2, 2]：
处理长度 3，不涉及进位操作。
处理第一个长度 2，进行一次进位操作，栈变为 [{2, 1}]。
处理第二个长度 2，再次进位，栈更新为 [{2, 2}]。
处理长度 1，由于这比 2 小，栈清除长度 2 的记录，变回 [{0, 0}]，然后为 1 添加进位记录，变为 [{1, 1}]。
再次处理长度 2，由于栈中没有长度 2 的记录，会添加一个新的进位记录，栈变为 [{1, 1}, {2, 1}]。
处理另一个长度 2，找到栈中的 {2, 1}记录，然后将其num增加，栈更新为[{1, 1}, {2, 2}]。
虽然top–的过程删除了部分数据，但num的更新过程是基于当前字符串长度更新的，也能实现累加的效果。

4.小蓝的无限集

分析：
若第一次计算1*a，得到的通式为n=a^x+by （其中xy为任意满足要求的整数）
若第一次计算x+b，得到的通式为n=(1+b)* a^x+by=b*(a^x+y)+a^x
我们可以令x=0，若b%(n-1)==0，则n一定在无限集中
上述条件不满足且a=1，则n一定不在无限集中
此外，根据通式有
n-a^x=by
n-a^x=b*(a^x+y)
我们可以遍历x，计算n-a^x，若b能够将其整除，则n一定在无限集中

#include 
#include 
using namespace std;
int main() {
    int t;
    cin >> t;
    int a, b, n;
    while (t--) {
        cin >> a >> b >> n;
        if ((n - 1) % b == 0) {
            cout << "Yes" << endl;
            continue;
        }
        else if (a == 1) {
            cout << "No" << endl;
            continue;
        }
        long long res = 1;
        bool flag = 0;
        while (res < n) {
            res *= a;
            if (res > n)
                break;
            else if (res == n) {
                cout << "Yes" << endl;
                flag = 1;
                break;
            }
            else if ((n - res) % b == 0) {
                cout << "Yes" << endl;
                flag = 1;
                break;
            }
        }
        if (flag == 1)
            continue;
        cout << "No" << endl;
    }
}