MIT_线性代数笔记：第 34 讲 总复习

本讲为线性代数课程总复习，复习的方法就是做往年试题。

试题1

1）已知 Ax= [ 1 0 0 ] \begin{bmatrix} 1\\0\\0 \end{bmatrix} ​100​ ​ 无解，Ax= [ 0 1 0 ] \begin{bmatrix} 0\\1\\0 \end{bmatrix} ​010​ ​仅有一解。

a）这个矩阵为 m x n 矩阵，秩为 r，那么 m 是多少？r？

答：m=3。Ax= [ 1 0 0 ] \begin{bmatrix} 1\\0\\0 \end{bmatrix} ​100​ ​无解,说明 r小于m，Ax= [ 0 1 0 ] \begin{bmatrix} 0\\1\\0 \end{bmatrix} ​010​ ​仅有一解,说明矩阵零空间只有零向量，所以 r=n。例如 A= [ 0 1 0 ] \begin{bmatrix} 0\\1\\0 \end{bmatrix} ​010​ ​ 或者 A= [ 0 0 1 0 0 1 ] \begin{bmatrix} 0&0\\1&0\\0&1 \end{bmatrix} ​010​001​ ​。

知识点：

b）判断 $det(A^{T}A)=det(A{A}^T)$是否成立？
答：不成立。可以看下面两题的答案，分别是可逆和不可逆的矩阵。需要注意的是：只有当矩阵是方阵时，才有行列式的的乘积等于乘积的行列式。

c）$A^{T}A$是否可逆？
答：可逆，矩阵 A 列满秩 r=n，因此 $A^{T}A$ 可逆。

d）$A{A}^T$是否正定？
答：否，不满秩，不可能是正定矩阵。

e）A^Ty=c，证明对于任意右侧向量至少有一个解。
答：矩阵 $A^T$为 n x 3 矩阵，行满秩，矩阵$A^T$的零空间维数为 3-n，方程有无穷多解。

试题2

2）已知矩阵 $A=\left[\begin{array}{ccc}{v}_1& v_2& v_3\end{array}\right]$
a）求解 $Ax=v_1-v_2+v_3$

答：x= [ 1 − 1 1 ] \begin{bmatrix} 1\\-1\\1 \end{bmatrix} ​1−11​ ​

b）若 $v_1-v_2+v_3=0$，则上一题的解是否不唯一？
答：列向量线性相关，零空间有非零向量，Ax=0 解不唯一。

c）若 $v_1，v_2和v_3$为标准正交，求 $v_1，v_2$线性组合距离 $v_3$最近？
答：原点。

试题3

3）已知 Markov 矩阵 A = [ 0.2 0.4 0.3 0.4 0.2 0.3 0.4 0.4 0.4 ] A=\begin{bmatrix} 0.2& 0.4& 0.3\\0.4&0.2& 0.3\\0.4&0.4& 0.4 \end{bmatrix} A= ​0.20.40.4​0.40.20.4​0.30.30.4​ ​
a）特征值？
答：列1+列2=2 x 列3，所以矩阵为奇异阵，有一个特征值${\lambda }_1=0$。Markov 矩阵还有一个特征值${\lambda }_2=1$，从迹可知最后一个特征值为${\lambda }_3=-0.2$。

b） u k = A k [ 0 10 0 ] u_k=A^k\begin{bmatrix} 0\\10\\0 \end{bmatrix} uk​=Ak ​0100​ ​，求 k 步之后的状态？当 k 趋近于无穷时的状态？

答：$uk=c_1{\lambda }_1^k{x}_1+c_2{\lambda }_2^k{x}_2+c_3{\lambda }_3^k{x}_3$。代入特征值可知，当 k 趋近于无穷时，只剩下 $c_2{x}_2$。求解矩阵的特征向量

$x_2$，得到 x 2 = [ 3 3 4 ] x_2=\begin{bmatrix} 3\\3\\4 \end{bmatrix} x2​= ​334​ ​。$u_0$引入 10 个人（Markov 矩阵可以当作人口流动模型来看），并且最终的分配比例为 3:3:4，所以不用逐个求解特征向量和 c，可得 u k = [ 3 3 4 ] u_k=\begin{bmatrix} 3\\3\\4 \end{bmatrix} uk​= ​334​ ​。

试题4

4）求符合题目要求的 2 x 2 矩阵。

a）投影到 $a=\left[\begin{array}{c}4\\ -3\end{array}\right]$ 所在直线的投影矩阵。
答：$$P=\frac{a{a}^T}{a^{T}a}=\frac{1}{25}\left[\begin{array}{cc}16& -12\\ -12& 9\end{array}\right]$$

b）矩阵具有特征值 0 和 3，对应的特征向量分别为 $\left[\begin{array}{c}1\\ 2\end{array}\right]$和 $\left[\begin{array}{c}2\\ 1\end{array}\right]$。

答：$A=\left[\begin{array}{cc}1& 2\\ 2& 1\end{array}\right]\left[\begin{array}{cc}0& 0\\ 0& 3\end{array}\right]{\left[\begin{array}{cc}1& 2\\ 2& 1\end{array}\right]}^{-1}$

c）矩阵 A 不能分解为 $B^{T}B$。
答：给出一个不对称矩阵就可以了。

d）矩阵有正交的特征向量，但是非对称。
答：反对称矩阵或者在复数域上有正交特征向量的其它矩阵。

试题5

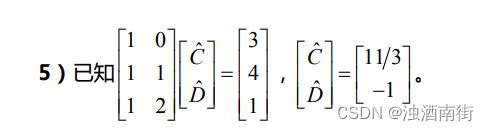
a）求投影 p。
答： p = 11 / 3 [ 1 1 1 ] − 1 [ 0 1 2 ] = [ 11 3 8 3 5 3 ] p=11/3\begin{bmatrix} 1\\1\\1 \end{bmatrix} -1\begin{bmatrix} 0\\1\\2 \end{bmatrix} =\begin{bmatrix} \frac{11}{3}\\\frac{8}{3}\\\frac{5}{3}\end{bmatrix} p=11/3 ​111​ ​−1 ​012​ ​= ​311​38​35​​ ​